BPR(Bayesian Personalized Ranking from Implicit Feedback)
12 Jul 2021 | RecommendSummary
- 대부분의 추천시스템은 missing value에 대해 negative feedback으로 다룸.
- 이는 missing value가 미래에 유저가 선호하는 아이템이 될 수도 있고, 아직 마주치지 못해서 missing value인 상태일 수도 있는데, 이러한 가능성을 배제하고 단순히 이러한 아이템들을 모두 다 negative로만 학습하게 함.
- 따라서 본 논문에선 이를 해결하기 위해 ranking을 고려한 데이터셋을 제안함.
- 또한 논문 타이틀에 적혀 있듯 Bayesian을 사용하여 MAP를 통해 유저의 선호 정보를 잘 나타내줄 수 있는 파라미터를 추정함.
ranking에 대해 조금 더 얘기해보자면, 기존의 추천시스템은 단순히 유저가 아이템을 ‘선택’ 했는지 여부를 예측하도록 최적화 된다. 하지만 BPR은 각 유저에 대해 보다 개인화된 랭킹을 제공하기 위해 아이템 페어(어떤 아이템을 더 선호하는지)를 포함한 최적화를 진행하게 된다.
즉 미래에 기존 방식대로 negative feedback으로 다 처리하게 되면 미래에 랭킹을 매겨야 하지만 negative가 되어버린 즉, 관측되지 않은 데이터들은 학습중에 negative feedback의 형태로 학습 알고리즘에 제공됨.
Formalization
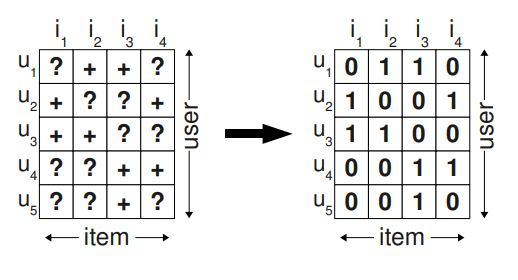
즉 기존에 ‘+’ 로 된 부분은 관측된 (positive) rating이고 ‘?’는 관측되지 않은 feedback 이다.
보통의 경우 오른쪽 처럼 0을 채워서 관측되지 않은 부분에 대해 negative feedback으로 간주한다.
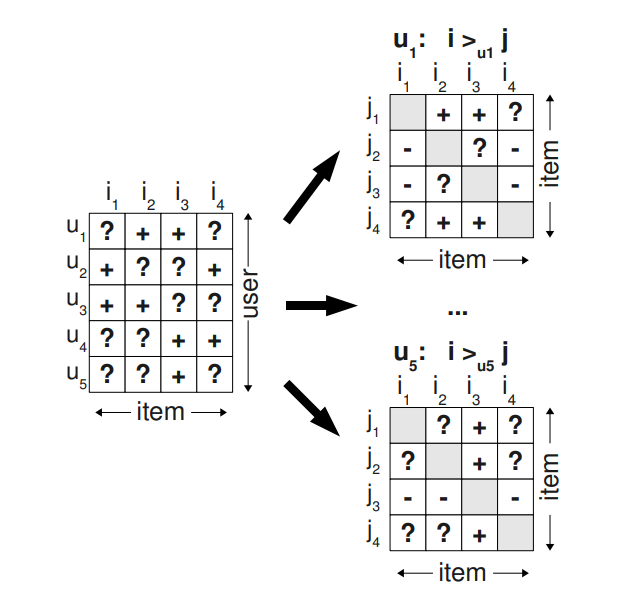
저자들이 만들고 싶은 데이터 셋의 형태는 아래와 같다.
복잡해보이는데 별거 없다. 우선 notation부터 알아보자.
$>_u$ 라는 기호가 보이는데 이 친구는 그냥 우리가 평소에 알던 대소비교 기호라고 받아들여도 좋다.
어떤 아이템 두 개가 존재해서 $I_4 >_u I_1$ 이라면 이 유저는 $I_4$를 $I_1 $ 보다 선호한다는 것이다.
이 기호에도 몇 가지 가정을 한다.(약속..?)
또한 아래와 같은 가정도 한다.
-
유저는 관측한 아이템을 ($(u,i) \in S$) 는 모든 관측되지 않은 아이템보다 선호하다.
- 관측된 피드백 (위 행렬에서 ‘+’) 끼리는 선호도 비교가 불가능하다.
- 마찬가지로 관측되지 않은 피드백 끼리도 선호도 비교가 불가능하다.
이를 공식화 해서 우리의 트레이닝 데이터를 만들면
\[D_s := \{ (u,i,j)\vert i\in I^+ \wedge j \in I \backslash I^+\}\]위처럼 트레이닝 데이터를 구성하여 논문의 접근 방식을 사용하고, 단일 아이템에 대한 점수를 매기는 대신 아이템 페어의 순위를 지정하도록 최적화 한다. 이 접근 방식이 negative feedback으로 싸잡아서 바꾸는 것 보다 (당연히) 잘 동작한다고 한다.
Bayesian Personalized Ranking
\[p(Θ\vert >_u) \propto p(>_u \vert Θ)p(Θ)\]PMF에서 봤던 그 느낌 그대로 가면 된다.
posterior 최대화 할거고, 오른쪽은 likelihood * prior 이다.
단 독립에 대한 가정을 할건데.
- 유저들은 독립이다.
- 특정 유저의 아이템에 대한 랭킹은 독립이다.
위 수식 처럼 베르누이 분포 형태로 표현 가능하다.
위에서 가정한 totality와 antisymmetry로 인해 위의 공식은 아래처럼 단순화 가능하다.
아직까지는 개인화된 전체 순서가 보장되진 않음.
아까 가정했던 세 가지 성질(totality, antisymmetry, transitivity)가 만족되야함.
이를 위해 사용자가 아이템 $j$보다 아이템 $i$를 선호하는 개별 확률을 정의함.
\[p(i>_u j \vert Θ) := \sigma(\hat x_{uij}(Θ))\]$\hat x_{uij}$는 유저 아이템 사이의 관계를 캡처하는 모델 파라미터 벡터의 실수 값 함수이다.
이 관계를 모델링하는 작업을 MF나 KNN을 통해 수행할 수 있음.
Prior는 평균이 0인 가우시안 분포를 가정함.
따라서 우리의 MAP 수식 전개는 다음과 같음.
BPR Learning Algorithm
표준 GD는 우리 태스크에서 적절한 방법이 아님.
여기서는 SGD를 개선해서 bootstrap sampling of training triples을 기반으로 하는 SGD를 사용함.
표준 GD는 ‘올바른’방향으로 하강하지만 수렴은 느리다.
| $D_s$ 에 O( | S | I | ) training triple이 있으므로 각 업데이트 단계에서 전체 기울기를 계산하는 것이 불가능하다. |
솔직히 이거 무슨 뜻인지 모르겠다… 왜 계산 불가능하지..?(구글링 해봐도 안나오는데 나중에 GD 한번 제대로 파보고 다시 돌아 와야 할듯.)
full gradient descent로 BPR-Opt를 최적화 하기 위해 사용하면 관측된 집합과 관측되지 않은 집합의 언밸런스 때문에 수렴속도가 매우 느려진다.
일반적으로 관측된 데이터 $i$가 관측되지 않은 $j$보다 당연히 많으므로, $(u, i , j_n)$ 의 형태로 $j$만 바뀌는 형태의 데이터를 연속해서 업데이트하게 되는데 이러한 경우 수렴속도가 늦어지고 결과도 좋지 않다고 함.(그래디언트가 $i$쪽에 너무 치중됨)
일반적인 SGD도 좋은 선택이지만 훈련 페어가 순회되는 순서가 중요하다고 한다.
아이템 별로, 유저 별로 데이터를 탐색하는 일반적인 접근 방식은 위에서 말한 비슷한 형태의 연속 업데이트가 존재하기 때문에 수렴성이 좋지 않다고 한다.
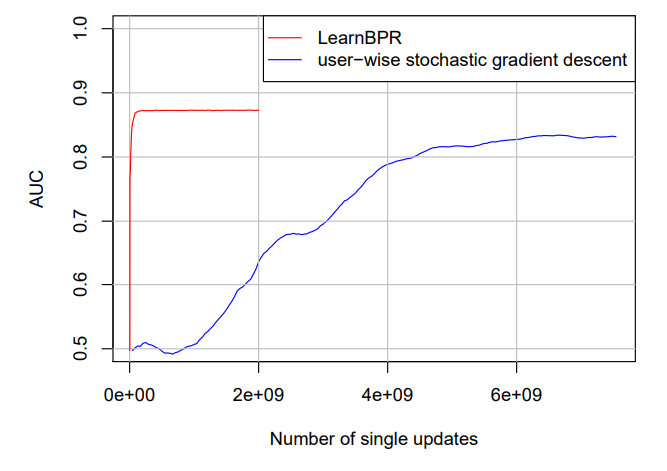
이 문제를 해결하기 위해 균등 분포로 triple을 선택하는 SGD를 사용한다.
당연히 수렴속도가 엄청 빠르고 성능도 좋아진다.
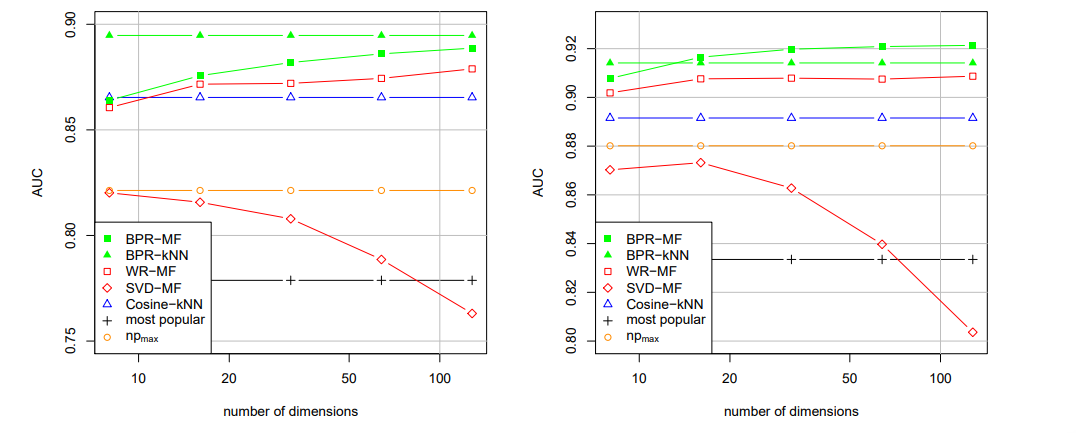
이 뒤에 내용은 기존에 제안된 알고리즘에 BPR을 어떻게 적용하는지에 대한 내용이므로 관심 있으면 논문을 참고하길 바란다.

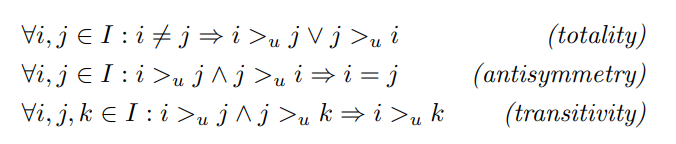
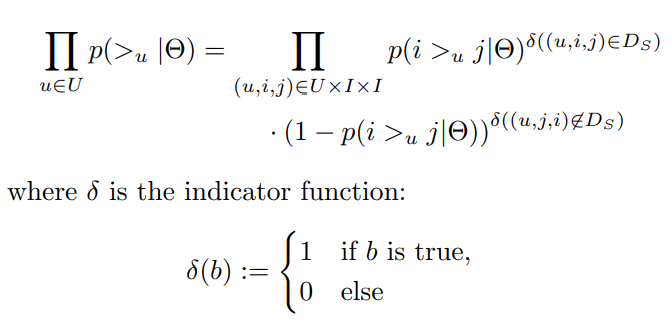
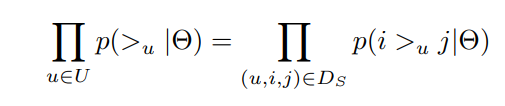
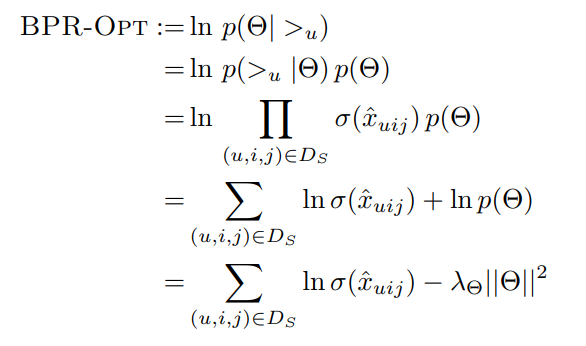
Comments