Matrix Factorization Techniques for Recommender Systems
08 Jul 2021 | Recommend논문이 나온 시점 까지의 전반적인 Matrix Factorization 테크닉을 다룸.
Contents
- Basic Matrix Factorization
- Basic Matrix Factorization + Norm based Regularization
- Two approaches to minimizing
- Basic Matrix Factorization + Norm based Regularization + Bias term
- Temporal Dynamics
- Matrix Factorization + Norm based Regularization + Implicit preference + Confidence
Basic Matrix Factorization을 통해 user, item latent matrix를 만들고, user item latent vector의 내적을 통해 레이팅을 추정한다.
\[\hat r = q_i^T p_u\tag{1}\]이러한 Factorization 과정은 컨벤션한 SVD로 수행하지만… 사실 이게 말처럼 쉽지는 않다.
기본적으로 우리가 가지고 있는 레이팅 행렬 R은 unknown값이 많은 Sparse한 행렬이라서 그냥 그대로 풀게되면 오버 피팅이 일어나기 쉽기도 하고 non-convex 문제라 풀기 어렵다.
그래서 기존의 문제 해결 방법은 unknown 값들을 채우는 것이 었는데, 이 또한 문제가 많다. 채우게 되면 dense-matrix로 바뀌어서 computational cost가 너무 높아지고, 심지어 (이상한 값으로) 잘 못 채울 가능성도 높다. 이러한 두 가지 단점을 가지고 레이팅 행렬을 채워서 사용하는 방법은 바람직 하지 못하다.
그래서 최근의 방법은 norm-based regularization을 통해 오버피팅을 막는다고 한다. 수식은 다음과 같음.
\[min\sum\limits_{(u,i)\in K} (r_{ui}-q_i^Tp_u)^2 + \lambda(\vert\vert q_i\vert\vert^2 + \vert\vert p_u\vert\vert^2)\tag{2}\]러프하게 생각하면 우리가 딥러닝에서 쓰는 것 처럼 latent vector들이 과도하게 기존의 레이팅을 맞추기 위해 high variance를 가지지 말라고 규제의 역할을 할 수도 있는 것이고, 우리가 기존의 알고있던 최적화 관점에서는 low rank approximation을 위해 non-convex한 low rank minimization 문제를 convex한 (nuclear) norm minimization으로 치환한 것으로도 생각할 수 있을 것 같다.
우리가 최적화 해야할 로스 함수는 설정했는데, 어떤 알고리즘을 통해 최적화를 진행할까?
우선 기존의 SGD를 사용하는 방법과 ALS(Alternating Least Squarse)를 사용하는 두 가지 방법이 존재한다.
SGD는 자주 나오는 개념이니 넘어가고 ALS만 살펴보자.
우리의 latent vector $q_i,\ p_u$는 알 수 없다. 따라서 우리의 로스 함수는 non-convex이다.
그런데, 하나의 latent vector를 고정하고 수식을 보게 되면 이는 quadratic 형태가 되므로 우리는 이 수식을 최적화 할 수 있게 된다.
따라서 ALS는 이름 그래도 하나를 고정하고 하나를 최적화 하는 것을 교대로 수행하게 된다.(또한 수렴성도 보장한다.)
물론 SGD가 더 쉽고 빠르지만 ALS를 사용하는 것이 좋은 두 가지 경우가 있다고 한다.
- 추천 시스템을 병렬화 해서 사용할 때
- 교대로 업데이트 하니까 병렬화된 시스템에서 더 효율적이라고 생각할 수 있다.
- implicit data 위주일 때
- 트레이닝 셋이 sparse하다고 고려할 수 없기 때문에(?) GD처럼 각 트레이닝 셋을 반복 하는 것 보다 ALS가 실용적이라고 한다.(솔직히 뭔말인지 잘 모르겠다..)
우리가 현실 세계의 문제를 다루기 때문에 기본적으로 이러한 환경에서 수집된 데이터는 bias 되어 있다.
단순한 예시로 인기도 편향을 생각해보자. 멜론 음악 차트의 경우 1위를 찍은 음악은 메인페이지의 UI에서 바로 보이게 되고 이는 더 많은 유저에게 노출이 되고 -> 자연스럽게 더욱 더 많이 플레이 될 것이다.(이러니까 사재기를 하지…)
아무튼 이러한 편향이 심하기 때문에 우리는 기존의 로스 함수를 편향을 고려해서 실제 user-item의 상호작용만 캡처할 수 있도록 모델링 해야 한다.
따라서 bias를 포함한 레이팅을 다음과 같이 표기한다.
\[b_{ui} = \mu + b_i + b_u\tag{3}\]- $\mu$ : 전체 평균
- $b_u$ : 유저의 평균으로 부터 편차(보통 유저보다 점수를 잘 주는 편인지, 짜게 주는 편인지)
- $b_i$ : 아이템의 평균으로 부터 편차(보통 아이템보다 인기가 많은지, 적은지)
예를 들어 영화의 전체 평균($\mu$)은 3.7점이다, 타이타닉 이라는 영화는 평균보다 0.5점이 높다.($b_i$), 아이유는 평균 유저들 보다 점수를 0.3점 정도 짜게 주는 편이다.($b_u$)
따라서 이를 모두 고려한 레이팅은 $(3.7 + 0.5 - 0.3) = 3.9$ 이다.
우리의 수식 (1)을 편향을 고려한 수식으로 변경해보자.
\[\hat r_{ui} = \mu + b_u + b_i + q^T_ip_u \tag{4}\]즉 우리의 추정 레이팅은 편향을 고려한 레이팅 + latent vector의 내적으로 구성된다.
따라서 이러한 편향을 고려한 로스 함수도 다시 다음과 같의 정의할 수 있다.
\[min\sum\limits_{(u,i)\in K} (r_{ui}-\mu -b_u -b_i -q_i^Tp_u)^2 + \lambda(\vert\vert q_i\vert\vert^2 + \vert\vert p_u\vert\vert^2 + b_u^2 + b_i^2)\tag{5}\]지금까진 고려하지 않았지만 추천시스템에선 시간에 변화에 따른 선호도 변화도 고려할 수 있다.
예를 들면 특정 영화가 처음 나와서 홍보를 많이 하는 경우 선호도가 올라가지만 시간이 지남에 따라 점차 떨어질 것을 알 수 있다.
또 다른 시간에 대한 관점은 특정 유저의 기준 점수가 시간에 따라 변할 수 있다는 것이다.(평점 4점을 주던 유저가 평점 3점으로 바뀌는 경우)
유저의 경우 시간에 따라 선호도가 변하지만 아이템 자체는 static 하므로 우리는 기존 식에서 $q_i$를 제외한 term에 대해 시간에 대한 함수로 바꿀 수 있다.
$q_i$ 를 시간에 대한 함수로 보지 않으면서 왜 $b_i$ 는 시간에 대한 함수로 볼까..?
아무래도 $b_i$ 와 같은 바이어스도 결국 사람에 의한 영향력 때문에 생기므로 인과관계가 있다고 보는 것 같음.
따라서 우리의 수식 (4)는 다음과 같이 변경된다.
\[\hat r_{ui} = \mu + b_u(t) + b_i(t) + q^T_ip_u(t) \tag{6}\]마지막으로 implicit data를 통해 선호도를 표현하는 많은 추천 시스템에서는 이러한 선호도를 정량화 하기가 어렵다.
따라서 ‘‘좋아 할만한 것’’ , ‘‘좋아하지 않을 것 ‘’ 의 이진 분류로 밖에 표현할 수 없고, 이러한 경우에 예상 선호도와 함께 신뢰도를 첨부하는 것이 중요하다.
따라서 신뢰도를 포함한 로스 함수를 다음과 같이 작성할 수 있다.
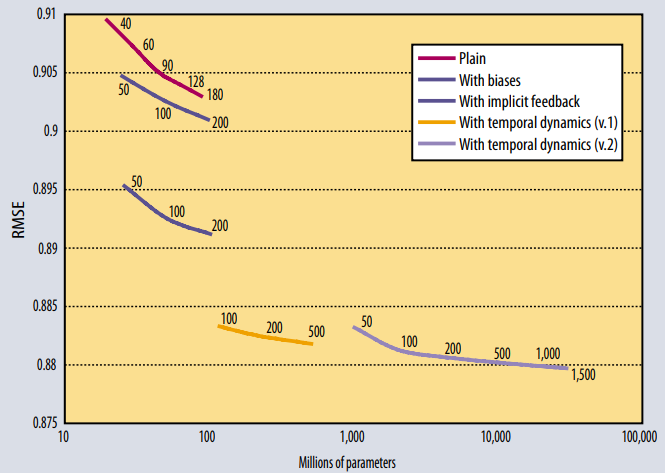
\[min\sum\limits_{(u,i)\in K} c_{ui}(r_{ui}-\mu -b_u -b_i -q_i^Tp_u)^2 + \lambda(\vert\vert q_i\vert\vert^2 + \vert\vert p_u\vert\vert^2 + b_u^2 + b_i^2)\tag{7}\]Netfilx Prize에 사용된 모델들 Figure 인데, 시간을 고려한 알고리즘이 꽤나 잘 동작하는 것을 볼 수 있음.

Comments