Item-Based Collaborative Filtering Recommendation Algorithms
04 Jul 2021 | Recommendsvd와 마찬가지로 sarwar의 논문 item-based CF에 대한 내용을 다룬다.
Summary
- User-Based
- PROS
- LSA를 사용하면 퍼포먼스의 향상이 있다.
- 추천 프로세스의 다양성이 있다.(Serendipity)
- CONS
- Sparsity
- Cold start
- Scalability
- PROS
- Item-Based
- PROS
- 전반적으로 User-based보다 퍼포먼스가 좋다.
- 아이템이 유저에 비해 static 하기 때문에 precomputationl cost가 적다(즉, scalability가 좋다.)
- CONS
- LSA를 사용하면 부정적인 영향을 미친다.
- User-Based에 비해 Serendipity가 떨어진다.
- PROS
CF기반의 추천 시스템은 두 가지 챌린지가 있는데
- Scalability
- improve the quality of the recommend system
이다. 본 논문은 item-based CF를 제안하며 이 방식이 user-based 방식 보다 계산적인 측면에서 좋고(scalability)
추천의 퀄리티도 더 좋다는 것을 실험적으로 보여준다.
item-based라고 해서 특별할 건 없다. 기존의 user-based 방식이 비슷한 유저를 먼저 찾고, 그 유저가 선호한 아이템을 추천한 방식이라면 item-based는 비슷한 아이템을 먼저 찾는 방식이다.
저자들은 여전히 유사도를 기반으로한 K-NN 모델을 사용하는데, 저자들이 주장하는 바는 다음과 같다.
user-item pair에서 item이 좀 더 static한 성질을 가지고 있으니, 미리 계산해서 사용하는 측면에서 item을 기반으로 유사도를 계산하면 scalability가 user-based에 비해 더 낫다.
또한 본 논문에서는 기존의 코사인 유사도가 레이팅 스케일이 다른 경우를 고려하지 못하기 때문에 이를 조금 수정한 Adjusted Cosine Similarity를 제안하는데 다음과 같다.
\[sim(i,j) = \frac{\sum_{u \in U} (R_{u,i} - \bar R_u)(R_{u,j}-\bar R_u)}{\sqrt{\sum\limits_{u \in U}(R_{u,i}-\bar R_u)^2 }\sqrt{\sum\limits_{u \in U}(R_{u,j}-\bar R_u)^2 }}\]Pearson Correlation과 비슷한데 그냥 유저의 평균 레이팅을 빼준 형태이다.
본 논문에서 또 새로운 방식의 계산(트릭)을 하나 사용하는데, 레이팅을 예측하기 위해 결과값을 더할 때 보통 weighted sum 형태를 사용하는데 여기서는 Regression 수식을 사용해 근사시켜서 레이팅을 더한다.
저자들은 코사인 유사도나 상관관계를 사용할 때 계산된 유사성이 두 레이팅 벡터가 유클리드 공간에서 멀리 떨어져 있을 수 있지만, 매우 높은 유사도를 가질 수 있는 경우를 고려해서 이러한 접근방식을 채택했다고 한다.
솔직히 위 의 구체적인 예시가 무엇인지는 모르겠으나 코사인 유사도 같은 경우 벡터단위의 각도만 보게 되는데, 동일한 차원의 두 레이팅 벡터가 주어져있다고 가정하고 하나는 모두 1점으로 매겨지고[1,1, …] 하나는 모두 5점으로 매겨졌다고 치면[5,5, …] 이 두 벡터는 의미적으로 봐도 유클리드 공간에서 봐도 굉장히 멀리 떨어져 있게 된다. 하지만 코사인 유사도의 경유 유닛 벡터로 바꾸고 ‘‘각도’’ 만 보기 때문에 두 벡터는 한 벡터의 스칼라 배로 표현 가능하므로 5*[1,1, …] = [5,5, …] 둘 사이의 각도는 0이 되어 유사도가 1이 되버리는 상황을 말하는게 아닐까 싶다.
이 저자는 CF의 limitation에서도 scalability를 참 좋아하는 것 같다.
이를 위해 comuptational 성능과 big O 표기법을 참 좋아하는데 이 논문에서도 들어난다.
앞서 말한 item이 static한 성질을 지니고 있으니 유사도를 precomputing해서 만들어 놓고 쿼리를 보내서 필요할 때 마다 조회하는 식으로 사용하면 시간을 절약할 수 있다고 한다.
n개의 아이템이 존재할 때 소요되는 시간은 $O(n^2)$이라고 한다.
Experiments
실험은 하이퍼 파라미터를 바꿔가면서 user-based 기반과 item-based(논문 제안 방식)을 비교한다.
적절한 하이퍼 파라미터를 찾으려고 노력하는데, 여기서 사용되는 하이퍼 파라미터는 model size(K-nn), train/test ration 등이 존재한다.
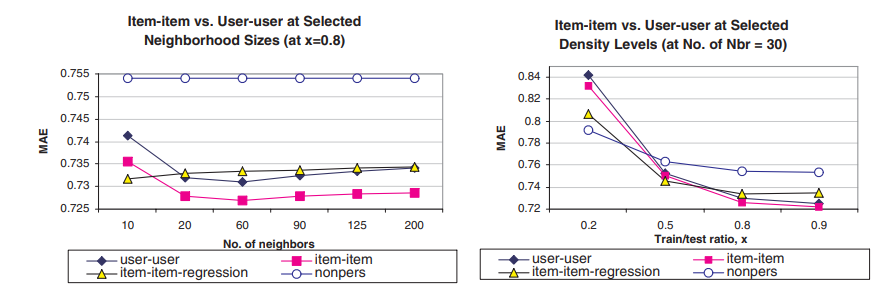
앞선 저자들이 제안한 Adjust Cosine이 실험에서 MAE가 가장 낮게 나와 성능이 좋다는 것을 실험적으로 보여주고 있고, 또한 regression based 알고리즘이 잘 동작한다는 것도 실험 적으로 보여준다.

Comments