How Does Batch Normalization Help Optimization?

Abstract

BN은 빠르고 안정적으로 DNN을 학습시킬 수 있게 해줍니다. 그러나 BN의 인기에도 불구하고, 왜 잘 동작하는지에 대한 이유는 아직 잘 알려져 있지 않습니다.

대부분은 기존 논문에 언급한대로, ‘internal covariate shift’를 줄이기 위해 훈련중에 레이어의 입력 분포를 제어하는 데서 비롯된다라고 믿습니다.

논문에서는 레이어의 입력에 대한 분산을 컨트롤 하는 것이 BN의 성공과 거의 관련이 없음을 보여줍니다.

대신, 훈련 과정에 대한 BN의 더 근본적인 영향을 발견합니다 최적화 환경(landscape)을 훨씬 더 매끄럽게 만듭니다.

이러한 변화는 그래디언트를 예측 가능하고 더 안정적으로 동작하도록 유도하여 더 빠른 훈련을 가능케합니다.

Introduction

BN은 레이어의 입력 분포를 안정화하여 신경망 훈련을 개선하는 것을 목표로 하는 기술입니다.

이러한 분포의 처음 두 모멘트(mean, var)를 제어하는 추가 네트워크 층을 도입해서 사용합니다.

BN이 ISC를 해결함으로써 퍼포먼스의 향상을 이뤄냈다고 널리 받아들여지고 있지만, 이를 뒷받침하는 구체적인 증거가 딱히 존재하지 않습니다. 여전히 ISC와 트레이닝 퍼포먼스 사이의 연관성을 이해하지 못합니다.

시작점은 성능 향상과 ISC 이동의 감소 사이에 어떤 연관성이 없다는 것을 증명하는 것입니다. 사실 어떤 의미에서 BN은 ISC를 줄이지 않을 수도 있습니다.

그런 다음 BN 성공의 근본 원인을 파악하는데 집중합니다.

특히 BN이 기본적인 방식으로 네트워크 교육에 영향을 미친다는 것을 보여줍니다. 이는 해당 최적화 문제의 환경을 훨씬 더 매끄럽게 만듭니다.(앞서 언급) 이러한 smooth는 그래디언트를 예측 가능하고 더 안정적으로 동작하도록 유도하여 더 빠른 훈련을 가능케합니다.

우리는 이러한 발견과 이론적 정당성에 대한 경험적 증명을 제공합니다.

우리는 기본 조건에서 손실과 그래디언트($\beta-smoothness$ 라고도 불리는 )모두 Lipschitzness가 BN을 사용하는 모델에서 향상된다는 것을 증명합니다.

(We prove that, under natural conditions, the Lipschitzness of both the loss and the gradients (also known as β-smoothness [21]) are improved in models with BatchNorm)

• natural condition ?
• Lipschitzness?
• $\beta-smoothness$?

마지막으로, 이 smooth의 효과는 BN과 고유하게 연결되지 않습니다.

다른 많은 자연 정규화 기술은 유사한(때로는 더 강력한)효과를 가지고 있습니다. 특히 그들은 모두 트레이닝 퍼포먼스에서 유사한 개선을 제공합니다.

우리는 BN과 같은 기본 기술의 뿌리를 이해하면 신경망 훈련의 근본적인 복잡성을 훨씬 더 잘 이해할 수 있고 이 맥락에서 알고리즘 발전을 더 많이 알릴 수 있을 것이라고 믿습니다.

Batch normalization and internal covariate shift

일반적으로 BN은 훈련중에 레이어에 대한 입력 분포(미니 배치를 통해)를 안정화 하는 것을 목표로 하는 메커니즘입니다.

앞서 말했듯, BN의 주요 개발 동기중 하나는 ICS의 감소였고, 이런 변화가 훈련과정에 해로운 영향을 미치는 것으로 여겨졌습니다.

이전 레이어의 파라미터 업데이트로 인한 네트워크 레이어의 입력 분포가 변경되는 현상

논문에서는 ISC와 BN간의 연관성을 조사합니다. 특히, BN을 사용하거나 사용하지 않고 CIFAR-10에서 표준 VGG 아키텍처를 학습합니다.

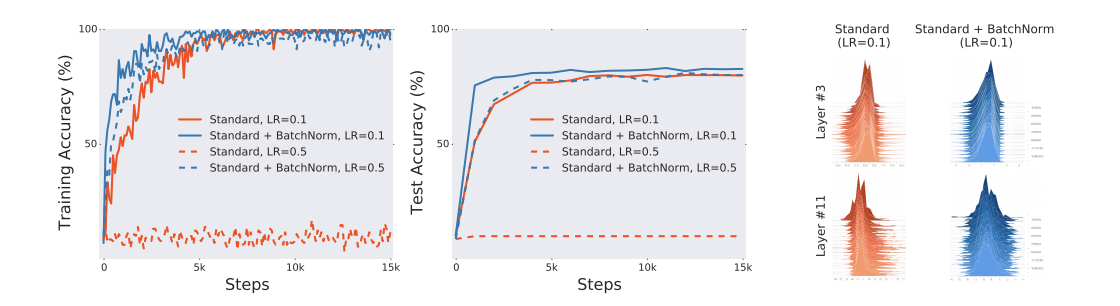
당연하게도 BN을 사용한 모델의 퍼포먼스가 크게 향상되었음을 볼 수 있습니다.

위 그림의 오른쪽 패널은 임의의 입력 분포(배치에 대한)를 플로팅 하여 레이어 입력 분포를 시각화 한 것 입니다. 보면 알겠지만 분포의 안정성에 대해서는 별 차이가 없는 것 같습니다. 위를 통해 두 가지 의문점이 발생합니다.

• BN이 ISC와 관련이 있는 것이 맞는가?
• BN의 레이어 입력 분포의 안정화는 ICS를 줄이는 데도 효과적인가?

Does BatchNorm’s performance stem from controlling internal covariate shift?

기존의 핵심 주장(ICS의 감소)은 레이어 입력 분포의 평균과 분산을 제어하는 것이 훈련 성능 향상과 직접적으로 연결되어 있다는 것입니다. 그러나 이 주장을 입증할 수 있을까요?

BN 레이어 뒤에 무작위 노이즈가 추가된 네트워크를 훈련시키는 실험을 해봅시다. 이러한 노이즈의 주입은 모든 스텝에서 활성화를 왜곡하는 심각한 ICS를 유발합니다. 결과적으로 레이어의 모든 유닛은 각 타입 스텝에서 다른 입력 분포를 경험합니다.

이후 의도적으로 주입한 불안정성이 BN의 성능에 미치는 영향을 측정합니다. 아래 그림은 표준 아킽텍처, BN 및 ‘노이즈가 있는’ BN의 트레이닝을 시각화 합니다.

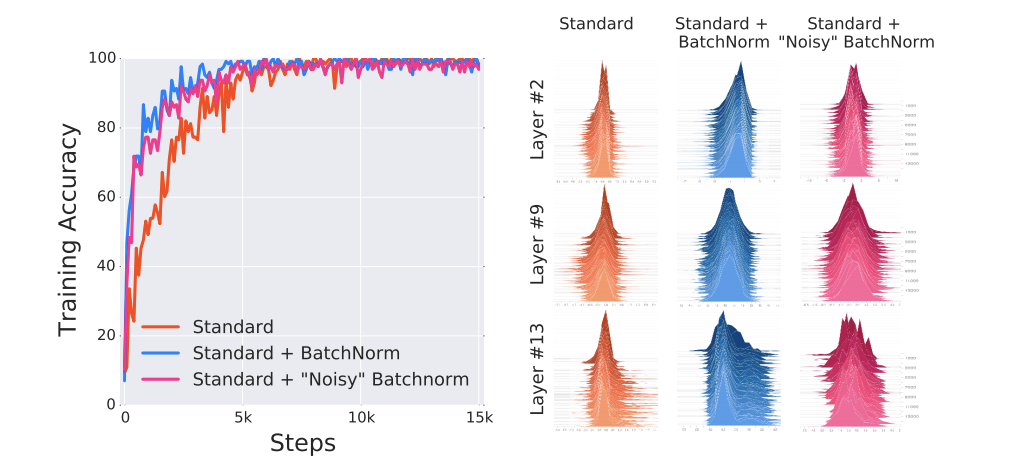
결론은 BN레이어의 모델과 ‘노이즈를 포함한’ BN 레이어를 포함한 모델 간의 성능은 거의 존재하지 않으며 둘 다 표준 네트워크에 비해 성능이 훨씬 뛰어납니다. 비록 ‘노이즈를 포함한’ BN 네트워크가 덜 안정적인 분포를 가질지라도 훈련 측면에서 더 나은 성능을 보입니다.

이러한 결과는 BN으로 인한 성능 향상이 레이어 입력 분포의 안정성 증가에서 비롯된다는 주장과 일치하기 어렵습니다.

Is BatchNorm reducing internal covariate shift?

앞선 섹션에서 ICS가 훈련 성능과 직접적으로 연결되지 않음을 보았습니다. 그러나 여전히 궁금한 점은 훈련 성능에 직접적으로 미치는 어떤 효과가 BN으로 인해서 발생한다는 점입니다. ‘어떤 효과’ 가 BN으로 인해서 모델의 훈련 성능을 향상시킬까요?

각 레이어는 입력이 주어지면 일부 손실 함수를 최적화 하는 경험적 위험 최소화 문제(empirical risk minimization)를 해결하는 것으로 볼 수 있습니다.(뒤의 레이어를 포함할 수 있음)

Empirical risk는 딥러닝에서 Cost라고 생각하면 됩니다.

training set에서 Loss의 평균을 구해 risk를 근사한 것. risk를 최소화하는 대신 empirical risk를 최소화하는 $\hat f$를 찾는 것

risk는 $R(f)=E[L(f(x),y)]$ 즉 ,loss function의 기댓값으로 정의할 수 있는데, 확률 변수 $X,Y$를 표현하기 위한 결합확률분포함수가 필요한데 $P(X,Y)$를 알 수 없으므로 근사해서 문제를 푸는 것.

출처: JIMIN

이전 레이어의 파라미터를 업데이트하면 이러한 입력이 변경되므로 경험적 위험 최소화 문제 자체가 변경됩니다. 이런 현상이 기존의 ICS의 감소를 통해 BN의 성능 향상을 주장하는 직관의 핵심입니다.(그러나 이게 아닌 것임을 이전 섹션에서 밝혔습니다.)

이 질문에 대답하기 위해 기본 최적화 작업과 더 밀접한 ICS에 대한 더 넓은 개념을 고려합니다.(결국 BN 성공의 대부분은 최적화 특성입니다.)

훈련 절차는 first-order method이므로 loss의 그래디언트에 관심을 가져 봅시다. 이전 레이어의 파라미터 업데이트에 대한 반응으로 레이어의 파라미터가 ‘조정’되어야 하는 정도를 정량화 하기 위해 모든 이전 레이어에 대한 업데이트 전후의 레이어 그래디언트간의 차이를 측정합니다.

Deifinition 2.1

$\mathcal L$을 loss, $W_1^{(t)},…,W_k^{(t)}$를 각 레이어의 파라미터, $(x^{(t)},y^{(t)})$를 시간 $t$에서 네트워크를 훈련시키는 데 사용되는 인풋-레이블 쌍의 배치라고 합시다.

시간 $t$에서 활성화 $i$의 ICS를 $\vert\vert G_{t,i}-G’_{t,i}\vert\vert_2$의 차이로 정의합니다.

$G_{t,i}$는 모든 레이어를 동시에 업데이트하는 동안 적용될 레이어 파라미터의 기울기에 해당합니다.(즉, 시점 $t$에서 $i$번째 레이어의 그래디언트이며, $W_i^{(t)}$에 대한 loss function의 derivative )

반면에 $G’_{t,i}$는 모든 이전 레이어가 새 값으로 업데이트 된 후 동일한 그래디언트입니다.

따라서 $G,G’$의 차이는 입력의 변경으로 인한 $W_i$의 최적화 환경의 변화를 반영합니다. 따라서 훈련에 문제가 될 수 있는 레이어 간 종속성의 효과를 정확하게 포착합니다.

위 정의를 사용하여 BN레이어가 있거나 없는 ICS의 범위를 측정합니다. BN에 대한 기존의 이해는 네트워크에 BN을 추가하면 $G$와 $G’$의 상관 관계가 증가하여 ICS를 줄여야 함을 시사합니다. 놀랍게 BN을 사용하는 네트워큰느 종종 ICS의 증가를 나타냅니다 이것은 특히 DLN(deep linear network)의 경우 두드러집니다.

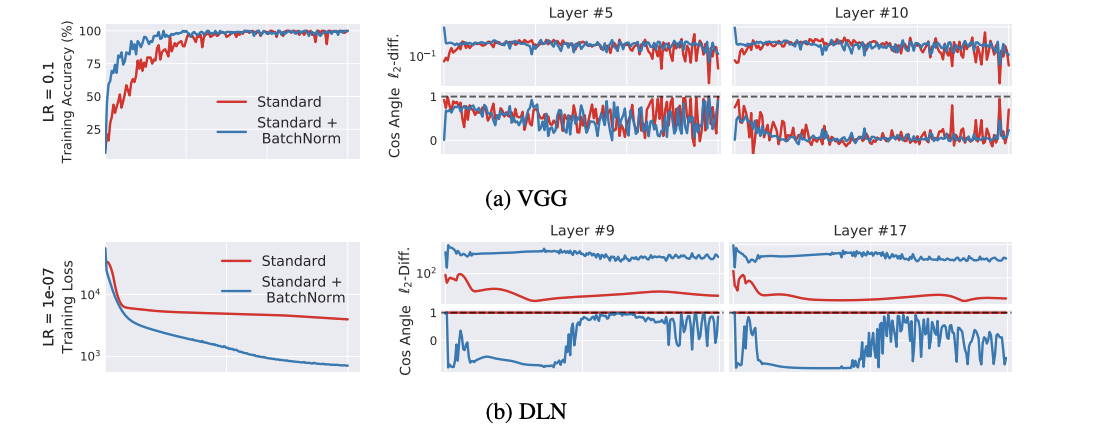
실제로 이 경우 표준 네트워크는 학습시 ICS를 거의 경험하지 않는 반면 BN의 경우 $G$와 $G’$은 거의 상관관계가 없는 것으로 보입니다.

우리는 BN네트워크가 달성된 정확도와 손실 측면에서 계속해서 훨씬 더 나은 성능을 발휘하더라도 ICS의 감소와는 관련이 없다는 것을 강조합니다.(최적화의 관점에서)

Why does BatchNorm work?

지금까지 우리의 조사는 ICS와 최적화 성능 사이에 연결이 미약하다는 것을 보여주었습니다. 그러나 BN은 학습 프로세스를 크게 개선합니다. 왜 이런지 설명 할 수 있을까요? BN의 모든 속성은 학습 과정에 분명히 도움이 됩니다. 그러나 이는 BN 메커니즘의 단순한 결과일 뿐이며 BN의 성공을 담당하는 기본 요소를 밝히는데 거의 도움이 되지 않습니다. 좀 더 근본적으로 파헤쳐 봅시다.

The smoothing effect of BatchNorm

실제로 BN이 학습 프로세스에 미치는 주요 영향에 대해 살펴봅시다. 기본적으로 BN은 최적화 문제를 reparametrizes하여 최적화 환경을 훨씬 더 매끄럽게 만듭니다.

이로 인해 발생하는 첫 번째 효과는 손실 함수의 Lipschitzness를 개선합니다. 즉, 로스가 더 작은 비율로 변하고 기울기의 크기가 제한됩니다.

BN의 reparametrization은 로스의 그래디언트를 더 많이 립시츠로 만듭니다. 즉, 로스는 훨씬 더 나은 $\beta-smoothness$를 나타냅니다.

$\vert\vert f(y)-f(x)\vert\vert \leq L\vert\vert y-x\vert\vert \quad \forall x,y\in R^n$

$\vert\vert \nabla f(y)-\nabla f(x)\vert\vert \leq \beta\vert\vert y-x\vert\vert \quad \forall x,y\in R^n$

continuously diffrentiable function $f$ 는 $\nabla f$가 $\beta-Lipschitz$일 때 $\beta-smooth$

이러한 매끄럽게 만드는 효과는 학습 알고리즘의 성능에 큰 영향을 미칩니다. 이를 이해하기 위해 바닐라 네트워크(non-BN)에서 손실 함수는 non-convex, kinks, flat regions, sharp minima를 갖는 경향이 있음을 생각해봅시다.

여기서 나오는 레퍼런스 논문 재밌어 보임

Visualizing the Loss Landscape of Neural Nets

이로 인해 GD기반 알고리즘이 불안정해집니다.(e.g. gradient exploding or vanishing 등의 이유로 학습률 및 초기화에 매우 민감함)

이제 BN의 reparametrization의 주요 의미는 그래디언트를 안정적이고 예측 가능하게 만드는 것으로 생각할 수 있습니다.

결국 그래디언트의 향상된 립시츠속성은 계산된 그래디언트 방향으로 더 큰 스텝을 수행할 때 그 방향이 정확한 추정치로 유지된다는 확신을 줍니다.

따라서 모든 그래디언트 기반 학습 알고리즘이 flat regions(gradient vanishing) or sharp local minimum(gradient exploding)과 같은 loss landscape의 갑작스러운 변화에 부딪힐 위험 없이 더 큰 스텝을 수행할 수 있습니다.

이게 BN이 LR에 둔감하다는 이유인듯.

또한 하이퍼 파라미터 선택에 덜 민감하도록 만들고 학습을 훨씬 빠르게 함.

Exploration of the optimization landscape

손실 자체의 안정성 즉, 립시츠속성으로 인한 BN의 영향을 보여주기 위해 학습 프로세스의 각 단계에 대해 로스의 그래디언트를 계산하고 해당 방향으로 이동할 때 로스가 어떻게 변하는지 측정합니다.

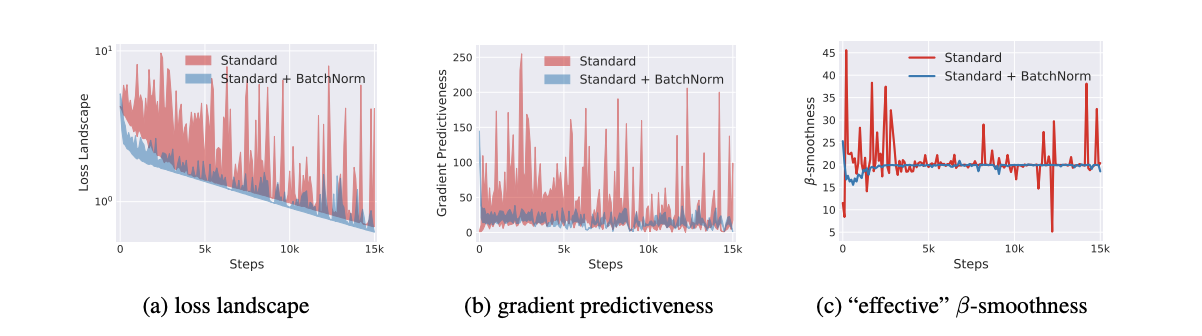
왼쪽 패널을 보면 BN을 사용중인 네트워크에 비해 바닐라 네트워크는 훈련의 초기 단계에서 그래디언트 방향을 따라 매우 광범위한 값을 가집니다.

기울기의 안정성과 예측성 증가를 설명하기 위해 학습의 주어진 포인트에서 로스의 그래디언트와 기존의 그래디언트 방향을 따라 다른 점에 해당하는 그래디언트 사이의 $l2$ 거리에 대해 측정합니다.

말이 좀 복잡한데

• (a) : loss gradient 측정
• (b) : gradient의 예측성
• (c) : gradient 방향으로 이동했을 때의 변화량

중앙 패널은 훈련 초기에 바닐라 네트워크와 BN네트워크 간의 기울기 예측이 상당한 차이를 가지는 것을 보여줍니다.

로스 그래디언트의 안정성과 립시츠속성에 대한 BN의 효과를 추가로 입증하기 위해 오른쪽 패널에 학습 전반에 걸친 바닐라 및 BN네트워크의 “effective” $\beta-smoothness$를 플로팅했습니다.(여기서 ‘effective’는 그래디언트 방향으로 이동할 때 그래디언트의 변화를 측정하는 것을 의미함.)

Is BatchNorm the best(only?) way to smoothen the landscape?

BN에 대한 우리가 새로 얻은 이해와 그 효과를 감안할 때 이 smooth 효과는 BN의 고유한 기능일까요? 아니면 다른 정규화 체계를 사용하여 유사한 효과를 얻을 수 있을까요?

몇 가지 자연 데이터 통계 기반 정규화 전략에 대해 알아봅시다.

BN처럼 활성화의 first-order moment를 수정한 다음 $p=1,2,…,\infty$에 대해 $l_p-norm$(평균 이동 전)의 평균으로 정규화 하는 방식을 연구합니다. 이런 정규화 체계의 경우 레이어의 입력 분포가 더 이상 가우스와 유사하지 않습니다. 따라서 이러한 $l_p-norm$을 사용한 정규화는 더 이상 분포 모멘트나 분포 안정성에 대한 제어를 보장하지 않습니다.(바로 아래 그림 참조)

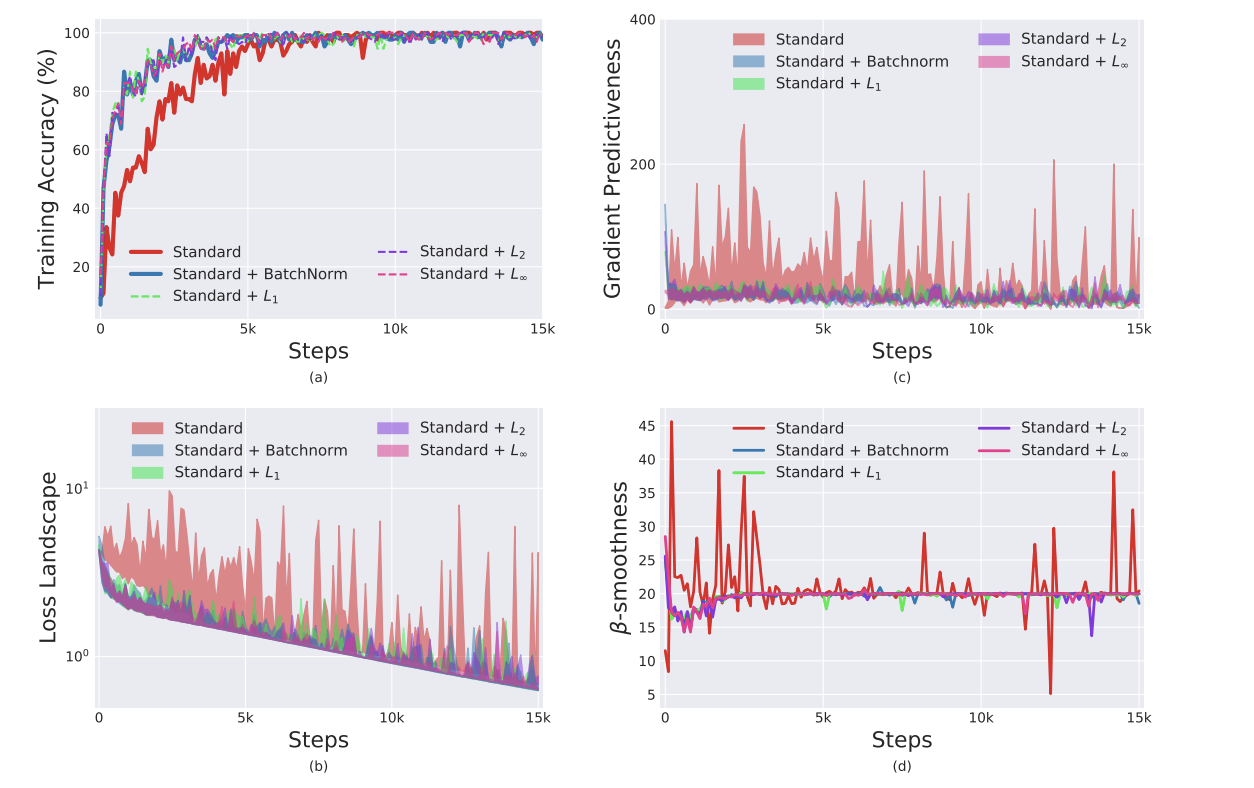
다양한 $l_p$normalization으로 훈련된 VGG 네트워크의 평가.

fig. b,c,d는 다양한 모델에서 최적화 환경의 smoothness를 나타냄.

보면 알겠지만 BN과 $l_p$는 별 차이 없다.

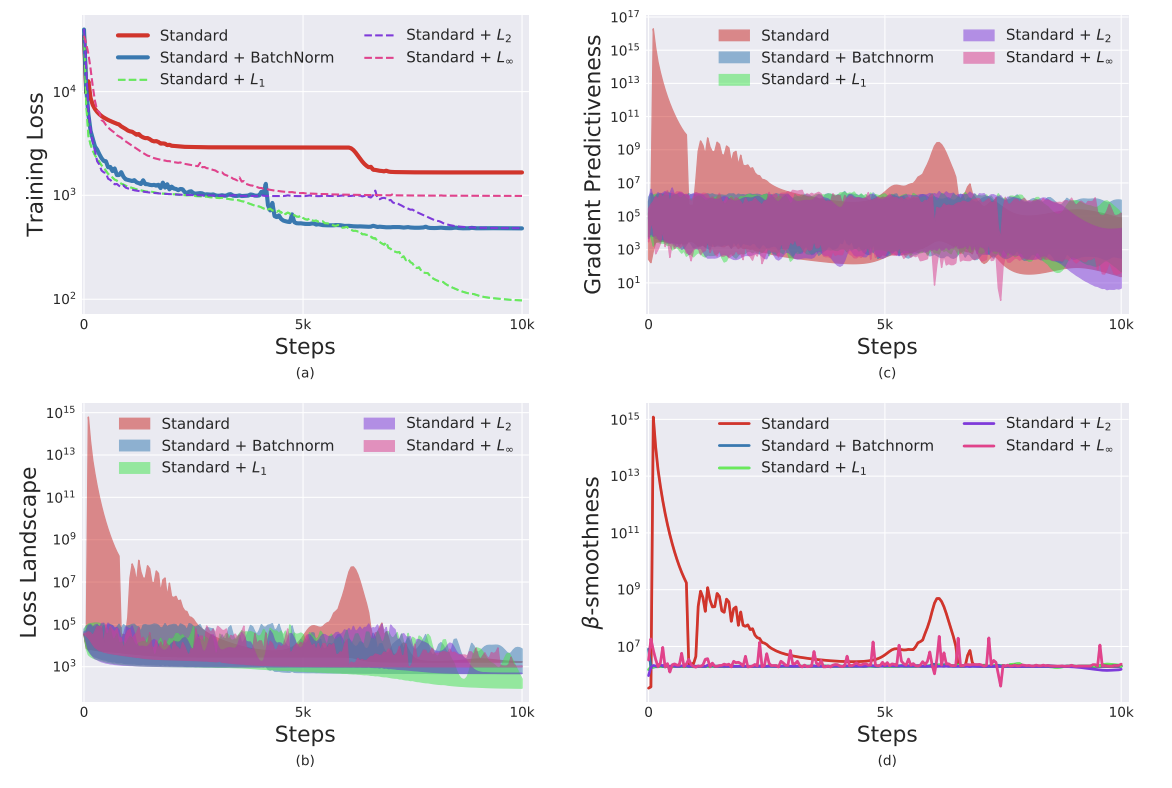
디테일은 위 그림과 같고 VGG가 아닌 DLN에 대한 평가.

$L_1$의 효과가 좋은 것을 볼 수 있다.

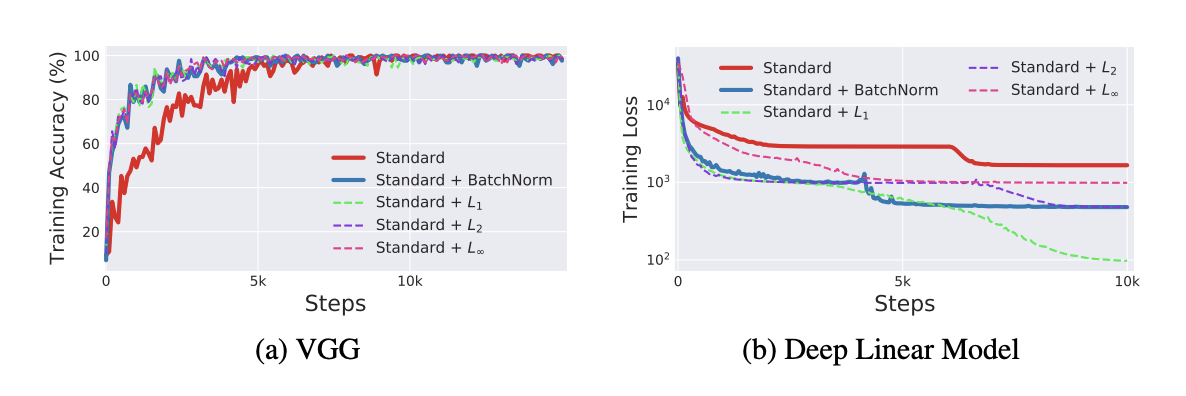
VGG와 DLN 모두에서 $l_p$가 BN 만큼 좋거나 더 우수하다는 것을 볼 수 있음.

이는 위에서 말한 것 처럼 분포 안정성(평균과 분산을 통제하는 것)이 BN을 통한 모델의 성능 향상으 주요 원인이 아닌 것을 나타냄.(그러니까 ICS 감소시켜서 잘되는 거 아니라고!)

모든 정규화 전략이 BN에 필적하는 성능을 제공하는 것으로 관찰됩니다. 사실 DLN의 경우 $l_1-norm$은 BN보다 훨씬 더 잘 수행됩니다.

또한 이런 모든 기술은 BN의 효과와 유사한 landscape의 smooth를 향상시킵니다. 이는 BN이 학습에 미치는 영향이 다소 긍정적일 수 있음을 보여줍니다. 따라서 더 나은 성능으로 이어질 수 있으므로 정규화 계획의 design space에 대한 원칙적인 탐색을 수행하는 것이 유용할 수 있습니다.

Theoretical Analysis

학습 중 주어진 단계에서 임의의 완전연결층 W 뒤에 단일 BN레이어를 추가할 때의 영향을 분석해봅시다.

분석은 단순히 입력 $x$를 정규화 하는 것이 아니라 landscape의 reparametrization에서 비롯된 효과를 포착합니다.

활성화 $y_j$에 대한 최적화 환경을 고려해봅시다. BN으로 인해 이러한 환경이 보다 잘 작동하여 립시츠 연속성 및 기울기 예측 가능 등 안정된 학습에 유리한 속성들이 존재합니다. 그런 다음 활성화 공간 환경의 이러한 개선이 가중치 공간 환경에서 최악의 경우 bounds로 변환된다는 것을 보여줍니다.

먼저 로스의 Lipschitzness를 포착하는 그래디언트의 크기 $\vert\vert\nabla_{y_i}\mathcal L\vert\vert$에 집중해봅시다.

로스의 립시츠 상수는 최적화에 중요한 역할을 합니다. 사용되는 특정 가중치 또는 로스에 대한 어떠한 가정도 없이 배치 정규화를 거친 landscape가 더 나은 립시츠 상수를 가지는 것을 보여줍니다.

또한 립시츠 상수는 활성화 $\hat y_j$가 그래디언트 $\nabla_{\hat y_j}\hat{\mathcal L}$와 상관 관계가 존재하거나 그래디언트의 평균이 0에서 벗어날 때 마다 크게 감소합니다. 이 감소는 가산적이며 BN의 스케일링이 기존 레이어의 스케일링과 동일한 경우에도 효과가 있습니다.($\sigma_j=\gamma$)

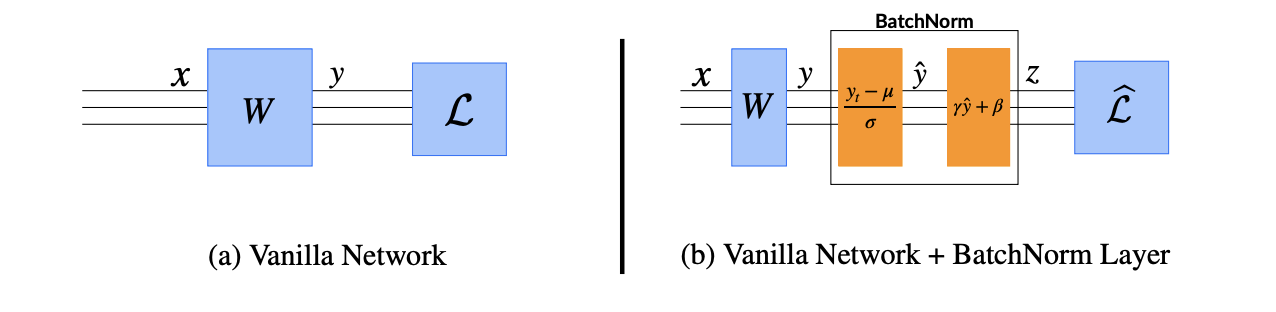
Theorem 4.1

왼쪽 텀은 BN을 적용한 그래디언트이다.

$\vert\vert\nabla_{y_i}\mathcal L\vert\vert$ 는 기존의 그래디언트인데, 두 가지 텀이 빠지는 것으로 인해 리덕션이 일어나고, $\frac{\gamma^2}{\sigma^2}$로 인해 스케일링이 발생함 여기서 $\frac{\gamma^2}{\sigma^2}$가 립시츠 상수 $L$의 역할을 한다!

자세한 증명은 Appendix를 참고하면 좋다 ㅎ..수식 주의

중간항인 $<1,\partial L/\partial y>^2$은 차원에 quadratically 비례하고, 변수에 대한 그래디언트가 변수 자체와 거의 상관 관계가 없기 때문에 마지막 항은 0에서 멀어질 것으로 예상됩니다. 추가적인 감소 외에도, $\sigma^2$은 일반적으로 큰 값을 가집니다.(Appendix Fig.8)

이제 landscape의 두 번째 속성에 집중해봅시다. BN 레이어가 추가되면 그래디언트 방향에 대한 손실 헤시안의 quadratic 형태가 입력 분산(미니 배치 분산에 대한 복원력 유도)에 의해 재조정 되고 추가 요소에 의해 감소됨을 보여줍니다.(smoothness 증가)

이 텀은 현재 포인트 주위의 그래디언트에 대한 테일러 확장의 2차 항을 캡처합니다. 따라서 이 항을 줄이면 1차 항(그래디언트)이 더 예측 가능해짐을 의미합니다.

Theorem 4.2

$Let\ \hat g_j = \nabla_{y_j}\mathcal L \ and\ H_{jj} = \frac{\partial\mathcal L}{\partial y_j\partial y_j}$

헤시안 및 내적을 포함하는 2차식 형태가 음이 아닌 경우(마일드한 가정) 위 정리는 더 많은 기울기의 예측을 의미합니다.

헤시안은 로스가 locally conex 이거나 최종 레이어에서 conex loss인 경우 positive-semi-definite 입니다.(softmax, ce, etc.. 대부분의 로스함수)

조건 $\langle\hat y_j,\hat g_j\rangle>0$은 음의 그래디언트 $\hat g_j$가 로스의 최소값을 향하는 한 유지됩니다.(정규화된 활성화.)

전반적으로 이 두가지 조건이 유지되는 한 BN 네트워크에서 수행한 스텝은 표준 네트워크 스텝 보다 더 예측 가능합니다.

로스의 헤시안이 바운딩이 되는 것으로 증명함.

러프하게 말하면 모든 헤시안의 엔트리가 BN적용 후에 더 작아지므로 smooth한 효과가 있다고 할 수 있음

아무튼 바운딩 되면 스텝을 좀 더 크게 줄 수 있음(그래디언트의 예측 가능성 증가, 즉 이 방향으로 가도 된다는 신뢰도 증가..?)