Lipschitz & Spectral norm
15 Oct 2020 | techSummary
- 함수가 립시츠 연속이면 학습을 안정적으로 할 수 있다.
- Spectral norm은 가장 큰 특이값이다.
- 선형 함수의 가장 큰 특이값은 L2norm이다.
- 가장 큰 특이값은 그래디언트와 비슷한(추상적으로) 의미를 가진다.
Definition of Lipschitz continuity
사실 개념 자체는 어렵지 않다. 그리고 꽤나 직관적이다.
어떤 함수가 다음 식을 만족하면 $K-Lipshitz\ continuous$라고 한다.
\[\vert\vert f(x)-f(y)\vert\vert\leq K\vert\vert x-y\vert\vert\]여기서 K의 최소값에 우리는 관심이 있다. 그러니까 식을 좀 변형해서 다음과 같이 쓰면,
\[\frac{\vert\vert f(x)-f(y)\vert\vert}{\vert\vert x-y\vert\vert}\leq K\]이고 이는 기울기가 $K$이하인 함수로 아주 직관적으로 생각할 수 있다.
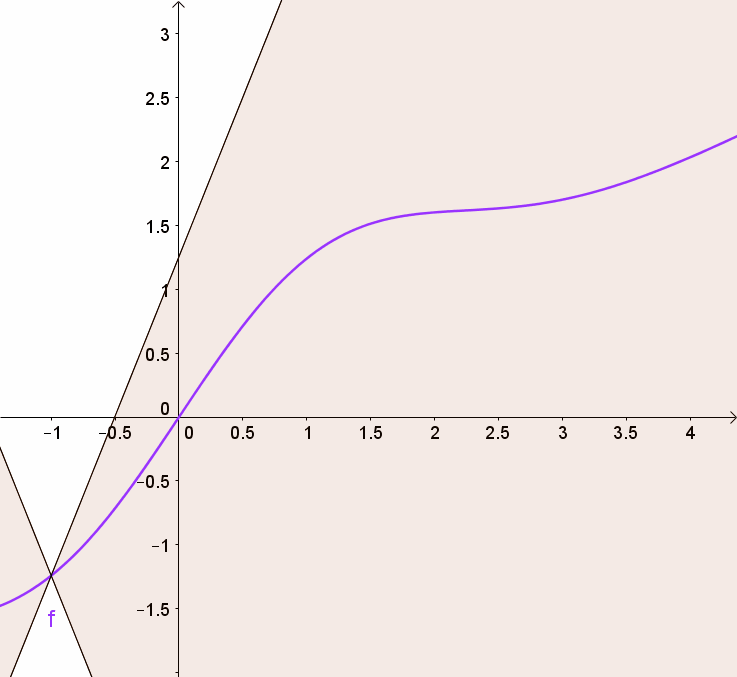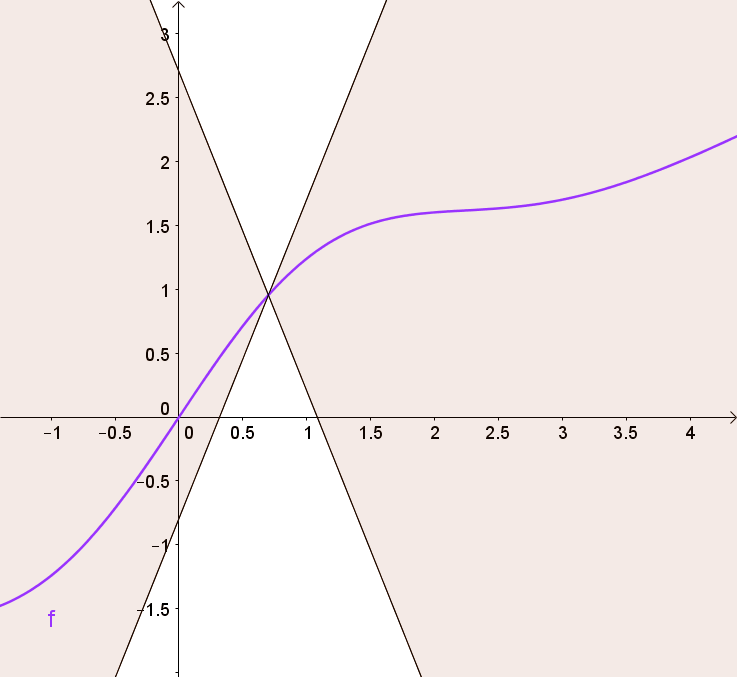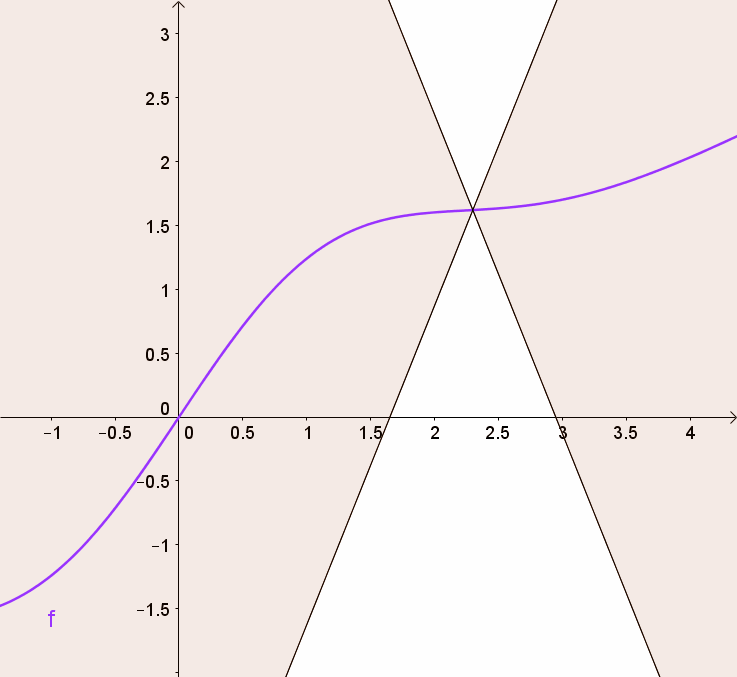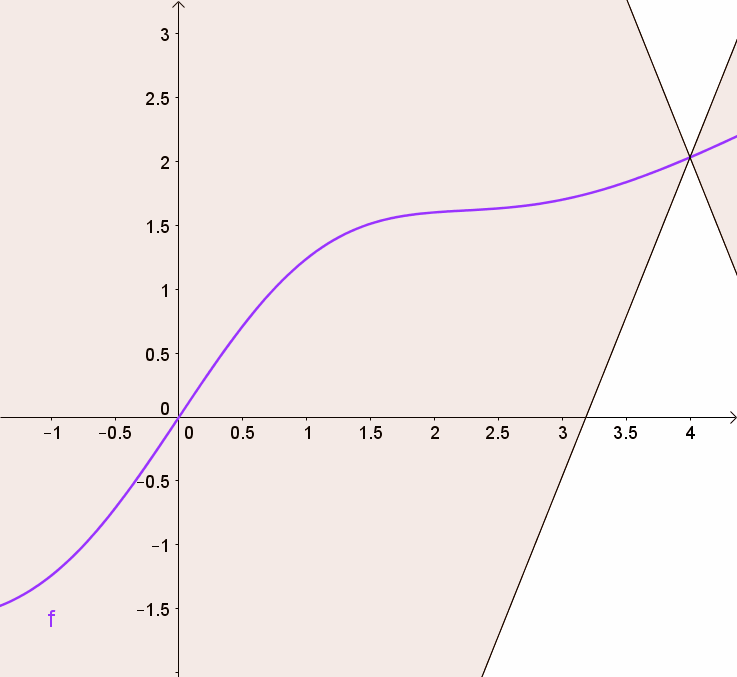
$f$의 기울기가 색칠된 영역 안에 존재함을 볼 수 있다!
이게 왜 좋은 특성이냐면 함수의 기울기가 제한된다는 말 자체가 급격하게 변하는 지점이 별로 없다, 즉 smooth해진다는 의미이다. Loss function이 smooth해지면..? 직관적으로 생각해도 학습을 안정적으로 할 수 있지 않을까?
조금 더 우리에게 친숙한 예시를 들어보자면,
Sin(x)와 Relu는 대표적인 1-Lipschitz continuous이다.
반대로 $x^2$의 경우 립시츠 연속이 아니다.
여기서 흥미로운 사실은 함수가 미분 가능할 경우 립시츠 상수는 도함수의 최댓값이라는 점!
cos(x)의 최댓값, Relu의 최댓값이 1이고 $x^2$의 최댓값은 $2x$이니까 bounded가 아님.
Multidimensional case
$R^n\rightarrow R^n$
위 함수의 spectral norm을 계산할 수 있다.
Spectral norm은 위 행렬 A의 가장 큰 singular value이다.
혹은 $A^TA(or\ AA^T)$의 가장 큰 고유값의 제곱근이다.
위를 통해 $A^TA,\ AA^T$의 고유값들은 모두 0이상이며 0이아닌 고유값들은 서로 동일하다.
$proof$
- $A^TAv=\lambda v$ $\rightarrow$ $v^TA^TAv = \lambda v^Tv$ $\rightarrow$ $(Av)^TAv = \lambda v^Tv$ $\rightarrow$ $\vert\vert Av\vert\vert^2=\lambda \vert\vert v\vert\vert^2$ 이므로 $\lambda \geq0$
- $A^TAv=\lambda v$ $\rightarrow$ $AA^T(Av) = \lambda (Av)$ 이므로 $(Av\neq0)$이면 $\lambda$는 $AA^T$의 고유값이 된다!
위와 같이 $AA^T,\ A^TA$의 공통 고유값($\sigma_1^2\geq…\geq\sigma_s^2\geq0 $)을 구하고 이들의 square root를 취한 것이 $A$의 특이값이다!
$A$는 선형이므로 $A$가 0에서 K-립시츠이면 모든 곳에서 K-립시츠이다.
\[\vert\vert Ax\vert\vert \leq K\vert\vert x\vert\vert\]따라서 모든 $x$에 대하여 다음을 만족한다.
\[<Ax,Ax>\leq K^2<x,x>\]그리고 이렇게 변형할 수 있다. (i.e. $x=\sum_ix_iv_i$)
\(<(A^TA-K^2)x,x>\leq 0\) (위식을 다 전개했다가 다시 이렇게 묶을 수 있음)
$A^TA$의 고유벡터는 orthonormal이므로,
\[<(A^TA-K^2)x,x>\\ = <(A^TA-K^2)\sum\limits_ix_iv_i,\sum\limits_jx_jv_j> \\ = \sum\limits_i\sum\limits_jx_ix_j<(A^TA-K^2)v_i,v_j>\\ =\sum\limits_i(\lambda_i-K^2)x_i^2 \leq 0 \Rightarrow \sum\limits_i(K^2-\lambda_i)x_i^2\geq0\]$A^TA$는 positive semidefinite이므로, 모든 $\lambda_i$는 양수이다. 위의 식이 0이 아니려면 각 항에 대하여 음이 아니어야 한다.
\[K^2-\lambda_i\geq0\]위 조건을 만족하는 최소값을 $K$로 선택했기 때문에 $K$가 $A^TA$의 가장 큰 고유값의 제곱근(혹은 가장 큰 특이값)임을 알 수 있다. 따라서 선형 함수의 립시츠 상수는 가장 큰 특이값이다!
쉽게 말하면 matrix $A$의 L2 norm이 A의 Largest singular value로 나타난다.
또한 일반적인 미분 가능한 함수 $f$의 립시츠 상수가 그 정의역에 대한 그래디언트의 spectral norm의 최댓값임을 알 수 있다.
\[\vert\vert f\vert\vert_{Lip} = \sup\limits_{x}\sigma(\nabla f(x))\]립시츠 함수의 속성을 사용하여 네트워크의 립시츠 상수가 각 레이어의 립시츠 상수의 곱임을 알 수 있음.
\[f(\mathbb x) = (\phi_l\ \circ\ \phi_{l-1}\ \circ\ \cdot\cdot\cdot\ \circ\ \phi_1)(\mathbb x)\]- $f_1\ is\ k_1-Lipschitz$, $f_2\ is\ k_2-Lipschitz $ 이면 $k_1k_2-Lipschitz$ 함수로 표현 가능
- $k_1,k_2$가 각각 최상의 $Lipschitz$상수인 경우에도 $(f_2\ \circ\ f_1)$의 최적의 $Lipschitz$상수는 아님
위 성질을 이용해서 다음과 같이 표현할 수 있음.
\[L(f)\leq \prod\limits_{i=1}^l L(\phi_i)\]즉 네트워크의 최적의 립시츠 상수는 레이어 개별의 립시츠 상수의 곱을 supremum으로 가짐.
하이퍼 파라미터 $\lambda$를 선택하고 이를 사용하여 각 레이어의 립시츠 상수의 상계를 제어합니다. 이는 네트워크 전체가 $\lambda^d$보다 작거나 같은 립시츠 상수를 가질 것임을 나타내며, d는 네트워크의 깊이이다.
정리하면 f의 Lipschitz norm을 이렇게 표현할 수 있다.
\[\vert\vert f\vert\vert_{Lip} = \sup\limits_{x}\sigma(\nabla f(x)) = \sup\limits_x\sigma(W) = \sigma(W)\]위의 선형의 예시처럼 $f$의 Lipschitz norm은 단순히 $W$의 Largest singular value값으로 나타난다.(또한 $f$ 그래디언트에 대한 spectral norm!)
직관을 좀 써보자.. 미천한 인간이 추상적인 개념을 이해하기 위해선 직관이 필수이다..
일단 그래디언트의 정의는 변화가 가장 큰 쪽을 나타내는 방향와 그 값일 것이다.
그렇다면 우리가 앞서 계속 설명했던 특이값(가장 큰 특이값)은 직관적으로 그래디언트와 어떤 연관성이 있어 보인다.(SVD에서 특이값을 늘릴수록 원본 이미지와 비슷해지는 것을 떠올려보자.)
즉, 레이어의 행렬 곱 부분의 Lipschitz norm은 각 레이어의 행렬 $W$의 spectral norm(가장 큰 특이값)이 될 것이다.
Spectral norm 논문에서는 $f$의 립시츠 상수인 $\sigma(W)$로 나누어서 $W$의 spectral norm이 1이되도록 정규화 해준다.
\[W_{SN}(W):=W/\sigma(W)\]모든 레이어에 대해 spectral normalization에 대해 나눠주면 (가장 큰 그래디언트쪽? 혹은 가장 큰 특이값?에 대해 나눠주자!) $f$의 Lipshitz norm이 1이하로 bounded 된다.
아무튼 이게 핵심 정리이고, 논문에서는 이를 어떻게 연산할 것인지(SVD를 계산해야 뭘 하든 할테니..) 말해주는데 그 부분은 다 읽지 못했다.
우선 핵심만 말하면 가장 큰 그래디언트(가장 큰 특이값)쪽 에 대해 보정을 해준다는 것은 레어이에서 일아는 연산이 너무 한 가지 방향으로만 급격하게 변하는 것을 막아준다.(안정적이다.)
Interaction with Dropout
드롭 아웃은 트레인때 베르누이 확률 변수의 벡터 point wise 곱을 통해 훈련 중에 활성화를 손상시킨다. 그러나 테스트 타임에는 다시 확장하는 방식으로 볼 수 있는데, 이러한 테스트 타임의 활성화를 스케일링 하는 것은 아핀 변환 레이어에서 가중치 행렬을 스케일링 하는 것으로 볼 수 있다.
너무 추상적인데…
활성화는 어쨋든 특정 값들을 어떤 구간내에 값으로 변환시켜주는 건데 이 값을 변화시킨 다는 의미는 애초에 활성화 이전의 연산되어야할 가중치를 변환시키는 것과 동일하다는 의미로 해석했다.
정의에 따라 드롭아웃은 operator norm을 스케일하고, 그러므로 해당 레이어의 립시츠 상수를 스케일 하는 것과 동일하다.

Comments