NAS

04 Aug 2020 | Auto ML

Neural architecture search with reinforcement learning

AutoML의 대표적인 테크닉인 Nas논문입니다.

중간에 reinforcement learning에 관련한 policy gradient가 나와서 읽을까 말까 고민하다가 안읽으면 계속 피하게 될 것 같아서 읽기로 결심했습니다.

덕분에 강화학습 공부 했습니다… policy gradient 1

policy gradient 2

2018 CVPR에 발표된 논문이고, RNN을 사용하여 모델의 description을 생성하고 강화 학습을 사용하여 RNN을 학습한 뒤 validation set에서 생성된 아키텍처의 predict accuracy를 최대화 합니다.

논문의 특징으로는 GPU 800장과 한달이 필요하며(???), CIFAR-10데이터를 사용합니다.

결국 AutoML을 통해 모델 아키텍처를 모델이 설계 가능함을 보였습니다.

AutoML

AutoML이 뭔지 가볍게 알아봅시다.

아주 직관적으로 말하면 머신 러닝 모델을 설계하는 머신 러닝 모델입니다.

조금 더 자세히 말해보자면 데이터로부터 모델을 학습하고, 배포하여 예측하는 전체 파이프 라인을 자동화 하는 것입니다.

저희 밥그릇을 위협하는 무시무시한 기술입니다.. :(

AutoML은 크게 3가지 방향으로 연구가 진행되고 있습니다.

  • Automated Feature Learning
  • Architecture Search
  • Hyperparameter Optimization

본 논문은 Architecture Search와 관련이 있습니다.

기존의 ML에서 feature engineerings을 hands-craft로 하던 feature design에서 DL로 넘어오면서 architecture design으로 변경됐습니다. 물론 featrue design보다는 쉽지만, 여전히 architecture design도 어렵습니다. 이걸 자동화 할 순 없을까? 라는 생각에서 Architecture search는 출발합니다.

Introduction

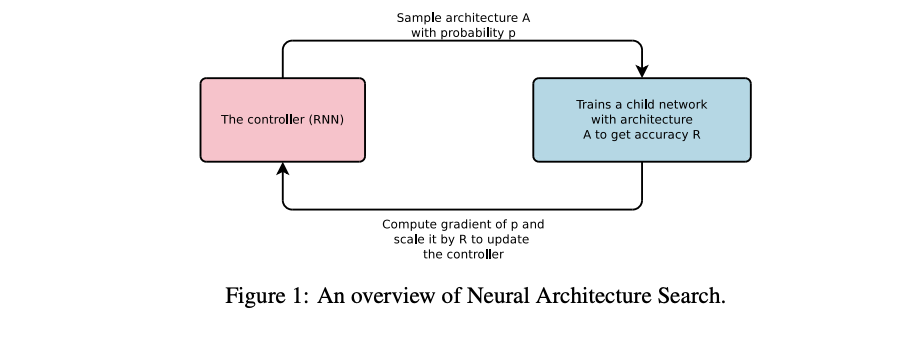
기본 아이디어는 다음과 같습니다.

  • RNN Controller를 통해 child network를 만든다.
  • CIFAR-10으로 validation accuracy가 수렴할 때 까지 child를 학습한다.
  • 수렴한 accuracy를 reward로 설정하여 reward의 기댓값을 높이는 방향으로 controller를 학습한다.

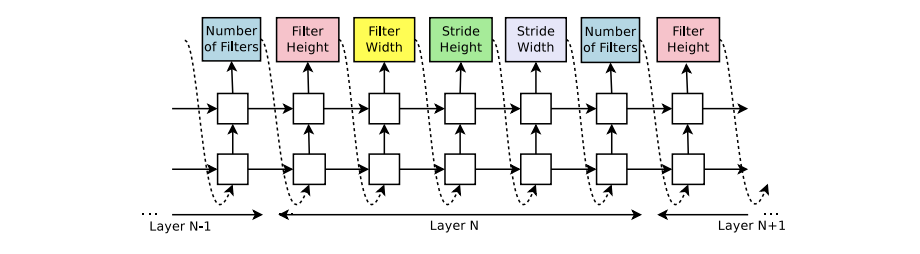
Controller는 하이퍼 파라미터를 결정합니다.

  • filter height in [1, 3, 5, 7]
  • filter width in [1, 3, 5, 7]
  • number of filters in [24, 36, 48, 64]
  • strides in [1, 2, 3] (or 1)

위 값을 모두 결정하면 하나의 Conv레이어가 완성되고, 이를 N번 반복하여 N개의 서로 다른 레이어를 생성합니다. Controller를 RNN으로 만든 이유는 이전의 선택 결과에 영향을 받기 위해서 입니다.

뭔가 grid search, random search가 떠오르기도 합니다.

사실 저런 것들이 모델을 잘 만드는 길을 찾는 과정이라면 강화학습이 제일 잘하는 분야이니까 강화학습을 사용한게 납득이 갑니다.

아키텍처 생성을 마치면 신경망을 만든 뒤 훈련이 시작됩니다. 네트워크가 수렴하면, validation set에서 정확도를 기록하고 RNN의 파라미터 $\theta_c$는 제안된 아키텍처의 예측 검증 정확도를 최대화 하기 위해 업데이트 됩니다.

그런데.. 이 $\theta_c$를 업데이트 하는 과정이 좀 무시무시합니다.

천천히 살펴봅시다..(수식주의)

Training with Reinforce

컨트롤러가 예측하는 하이퍼 파라미터 리스트들은 하위 네트워크 아키텍처를 설계하기위한 액션들의 목록 $a_{1:T}$ 로 볼 수 있습니다.

이 액션의 연속으로 나온 것이 하위 네트워크이며, 최종 출력인 validation set에 대한 수렴 accuracy $R$을 얻을 수 있습니다. 이 $R$을 보상으로 하여 RNN 컨트롤러에 강화학습을 진행합니다.

\[J(\theta_c) = E_{p_{(a_{1:T};\theta_c)}}[R]\]

$R$이 non-differentiable이기 때문에 policy gradient를 사용해야 합니다.

\[\nabla_{\theta_c}J(\theta_c) = \sum\limits_{t=1}^TE_{p_{(a_{1:T};\theta_c)}}[\nabla_{\theta_c}logP(a_t\vert a_{(t-1):1};\theta_c)R_k]\]

뭔가 갑자기 확 넘어간 느낌입니다. 조금 자세히 알아봅시다.

Policy

우선 일반적인 policy의 목적함수는 다음과 같습니다.

\[J_{avR}(\theta) = \sum_sd^{\pi\theta}(s)\sum_a\pi\theta(s,a)R^a_s\]

주어진 policy $\pi\theta(s,a)$가 있을 때 최적의 $\theta$를 찾는 문제입니다. 여기서 최적의 $\theta$는 당연히 보상이 클 때를 얘기하겠죠?($d^{\pi\theta}$ : stationary disrtribution)

어쨋든 저희에게 익숙한 최적화 문제고 이를 Gradient Descent로 풀게 되면 바로 저희가 하려는 Policy Gradient 방법입니다.

Monte-Carlo Policy Gradient

몬테-카를로 방법은 에피소드 단위로 policy를 업데이트합니다.

policy의 목적 함수 Gradient를 계산하려면 다음 식을 계산할 수 있어야 합니다.

\[\sum\limits_{s\in S}d(s)\sum\limits_{a\in A}\nabla_{\theta}\pi_{\theta}(s,a)R_{s,a}\]

하지만 $\pi_{\theta}$라는 확률 함수가 없기 때문에 행동을 취할 수 없습니다. 다르게 표현하면 Policy함수에 대한 sampling을 할 수 없기 때문에 기댓값을 구할 수 없습니다.

이를 해결하기 위해 다음 관계를 이용하여 목적 함수의 Gradient를 구합니다.

\[\nabla_{\theta}\pi_{\theta}(s,a) = \pi_{\theta}(s,a)\frac{\nabla_{\theta}\pi_{\theta}(s,a)}{\pi_{\theta}(s,a)}\] \[=\pi_{\theta}(s,a)\nabla_{\theta}log\pi_{\theta}(s,a)\]

이를 통해 다음과 같은 표현이 가능해집니다.

왜 하는지 모르겠으면 기댓값에 정의에 대해 생각해봅시다.

$\nabla_\theta E[f(x)] = \nabla_\theta \int p_\theta(x)f(x)dx \ = \int \frac{p_\theta(x)}{p_\theta(x)}\nabla_\theta p_\theta(x)f(x)dx\ = \int p_\theta(x)\nabla_\theta logp_\theta(x)f(x)dx\ = E[f(x)\nabla_\theta log p_\theta(x)]$

\[\nabla_{\theta_c}J(\theta_c) = \sum\limits_{s\in S}d(s)\sum\limits_{a\in A}\pi_{\theta}(s,a)\nabla_{\theta}log\pi_{\theta}(s,a)R_{s,a} = E_{\pi_{\theta}}[\nabla_{\theta}log\pi_{\theta}(s,a)r]\]

여기서 $\nabla_{\theta}log\pi_{\theta}(s,a)$를 score function이라고도 부릅니다.

멀리 돌아왔습니다. Monte-Carlo Policy gradient를 통해 $\nabla_{\theta_c}J(\theta_c) = \sum\limits_{t=1}^TE_{p_{(a_{1:T};\theta_c)}}[\nabla_{\theta_c}logP(a_t\vert a_{(t-1):1};\theta_c)R_k]$를 유도할 수 있습니다.

m개의 샘플을 하나의 배치로 한 번에 업데이트 하고자 하는 경우 아래와 같이 근사가능합니다.

\[\frac1{m}\sum\limits_{k=1}^m\sum\limits_{t=1}^T\nabla_{\theta_c}logP(a_t\vert a_{(t-1):1};\theta_c)R_k\]

$R_k$는 k번 째 child network로 부터 얻은 validation accuracy입니다. 단 위 식으로 학습할 경우 variance가 매우 커질 수 있기 때문에 baseline function을 사용한 다음 식을 사용합니다.

\[\frac1{m}\sum\limits_{k=1}^m\sum\limits_{t=1}^T\nabla_{\theta_c}logP(a_t\vert a_{(t-1):1};\theta_c)(R_k-b)\]

논문에서 $b$는 이전 아키텍처의 평균 accuracy를 이용하여 결정합니다.

저희가 쓰는 방법은 REINFORCE(Monte-Carlo Policy Gradient)라는 방법인데, 이 방법은 에피소드의 샘플 내에서 몬테-카를로 방법을 통해 구한 estimation return을 가지고 policy parameter $\theta$를 업데이트 해 나갑니다. REINFORCE는 샘플 내에서 gradient에 대한 기댓값이 actual 내에서의 gradient에 대한 기댓값과 같기 때문에 효과가 있습니다. 다음 식을 봅시다.

\[\nabla_\theta J(\theta) = E_\pi[Q^\pi(s,a)\nabla_\theta ln\pi_\theta(a\vert s)]\\ = E_\pi[G_t\nabla_\theta ln\pi_\theta(A_t\vert S_t)]\]

Because $Q^\pi(S_t,A_t) = E_\pi[G_t\vert S_t,A_t]$

이를 통해서 랜덤 샘플 trajectory들로 부터 total expected return $G_t$를 구할 수 있게 되었고, 이를 이용해서 policy gradient를 업데이트 할 수 있습니다. 이 때 전체 trajectory를 활용하게 되고, 이 때문에 Monte-Carlo Method라고 부른다고 합니다.

  • policy parameter $\theta$를 랜덤하게 지정합니다.
  • 해당 policy parameter $\theta$를 가진 policy $\pi_\theta$를 통해서 trajectory를 생성합니다.($S_1,A_1,R_1, S_2,A_2,R_2,…$)
  • $t=1,2,…,T$에 대해서
    • Total expected return $G_t$를 추정합니다.
    • 이를 바탕으로 Policy parameter를 업데이트합니다 ($\theta \leftarrow \alpha\gamma^tG_t\nabla_\theta ln\pi_\theta(A_t\vert S_t)$)

Accelerate Training with Parallelism and Asynchronous Updates

Nas에서 컨트롤러의 파라미터 $\theta_c$에 대한 각 Gradient 업데이트는 하나의 네트워크를 수렴하도록 훈련시키는 것입니다.

하위 네트워크를 교육하는 데 시간이 오래 걸리므로 분산 학습및 비동기 업데이트를 사용하여 학습 속도를 높입니다.

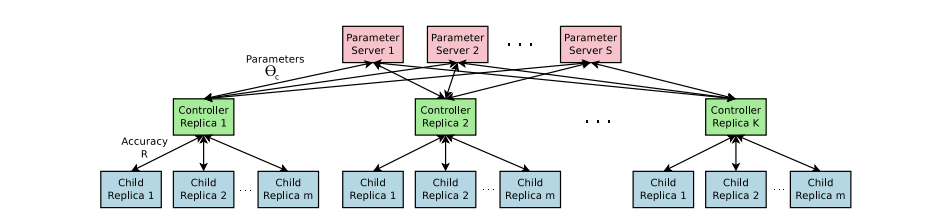
컨트롤러의 파라미터를 저장하는 파라미터 서버가 $S$개 존재하며, 이 서버들은 $K$개의 컨트롤러에게 파라미터를 보냅니다. 이를 통해 컨트롤러들은 m개의 아키텍처를 생성하고, 이를 병렬적으로 학습시켜 최종 Gradient를 계산합니다. 그 뒤 이를 다시 파라미터 서버에 보내며 업데이트 시킵니다. 이 과정을 epoch만큼 반복합니다.

Increase Architecture Complexity with Skip Connections and Other Layer Type

위 그림에서 알 수 있듯, 컨트롤러의 search space은 Skip connection과 같은 최신 아키텍처에 사용되는 기법들을 탐색하지 못합니다. 이를 위해 search space를 넓혀서 컨트롤러가 이런 기법들에 대해서도 제안할 수 있도록 하는 방법을 소개합니다.

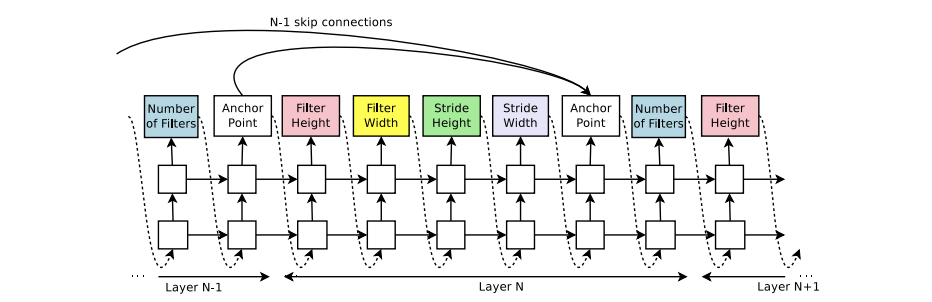
커넥션을 위해서 set-selection attention을 사용합니다. 각 레이어에는 앵커 포인트가 생기는데, 현재 레이어가 N일 때 이전 레이어에서 연결 할지 말지를 계산합니다.

\[P(j\rightarrow i) = sigmoid(v^T tanh(W_{prev}*h_j+W_{curr}*h_i))\]

$i\rightarrow j$: 레이어 $j$가 레이어 $i$에 대한 인풋

$h_j$: $j$ 번째 레이어의 앵커 포인터에서 컨트롤러의 히든스테이트

$W,v$: trainable parameter

이러한 연결은 확률 분포에 의해 정의되고, 기존의 순차적인 연결이 아닌 앵커를 통해서 레이어들이 연결되는 것으로 바뀔 뿐 reinforce방법은 수정 없이 사용 가능합니다.

다만 이런 커넥션을 추가할 때 문제가 발생할 수도 있습니다.

예를 들어, 하나의 레이어에 많은 레이어가 인풋으로 들어오게 될 때, 많은 레이어를 concatenation하여 인풋으로 사용하게 되는데 이럴 때 차원 관련 문제가 생길 수 있고 혹은 레이어의 인풋이 없는 경우가 발생할 수 있습니다. 따라서 논문에서는 세 가지 방법을 추가로 적용해서 사용합니다.

  • 레이어에 인풋이 없는 경우 이미지를 인풋으로 넣습니다.
  • 최종 레이어는 아웃풋 레이어가 없는 모든 레이어를 연결합니다.
  • 만약 인풋 레이어들 끼리 다른 사이즈를 가지고 있다면, 작은 레이어는 패딩을 적용하여 같은 사이즈로 만듭니다.

위 뿐만 아니라, learning rate, pooling, normalization, batch normalization도 가능합니다. 필요한 작업은 컨트롤러가 레이어 타입을 출력하게 만들면 된다고 합니다.

Generate recurrent cell architecture

위 방식을 수정하여 RNN cell을 만들어 봅시다.

기본적인 rnn모델은 히든 스테이트 $H_t$를 입력값 X와 이전 출력값 $H_{t-1}$을 이용하여 계산합니다.

\[H_t = tanh(W_1*x_t + W_2*h_{t-1})\]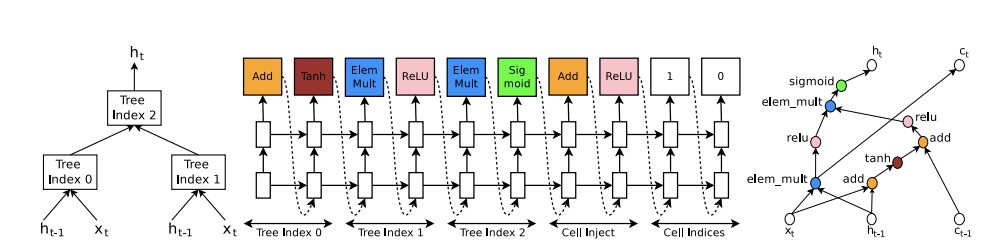

하이퍼 파라미터들을 출력한다는 점에서 이전 Nas와 동일하지만, 레이어 별로 하이퍼 파라미터를 출력하는 것이 아니라, 필요한 연산들을 트리 구조로 나타내어 하이퍼 파라미터를 출력합니다. 위 그림에서 왼쪽 트리는 기본적인 RNN의 틀을 만들어준 트리입니다.

각 트리의 노드마다 계산 방법과 활성화 함수를 Nas모델이 출력하게 됩니다.(위 그림처럼 LSTM의 경우 cell state를 활용) 이렇게 복잡한 경우 RNN 모델을 표현하기 부족할 수 있기 때문에 추가적으로 cell inject와 cell indices부분을 받습니다.

cell inject는 cell state가 사용할 계산 방법과 활성화 함수를 출력하는 부분이며 cell indices는 각각의 cell state가 기존의 트리 노드에 끼어들 부분을 선택하는 부분입니다.

Experiments

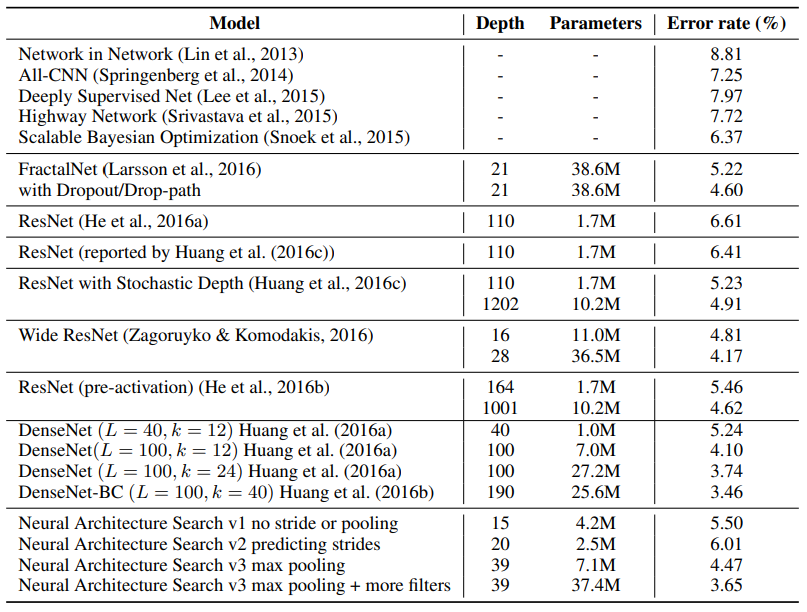
기존의 가장 좋은 성능인 DenseNet과 유사하다는 것을 볼 수 있습니다. 이를 통해 Nas를 통한 architecture search가 어느정도 가능함을 보여주고 있습니다. 표를 더 자세히 보면 Nas 내부적으로도 하이퍼 파라미터, 레이어를 통해 성능을 더 높일 수 있습니다.v2의 경우를 자세히 보면 stride를 예측하게 만드는 것이 오히려 성능을 떨어지는데, 이는 search space가 넓어지게되어 컨트롤러에 악 영향을 끼친 것으로 파악됩니다.

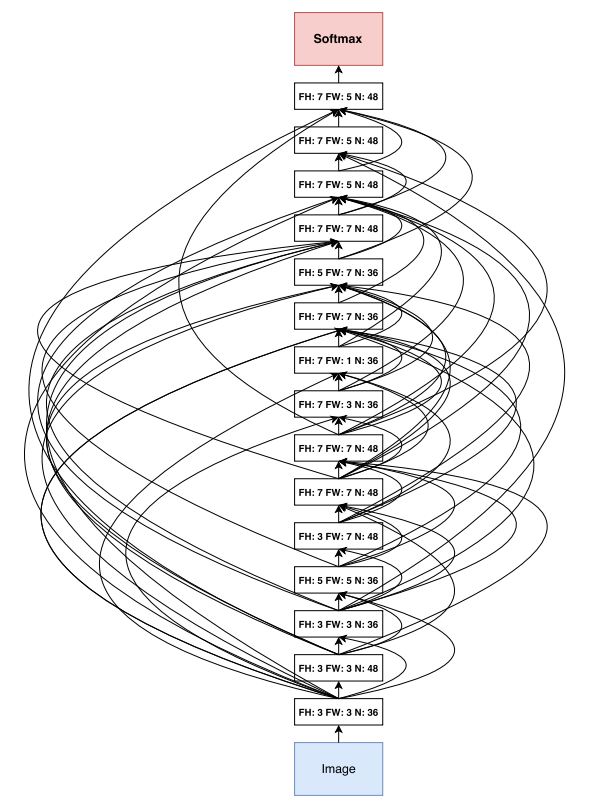
Conclusion

새로운 태스크의 논문을 읽어보고싶어서 선정했는데 강화학습을 더 공부해야 할 것 같습니다. meta-learning, Auto-ML은 제가 생각한 것 보다 훨씬 백그라운드가 많이 필요하지만 그만큼 재밌는 부분이 많은 것 같습니다.

본 논문에서 한가지 배운 점은 지나친 자유도는 성능이 좋지 않다는 점입니다.

v2모델의 성능이 떨어진 것 처럼 search space가 넓어 질수록 성능이 오히려 떨어지니까요, 이 논문을 시작으로 많은 Nas를 응용한 연구들이 진행된 것으로 아는데 후속 논문(NASNet)도 이런 자유도에 대한 제약을 줘서 학습 시간을 단축시키고 성능을 많이 높였다고 합니다.

또한 RNN을 통해서 신경망 아키텍처를 찾아내는 아이디어는 굉장히 신선한 것 같습니다.

Paper link

Paper Review

Policy gradient

발표용 ppt

Related Posts

Comments