Unsupervised Learning of Visual Representations by Solving Jigsaw Puzzles

Abstract

이 논문에서는 label 없이 image representation 학습의 문제에 대해 연구합니다.

Self Supervised 원칙을 준수하여 Pretext task로 직소 퍼즐을 풀도록 훈련할 수 있는 CNN을 구축합니다.

수동으로 라벨링이 필요하지 않으며 나중에 객체 분류 와 객체 감지를 해결하기 위해 용도를 변경했습니다.

여러 작업에서 호환성을 유지하기 위해 siamese-ennead CNN인 Context Free Network(CFN)을 소개합니다.

siamese 네트워크란? 두 이미지를 입력으로 받아서 두 이미지를 벡터화 시킨 후 두 벡터간의 유사도를 반환하는 네트워크

네트워크는 이미지의 feature를 데이터에서 직접 학습하므로 유사도를 최적화 할 수 있는 feature를 추출해준다.

CFN은 이미지 타일을 입력으로 사용하고

직소 퍼즐을 풀기 위해 CFN을 훈련시킴으로써, 모델은 객체 부분의 특징 매핑과 공간 배열을 배웁니다.

Visual representation을 위해 제안된 방법은 여러 transfer learning 벤치 마크에서 SOTA 방법보다 우수합니다.

Introduction

우리는 디텍션 및 분류 작업으로 transfer될 때 높은 성능을 제공하는 features를 구축하는 새로운 Self Supervised task인 직소 퍼즐 재조립 문제를 소개합니다.

논문은 직소 퍼즐을 푸는 것이 객체가 어떤 부분(parts)로 구성되어 있고 이 parts가 무엇인지 모델을 가르치는데 사용될 수 있다고 주장합니다.

단순히 말해서 jigsaw puzzle이 이 논문에서 pretext task라고 말하는 것 같습니다.

각각의 개별 퍼즐 타일과 정확한 물체 부분의 연관성은 모호할 수 있습니다.

그러나 모든 타일이 관찰되면 타일 배치가 mutually exclusive이므로 모호성이 쉽게 제거될 수 있습니다.

Related Work

우리 작업은 representation/ feature learning에 속하며 이는 Unsupervised learning입니다.

Representation learning은 머신 러닝의 작업을 해결하는데 유용한 데이터의 intermediate representation을 구성하는 것과 관련이 있습니다.

또한 직소 퍼즐을 사용하여 객체 분류 및 디텍션와 같은 다른 작업을

해결함으로써 새로운 기능을 적용하고 용도를 변경함에 따라 transfer learning도 포함됩니다.

우리의 실험은 이전 연구에서 처럼 사전 학습 + 미세 조정을 사용합니다.

사전 학습은 직소 퍼즐을 해결하면서 얻은 features에 해당하고,

미세 조정은 다른 작업(객체 분류 및 감지)을 해결하기 위해 사전 학습에 얻은 가중치를 업데이트하는 과정입니다.

Unsupervised Learning.

대부분의 기술들은 범용적인 목적의 prior(사전 정보..?)를 이용하여 표현을 구성합니다.

안타깝게도 시각적 표현을 디자인하는 일반적인 기준은 없습니다.

그럼에도 불구하고, 자연스러운 선택은 factor of variation의 분리를 목표로 하는 것입니다.

예를들어 객체의 모양 같은 몇몇 factor들은, 물체와 광원이 결합되어 그림자, 음영, 색상, 패턴 및 이미지의 반사와 같은 복잡한 효과를 만듭니다.

이상적인 features는 이러한 각 factor를 분리하여 다른 학습 작업( ex: 모양 또는 표면 재료를 기준으로 한 분류)를 보다 쉽게 처리할 수 있습니다.

이 작업에서는 외형을 객체 일부의 배열(형상)과 분리하는 기능을 설계합니다.

일반적으로 Unsupervised learning methods를 Probabilistics, Direct mapping(autoencoders), Manifold learning으로 그룹화 할 수 있습니다.

Probabilistic 방법은 네트워크의 변수를 관측 및 잠재 변수로 나눕니다.

학습은 관측치가 주어진 잠재 변수의 likelihood를 최대화 하는 모델 파라미터를 결정하는 것과 연관됩니다.(ex: RBM)

불행히도 이러한 모델은 다중 레이어가 존재할 때 다루기 어려워지며 효율적인 방식으로 형상을 생성하도록 설계되지 않았습니다.

애초에 위에서 likelihood를 최대화 한다는게 MLE를 말하는 것 같은데 likelihood 모델이 조금만 복잡해져도 intractability 해지는 것은 자명합니다.

Direct mapping 방식은 latter aspect에 초점을 맞추고 일반적으로 오토인코더를 통해 구축되고,

오토 인코더에 의해 생성된 입력과 출력 사이의 reconstruction error를 최소화 함으로써 학습됩니다.

Manifold learning방식은 데이터 구조를 통해 데이터 포인트가 매니폴드 주위에 집중될 수 있다고 제안하면 manifold learning 기법을 사용할 수 있습니다.

매니폴드는 국부적으로 저차원의 유클리디안 거리로 볼 수 있는 고차원 공간을 말합니다.

사실 표현 학습의 강점은 샘플을 묘사하는데 가장 뛰어난 특성과 이런 특성을 원본 데이터에서 추출하는 방법을 학습하는 것입니다.

이를 수학적으로 말하면 데이터의 비선형 매니폴드를 찾고 공간을 완전하게 설명하기 위해 필요한 차원을 구성합니다.

Self-supervised Learning.

이 학습 전략은 데이터와 함께 “무료”로 제공되는 라벨링을 활용하는 Unsupervised learning의 최신 변형 버전입니다.

이 라벨링은 크게 두 가지로 구분됩니다.

1. Non-visual 신호와 연관되고 쉽게 얻을 수 있는 label(ex. Ego-motion, audio, text)
2. 데이터 구조로 부터 얻을 수 있는 label

우리는 단순히 입력 이미지를 재사용 하고 픽셀 배열을 레이블로 활용하기 때문에, 후자와 관련이 있습니다.

• Doersch 방식은 두 개의 이미지 패치 사이의 상대적 위치를 분류합니다.

  이 방식의 3x3 그리드 이미지에서 중간 타일이 고정되고 나머지 한 타일이 대각선에 위치할 경우 위치 파악이 어려운 단점이 있습니다.

  하지만 우리 방식은 모든 타일을 동시에 관찰하고 이를 통해 훈련된 네트워크는 이러한 어려움을 줄일 수 있습니다.

• Wang & Gupta 방식은 패치들 사이의 유사성을 정의하는 metric을 구축합니다.

  3개의 패치가 입력으로 사용되며 여기서 2개의 패치는 비디오 트래킹을 통해 동일한 물체로 부터 가져오고 나머지 한 개는 임의로 선택됩니다.

  이 방식의 장점은 라벨링에 tracking method만 사용한다는 것입니다.

• Agrawal 방식은 다른 센서가 제공하는 라벨링(ego-motion)을 이용합니다.

  이 라벨링은 대부분의 경우 자유롭게 사용할 수 있거나 쉽게 얻을 수 있다는 장점이 있습니다.

  두 개의 이미지 프레임에서 ego-motion을 추정하고 odometry 센서로 측정한 ego-motion과 비교하기 위해 siamese 네트워크를 훈련시킵니다.

  동일한 물체의 다른 이미지를 사용하면 학습된 features들은 high-level이 아닌 유사성(ex: color & texture)에 중점을 둡니다.

대조적으로 직소 퍼즐 방식은 타일의 color & texture와 같은 localization에 도움이 되지 않는 low-level 유사성을 무시하고, 패치간의 차이에 초점을 맞춥니다.

다른 모델이라면 아래의 차와 개는 같은 카테고리이며 color와 texture만 다르니까 같다 라고 표현하겠지만,

CFN은 다르다고 표현합니다.

Jigsaw Puzzles

직소 퍼즐은 예전부터 아이들의 학습에 이용되었기 때문에 근본적으로 학습과 관련이 있습니다.

심리학적 연구에 따르면 직소 퍼즐을 사용하여 사람의 가상 공간 처리를 평가할 수 있습니다.

논문에서는 직소 퍼즐을 사용하여 사람의 가상 공간 처리 능력을 평가하는 대신 CNN과 관련하여 객체의 가상 공간 표현을 개발하기 위해 직소 퍼즐을 사용합니다.

계산적으로 직소 퍼즐을 푸는 것에 접근하는 논문은 많습니다.

그러나 이런 방법들은 타일의 형상 또는 타일 경계에 근접한 texture에 의존합니다.

이러한 단서들은 part detector를 학습할 때 유용한 정보를 가지고 있지 않기 때문에 직소 퍼즐을 풀기 위한 모델을 훈련 시킬 때는 피해야 할 신호입니다.

Solving Jigsaw Puzzles

여기서는 범용 features를 배우면서 직소 퍼즐을 풀 수 있는 CNN 구조에 어떻게 도달했는지 간략하게 설명합니다.

직소 퍼즐을 해결하기 위한 즉각적인 접근 방식은 채널을 따라 퍼즐 타일을 쌓은 다음 (즉, 입력 데이터는 9x3 = 27 채널) AlexNet에서 첫 번째 필터의 깊이를 증가시키는 것입니다.

하지만 이 방식은 네트워크가 low-level 유사성을 배우도록 했기 때문에 다른 방식을 사용합니다.

low level을 이토록 싫어하는 이유?

최종 목표는 직소 퍼즐이라는 pretext task를 통해 representation을 학습한 네트워크를 사용해서 다른 visual task에 적용할 것인데

결과적으로 pretext를 통해 직소 퍼즐을 푸는 것 뿐만 아니라 그 과정에 있어서 이미지 그 자체에 대한 정보와 객체에 대한 정보를 모델이 캐치해야 합니다.

하지만 low-level 을 학습하게 되면 글로벌 객체에 대한 이해없이도 문제를 풀기 때문에 우리가 최종적으로 하려는 목표에 부합하지 않게 됩니다.

따라서 여러 타일에 대한 통계 계산을 지연시키는 네트워크를 제시합니다.

네트워크는 먼저 각 타일 내의 픽셀만을 기준으로 feature를 연산합니다.

그런 다음 이러한 feature를 사용하여 parts들의 배열을 찾습니다.

목표는 상대 위치를 결정하기 위해 네트워크가 각 객체 부분에서 가능한 대표적이고 구별 가능한 features를 학습하도록 하는 것입니다.

학습 시에 이미지에서 225x225의 이미지를 무작위로 crop하고 이를 3x3 grid로 나눈 뒤 각 grid에서 무작위로 64x64로 crop한 것을 하나의 타일로 이용해 총 9개의 타일을 만듭니다.

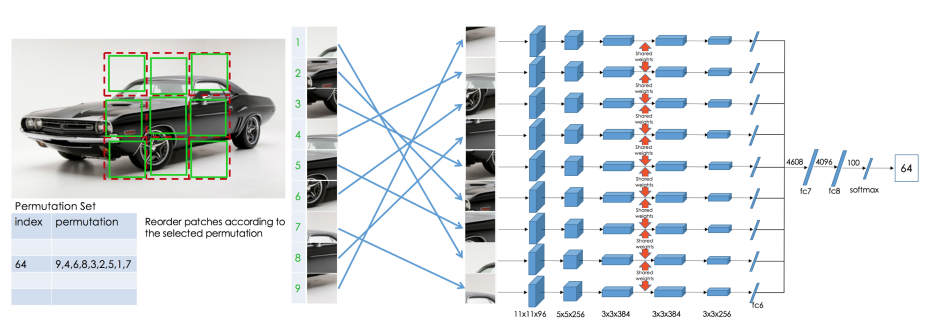
그리고 이 타일을 사전 정의된 순서 집합중 하나에 따라 재 정렬 후 네트워크의 입력으로 넣습니다.

The Context-Free Architecture

우리는 siamese-ennead CNN을 구축합니다.

첫 번째 완전 연결층(fc6)까지의 각 행은 공유 가중치와 함께 AlexNet 구조를 따릅니다.

모든 층의 출력은 연결되어 fc7의 입력으로 제공됩니다. Fc6를 포함한 행의 모든 레이어는 동일한 가중치를 공유합니다.

이러한 구조를 CFN(Context Free Network)라고 부릅니다.

왜냐하면 fc7전까지 각각 입력으로 들어간 패치들은 서로에게 영향을 받지 않고(context-free) feature를 학습하고 fc7에서 만나기 때문입니다.

Fc7에서 만난 feature들은 각 parts의 배열을 결정하는데 사용됩니다.

테스트 시에는 학습할 때와 다르게 이미지 전체를 225x225로 resize하고 각 grid에서 무작위로 crop하지 않고 전체 75x75를 씁니다.

결과적으로 AlexNet보다 적은 파라미터를 가지고 비슷한 성능을 이끌어 냈습니다.

The Jigsaw Puzzle Task

CFN을 훈련시키기 위해 타일 구성 S= (3, 1, 2, 9, 5, 4, 8, 7, 6)과 같은 직소 퍼즐의 순열을 정의하고 각 항목에 index를 할당합니다.

CFN이 각 인덱스의 확률값을 벡터로 반환하도록 학습시켰습니다.

타일이 9개니까 9! = 362,880 개의 경우가 나옵니다.

실험을 통해 순열 집합이 네트워크가 학습하는 표현의 성능에 중요한 요소라는 것을 알게됐습니다.

Training the CFN

CFN의 출력은 객체의 일부분을 공간적으로 배치하는 조건부 PDF로 볼 수 있습니다.

$p(S\vert A_1,A_2, … ,A_9) = p(S\vert F_1, F_2, …,F_9) \prod\limits_{i=1}^{9}p(F_i\vert A_i) \tag{1}$

여기서 $S$는 타일의 구성이고, $A_i$는 객체의 $i$번째 parts의 모양이며 ${F_i}_{i=1,…9}$ 는 intermediate feature representation 입니다.

우리의 목적은 features $F_i$가 parts들 사이의 상대적 위치를 식별할 수 있는 의미적 속성을 갖도록 CFN을 훈련시키는 것입니다.

한 가지 문제는 CFN이 각 모양 $A_i$를 절대 위치에 연관시키는 것을 배우는 경우입니다.

이 경우 $F_i$는 의미있는 속성을 가지지 않고 임의의 2D 위치에 대한 정보만 가질 것입니다.

이미지 당 하나의 직소 퍼즐($S$)만 생성하면 위 같은 문제가 발생할 수 있습니다.

그렇게 되면 CFN은 texture/structural 컨텐츠가 아니라 퍼즐의 절대 위치를 기반으로 패치를 클러스터링하는 방법을 배웁니다.

타일 위치 $S = (L_1,…L_9)$의 목록으로 구성 $S$를작성하면 조건부 PDF $p(S\vert F_1,F_2,…,F_9)$는 독립항으로 분해됩니다.

$p(L_1,…,L_9\vert F_1, … ,F_9) =\prod\limits_{i=1}^{9}p(L_i\vert F_i) \tag{2}$

여기서 각각 타일의 위치 $L_i$는 대응하는 특징 $F_i$에 의해 결정됩니다.

일반적으로 SSL은 pretext task를 해결하기에는 적합하지만 target task(객체인식, 분류 등..)는 해결하지 못하는 표현으로 이어질 수 있습니다.

이와 관련하여 더 나은 표현을 배우기 위한 중요한 요소는 우리의 모델이 pretext task를 해결하기 위해 바람직하지 않은 솔루션을 취하는 것을 방지하는 것입니다.

이러한 솔루션을 “shortcuts” 라고 합니다.

shortcuts는 위에서 언급했던 절대위치, color & texture와 같은 low-level similarity 등이 있겠죠?

shortcuts를 피하기 위해 여러가지 기술을 사용합니다.

• 이미지가 절대적인 위치를 학습하는 것을 피하기 위해 이미지당 1000개의 배치중 평균적으로 69개의 배치를 사용했고, 각 배치들은 평균적으로 충분히 큰 Hamming distance를 가지도록 선택했습니다.
• 경계 연속성과 픽셀 강도 분포로 인한 shortcuts를 피하기 위해 타일 사이에 임의의 간격을 남겨 둡니다.(평균 11픽셀)
• chromatic aberration로 인한 지름길을 피하기 위해 color channel jittering을 위해 그레이 스케일 이미지가 사용됩니다.

Implementation Details

Batch-norm을 사용하지 않고 SGD를 사용했습니다.

256x256 크기의 1.3M개 컬러 이미지와 batch-size = 256을 사용합니다.

학습동안에는 한 이미지당 평균 69개의 직소 퍼즐을 풉니다.

Experiments

transfer learning에서 성능을 평가하고, ablation study를 수행하고, 중간층의 뉴런들을 시각화하고, 다른 방법들과 비교합니다.

Transfer Learning

PASCAL VOC 데이터 셋으로 분류 디텍션 및 시멘틱 세그멘테이션 작업을 위해 사전 훈련된 가중치로 학습된 features를 평가합니다.

또한 Unsupervised/Self-Supervised를 평가하기 위한 새로운 벤치 마크도 소개합니다.

CFN의 학습이 끝난 후 CFN의 가중치를 사용하여 AlexNet 네트워크의 모든 컨볼루션 레이어를 초기화합니다.

그런 다음 ImageNet 데이터에서 객체 분류를 위해 나머지 네트워크를 scratch로 구현합니다.(나머지 층은 정규분포 초기화)

CFN의 첫 번째 층은 stride = 2 이지만, 다른 모델과의 비교를 위해서 AlexNet에서는 stride = 4를 사용합니다.

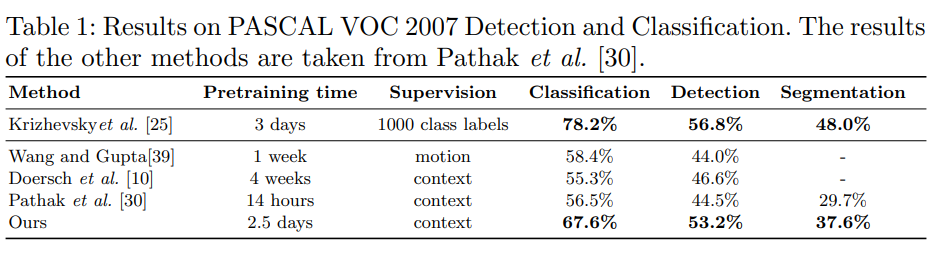
Pascal VOC 데이터 셋의 분류 작업에 대해 직소 task를 통해 얻은 feature를 fine-tuning하여 여러 프레임 워크를 통해 비교합니다.

Pathak 방식은 Context-encoder 방식.

결론은 CFN을 통해 학습한 feature들을 PASCAL VOC-2007에 적용했을 때 나머지 3개보다는 뛰어났고 AlexNet과 비슷한 성능을 보입니다.

ImageNet Classification

Yosinski 논문에서 AlexNet의 마지막 층이 훈련에 사용되는 task 및 데이터 셋에 고유한 반면 첫 번째 층은 범용적이라는 것을 보여 주었습니다.

transfer learning의 맥락에서 범용 -> 특정 작업으로의 transfer는 네트워크에서 feature를 추출해야하는 위치를 결정합니다.

이번 섹션에서는 학습된 표현이 어디서 발생하는지를 확인해보려 합니다.

첫 문장에서 말했듯이 각 레이어별로 어떤 레이어가 task에 specific이 되는지

레이어를 freeze했다가 풀면서 알아보겠다는 뜻인 것 같습니다.

아무튼 위처럼 실험하게 되면 AlexNet 기준 57.4%의 정확도를 얻습니다.

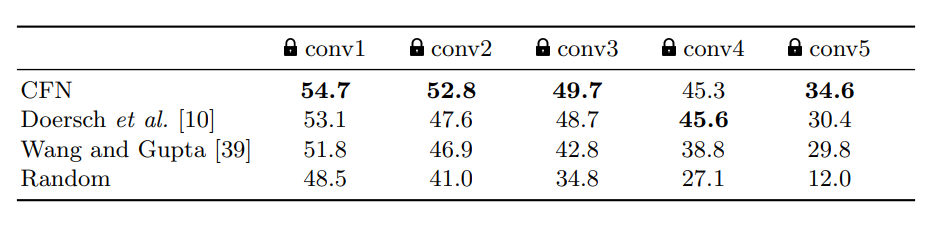
우리의 방식은 완전 연결 층만 훈련할 경우 34.6%였지만, conv5 레이어도 함께 훈련할 경우 45.3%로 크게 개선되었습니다.

이게 제가 말했던 하위 레이어가 어떤 task에 더 specific해진다는 의미인 것 같습니다.

컨볼루션 레이어는 feature extract의 느낌이 강하지만 사실상 depth에따라 역할이 다르고(실제로 알지는 못하지만)

논문에서 언급한 것 처럼 첫 번째 계층은 범용적이지만 마지막으로 갈수록 task에 specific 해집니다.

또한 우리는 semantic classification이 직소 퍼즐을 푸는데 유용한지 확인하고 객체 분류와 직소 퍼즐 재조립 작업이 얼마나 관련되어 있는지를 확인하기 위해 다음과 같이 실험했습니다.

사전 훈련된 AlexNet을 가져와서 직소 퍼즐을 풀기 위해 feature transfer를 적용합니다.

위에서 실험한 것과 동일한 방식을 사용하여 여러 레이어에서 피처의 transferbility를 확인합니다.

직소 task의 최대 정확도인 88%와 비교할 때 semantic training이 객체 parts를 인식하는데 매우 도움이 된다는 것을 볼 수 있습니다.

Ablation Studies

우리는 제안된 방법에 대한 albation studies를 수행하여 직소 task 훈련 중 각 구성 요소의 영향을 보여줍니다.

우리는 다른 순열 집합에서 학습합니다(위에 수식에서 설명한 $S$가 다양해야 합니다.)

순열 집합은 작업의 모호성을 제어합니다.

순열이 비슷하다면 직소 퍼즐 task는 더 어려워지고 모호해집니다.

예를 들어 서로 다른 순열 간의 차이가 두 타일의 위치에만 있고, 이미지에 두 개의 유사한 타일이 있는 경우 올바른 솔루션을 예측할 수 없습니다.

이미지의 유의미한 feature를 학습하지 않은 경우

비슷한 타일이 위치만 다를경우 뭐가 정답인지 알 수 없겠죠?

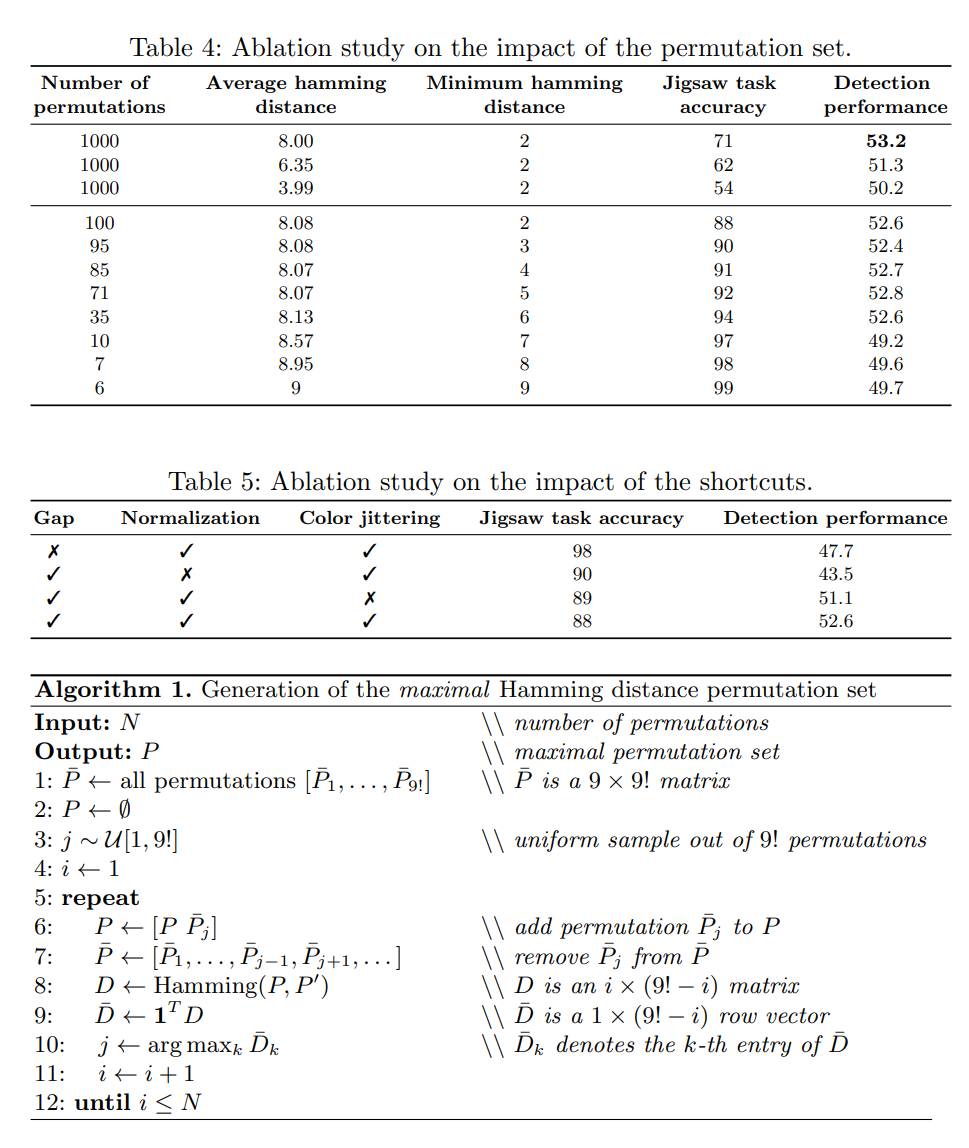
아래의 3가지 기준에 따라 여러 순열 집합을 생성하여 PASCAL VOC 2007 디텍션 작업에서 학습된 표현의 성능을 비교합니다.

1. Cardinality. 다른 순열들로 네트워크를 훈련 시키고 이것이 학습된 feature에 미치는 영향을 확인합니다.

   총 순열 수가 증가함에 따라 직소 task에 대한 학습이 점점 더 어려워 지고 디텍션 작업의 성능이 순열 수가 증가함에 따라 증가한다는 것을 발견했습니다.

2. Average Hamming distance. 우리는 1000개의 순열의 부분집합을 사용하고 해밍 거리에 따라 선택합니다. 순열 사이의 평균 해밍 거리가 직소 퍼즐의 난이도를 제어하고, 객체 탐지 성능과도 관련이 있습니다.

   이 실험에서는 해밍 거리를 최소, 평균, 최대로 나눈 3가지 선택 사항에 대해 훈련된 CFN의 물체 감지 성능을 비교합니다.

   이 테스트에서 우리는 넓은 해밍 거리가 바람직 하다는 것을 볼 수 있습니다.

3. Minimum hamming distance. 순열사이의 가능한 최소 거리를 늘리기 위해 100개의 초기 항목에서 유사한 순열을 제거합니다.

   앞에서 말한바와 같이 최소 거리는 작업을 덜 모호하게 만드는데 도움이 됩니다.

이 alblation study는 다음과 같은 최종 고려 사항을 지적하는 것 같습니다.

“A good self-supervised task is neither simple nor ambiguous.”

Preventing Shortcuts

SSL 방식에서 shortcuts는 pretext를 해결하는데 유용하지만 다른 visual task에는 유용하지 않습니다.

CFN은 직소 퍼즐을 해결하기 위해 다음과 같은 shortcuts를 사용할 수 있음을 실험적으로 보여줍니다.

• Low level statistics: 인접한 패치에는 픽셀 강도의 평균 및 표준편차와 같은 low level statistics가 포함됩니다.

  이를 막기 위해 각 패치의 평균 및 표준 편차를 독립적으로 정규화합니다.

• Edge continuity: 직소 퍼즐을 쉽게 풀기위한 방법중 하나는 경계 연속성입니다.

  85x85 픽셀에서 64x64픽셀 타일을 무작위로 선택합니다.

  이를 통해 타일 사이에 21픽셀의 간격이 생길 수 있습니다.

• Chromatic Aberration: Chromatic Aberration은 이미지 색상 채널 사이의 경계가 뚜렷할 때 자주 발생하는 현상입니다.

  이러한 왜곡은 네트워크가 타일 위치를 추정하는 데 도움이 됩니다.

  이를 해결하기 위해 세 가지 방법을 사용합니다.

  1. 원본 이미지의 가운데를 잘라서 255x255로 resize 합니다.
  2. RGB와 Grayscale 이미지를 3:7로 학습했다.
  3. 각 타일의 픽셀에 무작위로 0,1,2를 더하거나 빼는 color jittering을 했다.

CFN filter activations

최근 CNN의 작동 원리를 이해하기 위한 시각화 연구들이 많아졌습니다.

따라서 본 논문에서도 각 층의 유닛을 Detector로 생각하고 CFN의 activation을 분석합니다.

ImageNet의 검증 셋에서 1M개의 patch(무작위로 뽑은 20개의 64x64)를 추출하여 CFN의 입력으로 넣습니다.

그 후 입력에 따른 각 층의 출력을 $l1\ norm$으로 계산하여 순위를 매겨 가장 높은 16개의 패치를 선택합니다.

각 층에는 여러개의 채널이 있으므로 가장 중요한 채널을 직접 선택합니다.

아래의 그림에서 우리는 레이어당 6개의 채널(각 층의 채널은 여러개 이므로)에 대한 상위 16개 활성화 패치를 보여줍니다.

(a),(b)는 texture에 전문화 되어있고,일부 채널은 좋은 face detector도 될 수 있습니다.(c)

(d),(e)는 part detector임을 알 수 있습니다.

Image Retrieval

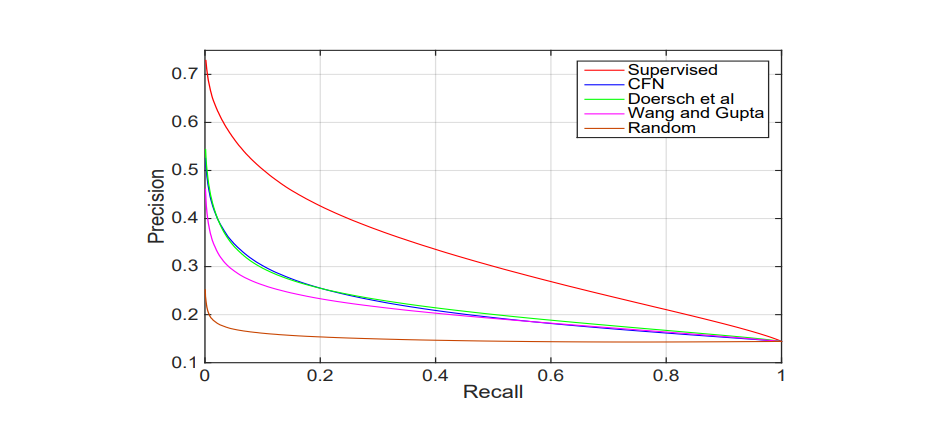
이 섹션에서는 이미지를 검색하기 위해 features를 정성적으로 정량적으로 평가합니다.

우리는 이 실험을 통해 CFN의 features가 비슷한 모양의 물체에 매우 민감하고 종종 같은 범주 내에 있음을 알 수 있습니다.(아래의 그림에서 (c))

정량적으로 평가 했을 때 위와 같은 그래프가 나옵니다.

CFN은 Doersh와 매우 비슷해 보입니다.

하지만 우리는 굉장히 단순한 metric을 사용했기 때문에 정확하진 않습니다. (위에서 봤듯이 CFN은 fine-tuning을 사용할 시에 더 좋은 성능을 보였기 때문입니다.)

Conclusion

CFN이 각각 이미지 패치를 object part로 학습하고, 각각의 part가 object에서 어떻게 재 조합 되는지(직소 퍼즐)를 학습합니다.

그렇게 학습된 CFN의 features들은 다른 visual task에서도 좋은 성능을 보였습니다.

Reference

Jigsaw Puzzle-Paper