ResNet
26 Mar 2020 | visionDeep Residual Learning for Image Recognition
Implementation
Abstract
이전까지 사용되었던 것 보다 훨씬 더 깊은 네트워크를 학습 시키기 위해 residual learning을 제시합니다.
참조되지 않은 함수를 학습하는 대신, 레이어의 input을 참조하도록 학습 하는 레이어를 명시적으로 재구성합니다.
residual network가 최적화 하기 쉽고, 깊이의 증가로부터 정확도를 얻을 수 있음을 보여주는 포괄적이며 경험적인 근거를 제시합니다.(실험적 결과)
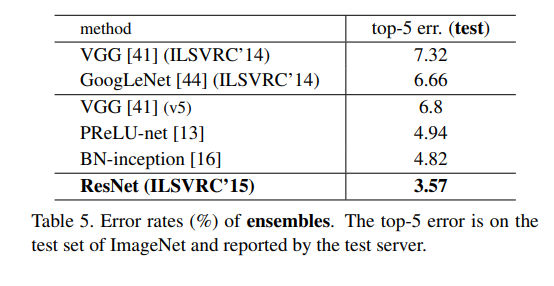
ILSVRC & COCO15등의 대회에서 모두 1등함.
Introduction
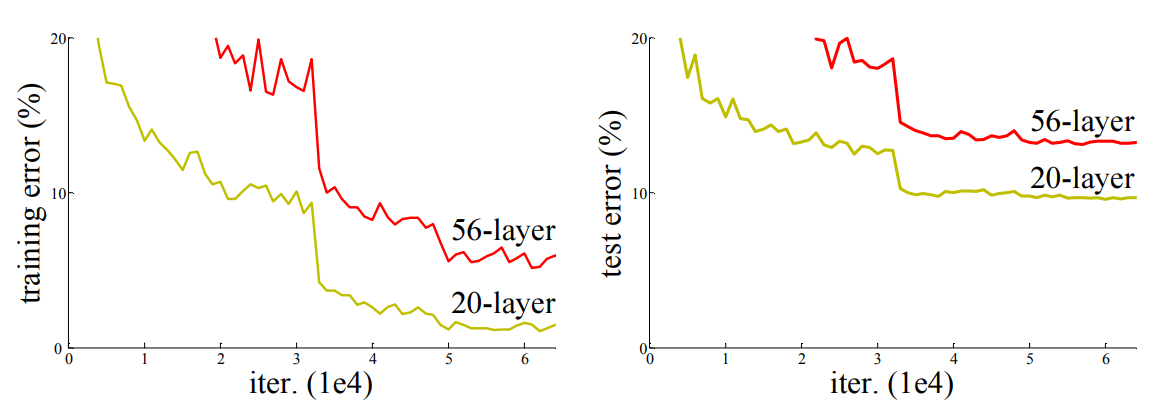
깊이를 늘리면 네트워크의 성능이 단순히 좋아질 것이라는 예측과는 달리 실제로 깊이를 무작정 늘리면 shallow architecture에 비해 deep network는 성능이 좋지 않습니다.
논문에서는 이 문제를 ‘degradation’ 때문이라고 말합니다.
Overfitting : 모델이 traininga data에 맞게 너무 잘 표현되어 반대로 val, test data에서 성능이 떨어지는 경우
degradation : training, test 모두 성능이 잘 나오지만, depth가 깊어질 수록 성능이 떨어지는 경우
하지만 shallow architecture + identity mapping으로 네트워크를 늘리면 identity의 특성상 최소한 깊이에 상관없이 shallow만큼의 성능은 보장됩니다.
위의 shallow + identity mapping 구조가 현재로서는 깊이를 늘리는(성능을 보장하면서) 최적의 구조인데, 이 방식에서 더 나은 solution이 보이지 않으므로 residual learning framework를 적용해봤습니다.
residual mapping을 최적화 하는 것이 original, unreferenced mapping을 최적화 하는 것 보다 더 쉬울 것이라는 가설을 세워 봅시다.
stack of non-linear를 identity mapping에 fit 하는 것 보다 residual을 0으로 보내는게 더 쉬울 것입니다.
사실 직관적으로 id mapping을 레이어 스택으로 학습 시켜서 따라한다는게 말이 안될 것 같습니다.
또한 기존의 방식은 추가된 레이어들로 인해 성능이 떨어진다는게 그 증거가 되겠죠?
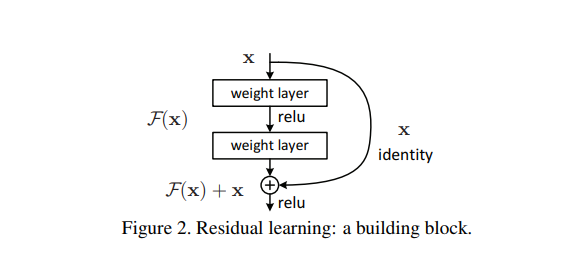
shortcut connection은 identity mapping을 단순하게 구현한 것이고, 그 output은 stacked layer의 output과 합쳐집니다.
이러한 가설에 의해 나온 구조이지만 성능이 매우 뛰어나서 모든 대회에서 1등할 수 있었습니다.
Deep Residual Learning
$\mathcal{H}(x)$를 몇 개의 stacked layer에 맞는 underlying mapping으로 생각해 봅시다.(전체 네트워크일 필요는 없습니다.)
x를 여러 non-linear layer를 거쳐 복잡한 함수 $\mathcal{H}(x)$에 점근적으로 근사가 가능하다고 가정하면, residual function $\mathcal{H}(x)-x$또한 근사할 수 있습니다.
$\mathcal{F}(x) := \mathcal{H}(x)$ 와 $\mathcal{F}(x) := \mathcal{H}(x) - x$ 의 차이를 말하는 것 같습니다.
$x -> \mathcal{H}(x)$이 가능하다면 $\mathcal{H}(x) - x$를 0으로 만드는 것도 가능하지 않을까요?
Degradation 문제는 solver가 multiple nonlinear layers에 의해 identity mapping에 근사하는게 어렵다는 것을 보여줍니다.
실제로는 identity mapping이 최적은 아닙니다, 하지만 우리가 재정의한 식은 문제를 사전 조정하는데 도움이 될 것 입니다.
만약 최적화 함수(이상적인 경우)가 zero보다 identity mapping에 가깝다면, 기존 방식처럼 0에서 찾는 것 보다 identity mapping을 기준으로 찾는 것이 훨씬 더 쉬울 것입니다.
Identity Mapping by Shortcuts
만약 input과 output의 차원이 다르면 (2)의 수식을 사용해서 차원을 맞춰 줍니다.
$\mathcal{F}$ 가 하나의 층만 가진다면 Residual learning의 이점이 사라지므로 두 개 이상의 층을 가져야 합니다.
Network Architecture
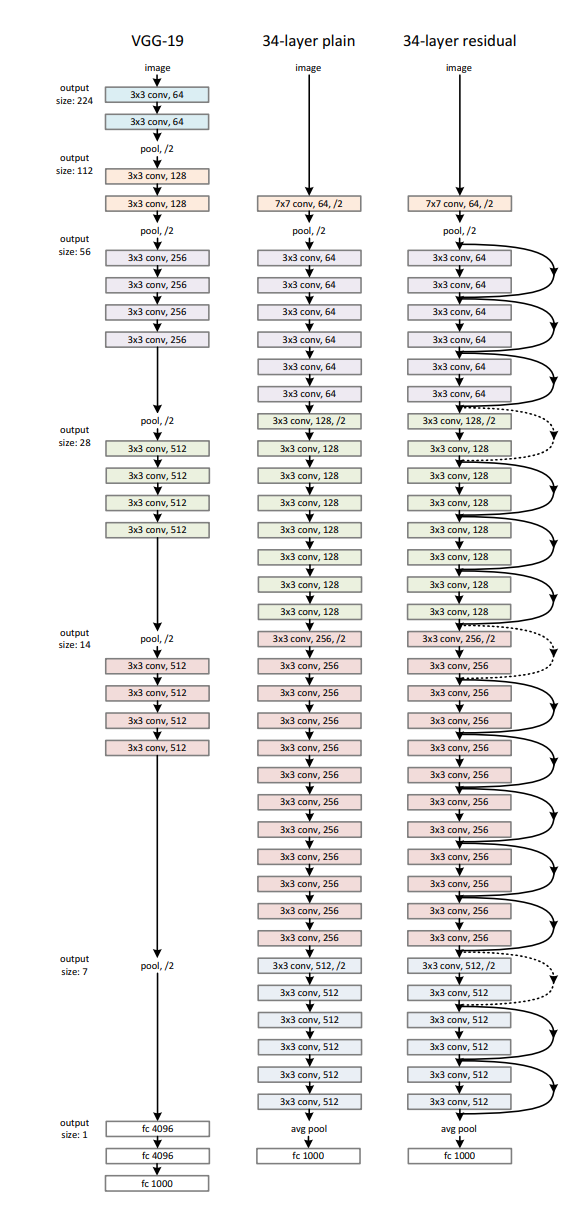
Plain Network의 경우 VGG에서 영감을 받았습니다.
필터는 모두 3x3 크기를 가지며, 두 가지 간단한 디자인 규칙을 따릅니다.
- 동일한 feature map size의 경우 레이어는 필터 수가 동일합니다.
- feature map size를 절반으로 줄이면, 레이어 당 시간 복잡성을 유지하기 위해 필터 수가 두배가 됩니다.
Plain Network는 VGG보다 필터가 적고 복잡도가 낮습니다.
GAP를 이용해 Fully connected를 줄인게 효과가 굉장히 클 것 같습니다.
GAP : 기존의 FC를 대체하여 feature map에 대해 평균을 취하고 이를 직접 softmax layer에 연결 시키는 방식
Residual Network는 위의 Plain Network를 기반으로 해서 shortcut connections를 삽입합니다.
input과 output의 차원이 같은경우 위 (1)식을 그대로 적용 할 수 있고,
점선의 경우 차원이 바뀌므로 2가지 옵션을 취합니다.
(A)증가된 차원만큼 zero padding
(B)Eqn.(2)를 사용하여 Projection(done by 1x1 conv)
Implementation
ImageNet 데이터에 대한 구현은 AlexNet과 VGGNet을 따릅니다.
BatchNormalization을 사용하며 Dropout은 사용하지 않고, He 를 사용하여 weigth initialization을 수행합니다.
batchsize = 256로 하며 SGD를 사용하여 학습합니다.(lr = 0.1, momentum = 0.9, weight decay = 0.0001)
Experiments
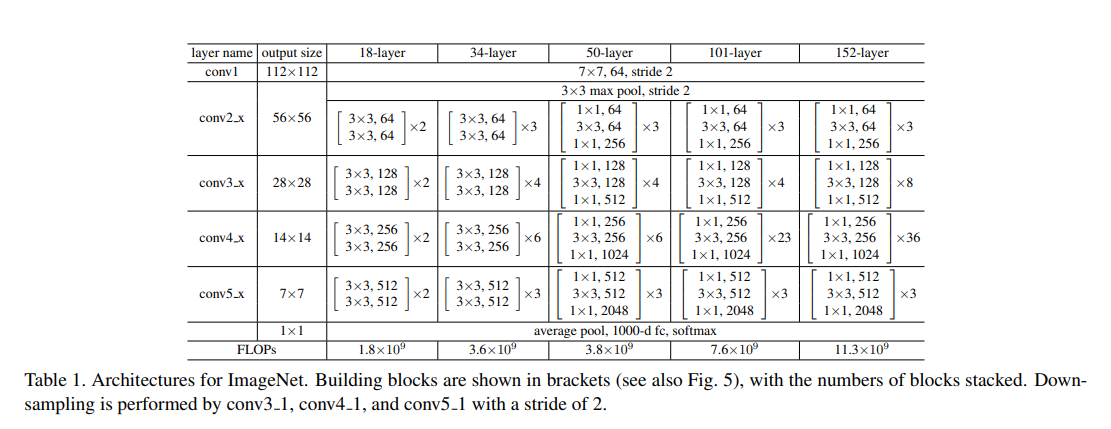
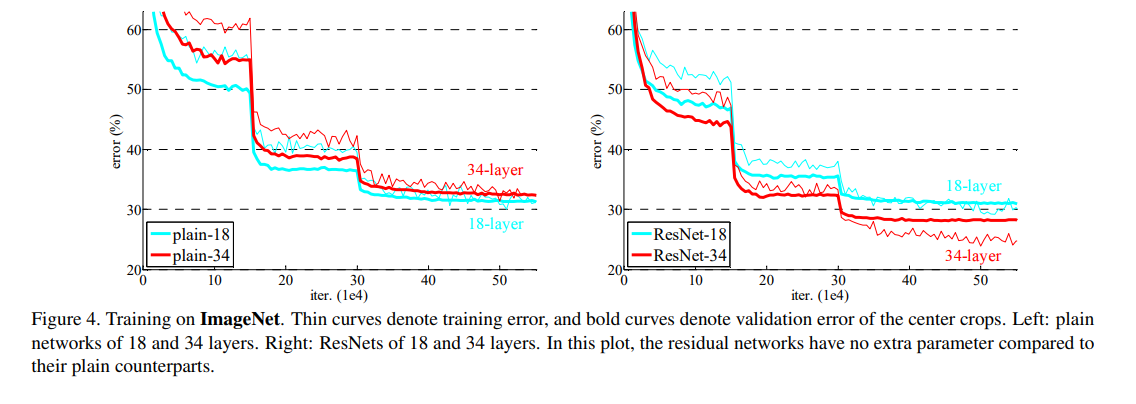
Plain Network. 우선 18-layer와 34-layer plain nets를 평가합니다.
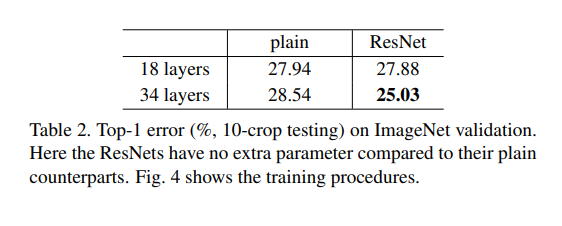
Table.2 를 보면 알 수 있듯, 34-layer에서 더 높은 validation error가 나타납니다.
우리는 이러한 최적화의 어려움이 Vanishing gradients때문에 발생한다고 생각하지 않습니다.
우리는 네트워크 구조에서 BN을 사용했고 foward propagation과 backward에서 신호를 모두 검사했습니다.
사실 Plain-34도 Table.3 를 보면 나쁜 성능은 아닙니다.
우리는 Deep Plain Network가 기하 급수적으로 낮은 수렴률을 가질 수 있으며 이는 training error의 감소에 영향을 미친다고 추측합니다.
이러한 최적화가 어려운 이유는 앞으로 연구 될 것입니다.
Residual Network. 우리는 resnet-18과 resnet-34에 대해서 평가합니다.
baseline은 Plain nets와 동일하고 shortcut connection이 필터에 추가됩니다.
우리는 옵션 (A)의 shortcut connection을 사용합니다.
(A) : identity shortcut (General case)
but 차원이 맞지 않을 경우 Zero padding 해준다.
Table.2와 Fig.4의 오른쪽을보면 Plain과 상황이 역전된 것을 볼 수 있습니다.
34-layer의 resnet-34가 resnet-18보다 훨씬 더 성능이 좋음을 볼 수 있고,
더 중요한 점은 resnet-34가 상당히 낮은 training error와 함께 validation data로 일반화가 가능하다는 점입니다.
이것은 Degradation문제가 해결됐으며, 깊이의 증가로 인한 정확도 향상을 얻을 수 있음을 뜻합니다.
또한 Plain nets와 비교해서도 Table.2를 보면 resnet-34가 Plain-34보다 더 좋은 성능을 내는 것을 볼 수 있습니다.
마지막으로 18-Plain/Resnet을 비교해 보면 성능은 차이가 없어보이지만 Fig.4를 보면 18-resnet이 훨씬 더 빨리 수렴하는 것을 볼 수 있습니다.
Identity vs Projection Shortcuts
우리는 지금까지 parameter-free인 identity mapping이 학습에 도움이 된다는 것을 보여주었습니다.
이제 우리는 Projection shortcuts(Eqn.(2))에 대해 알아봅시다.
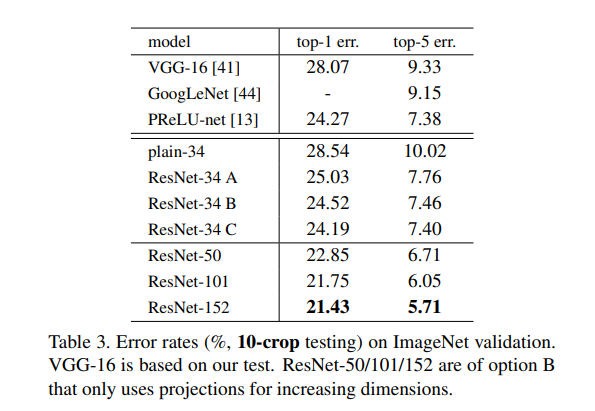
Table.3를 보면 3가지 옵션을 비교했습니다.
(A) : Zero padding(parameter-free)
(B) : Projection shortcuts(used for increasing dimension) 나머지 경우엔 (A)
(C) : All shortcuts are projection
성능은 직관적으로나 실험 결과로보나 (C)>(B)>(A)입니다.
사실 학습만 할 수 있다면(컴퓨팅 리소스가 남으면) (B),(C)는 파라미터를 추가하게 되므로 성능이 더 잘 나올 것 입니다.
(B)가 (A)보다 나은 이유는 A의 0으로 채워진 차원에 실제로 residual learning이 없기 때문입니다.
또한 (C)가 (B)보다 나은 이유는 많은 Projection shortcuts에 의해 도입된 파라미터 때문입니다.
그러나 (A),(B),(C)의 작은 차이점은 Degradation문제를 해결하는 데 projection shortcuts가 필수적이지 않음을 나타냅니다.
그래서 우리는 논문의 나머지 부분에서는 (C)를 사용하지 않으므로 메모리와 시간복잡성 그리고 모델의 크기를 줄입니다.
Deep Bottleneck Architecture
우리는 training time에 대한 여유로 인해 block을 bottleneck design으로 수정합니다.
각 residual function $\mathcal{F}$에 대해 2개 대신 3개의 레이어 스택을 사용합니다.
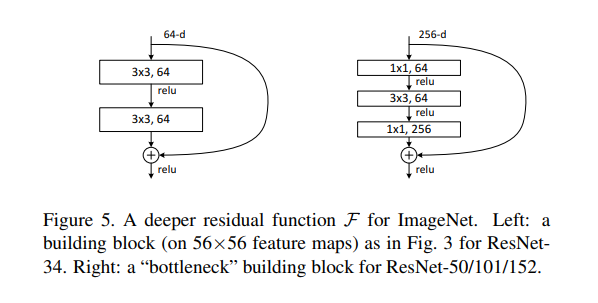
3개의 레이어는 각각 1x1 , 3x3, 1x1이며, 1x1은 차원을 감소시키거나 증가(복원)시키는 역할을 합니다.
3x3 레이어에는 더 작은 input/output 차원을 남겨둡니다.
Fig.5를 보면 두 설계가 비슷한 시간 복잡도를 가짐
레이어의 input이 256-dimension이므로 shortcut connection과 더해주려면 차원을 맞춰야 하기 때문에
계산상의 이점을 위한 (차원축소) - convolution - shortcut과의 연산(차원복원) 구조를 띄게 됩니다.
parameter-free identity shortcuts는 특히 bottleneck architecture에서 중요합니다.
만약 identity shortcuts이 projection으로 대체되면,
shortcut이 두개의 고차원에 연결되어 있기 때문에 시간 복잡도와 모델의 크기가 두 배로 증가함을 알 수 있습니다.
따라서 identity shortcuts는 bottleneck design에서 더 효율적인 모델로 이어집니다.
Exploring Over 1000 layers.
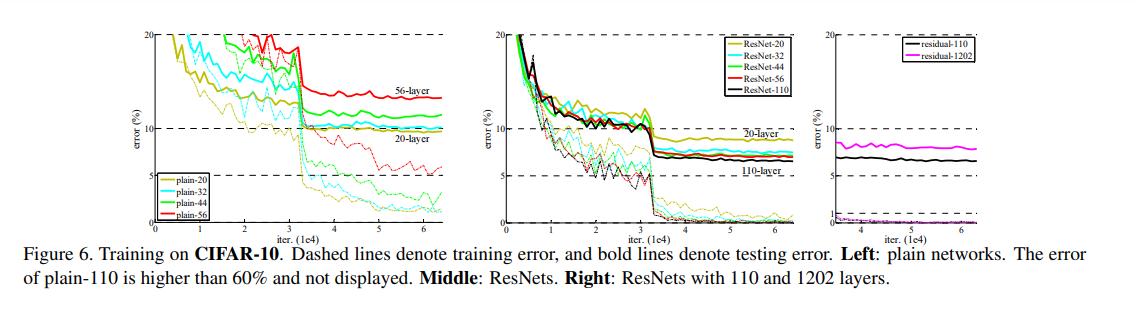
재밌는 사실은 제일 오른쪽 그래프입니다.
Residual learning을 써도 레이어가 1000개이상 쌓이면 다시 training error가 더 높아지는 현상이 발생합니다.
논문의 저자는 이 문제는 degradation이 아닌 Overfitting 때문이라고 합니다.
위 그래프는 Cifar-10 dataset인데, 레이어가 1000개가까이 쌓이면 불필요하게 모델의 사이즈가 너무 커지고, Cifar-10같은 작은 데이터 셋으로 이 모델을 학습시키기는 너무 어렵기 때문입니다.
저자들은 Cifar-10 데이터를 사용해서 Overfitting이라고 정의했지만,
저는 Resnet이 기존에 40~60 layer에서 발생하던 degradation 문제를 100-layer level로 넘겼다고 생각합니다.
1000-layer짜리를 만족시킬 만한 training data로 resnet-1212학습이 가능할지, 과연 Overfitting일지 degradation 문제 일지 궁금합니다.(나중에 엄청 좋은 컴퓨터 생기면 해보는걸로..!)

Comments