Yolo
19 Feb 2020 | detectionYou Only Look Once: Unified, Real-Time Object Detection
이름부터 매력적인 Yolo모델입니다.
저자분은 자신의 모델이 군사적인 목적으로 사용되는 것을 보고 충격을 받아 CV research를 그만 두신 것으로 알고, Yolo v4 부터는 다른 팀에서 만든 것으로 알고 있습니다.
R-CNN계열과의 차이점은 속도에 있습니다. 이름에서 알 수 있듯 한번 보고 바로 추론을 해내는 모델입니다. 속도(Real-Time)를 얻은 대신 정확도는 조금 포기했습니다. 어떻게 빠른 속도를 얻을 수 있었는지 알아봅시다.
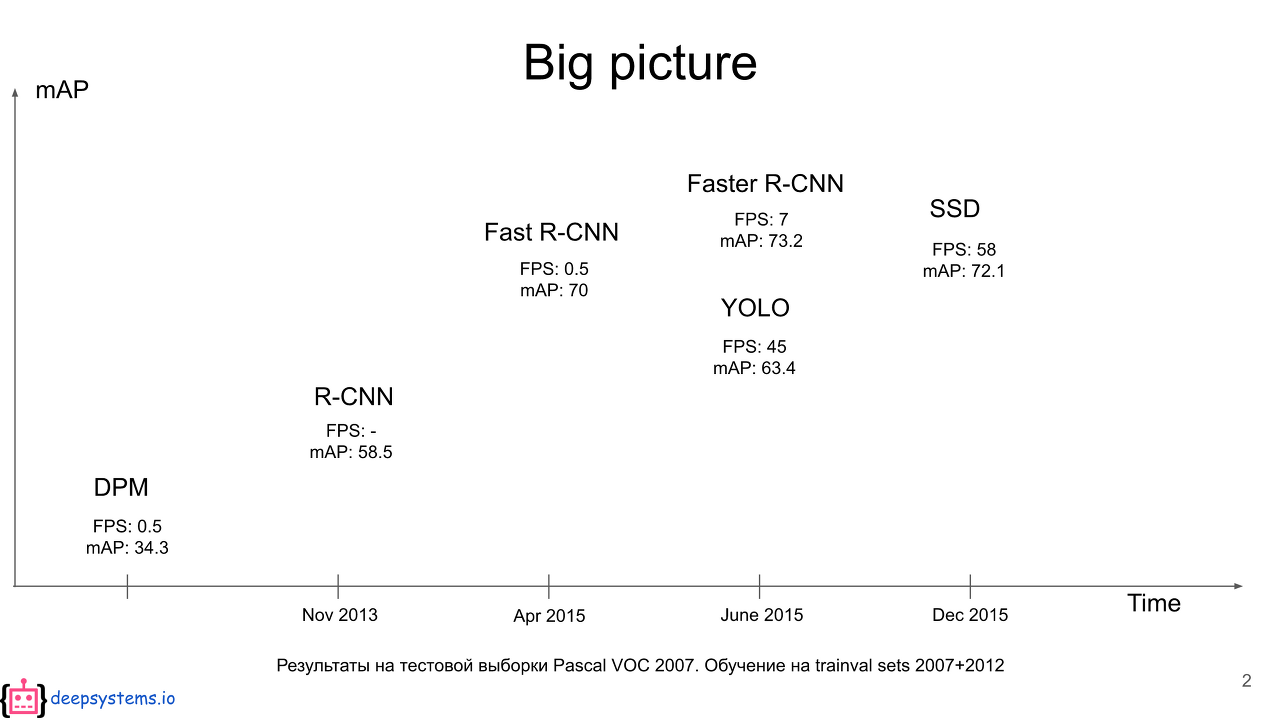
Introduction
타이틀에서 알 수 있듯 욜로의 핵심은 Unified를 통한 Real-Time Detection입니다.
기존의 Detection 모델은 Region proposals - Classification 이라는 two stage 구조를 갖습니다.
이런 two-stage 구조는 정확도 측면에선 좋겠지만 속도 측면에선 매우 느릴 수 밖에 없는 구조입니다. 욜로는 이 구조를 single regression문제로 재구성합니다. 이를 위해서 욜로는 Single Network로 구성됩니다.
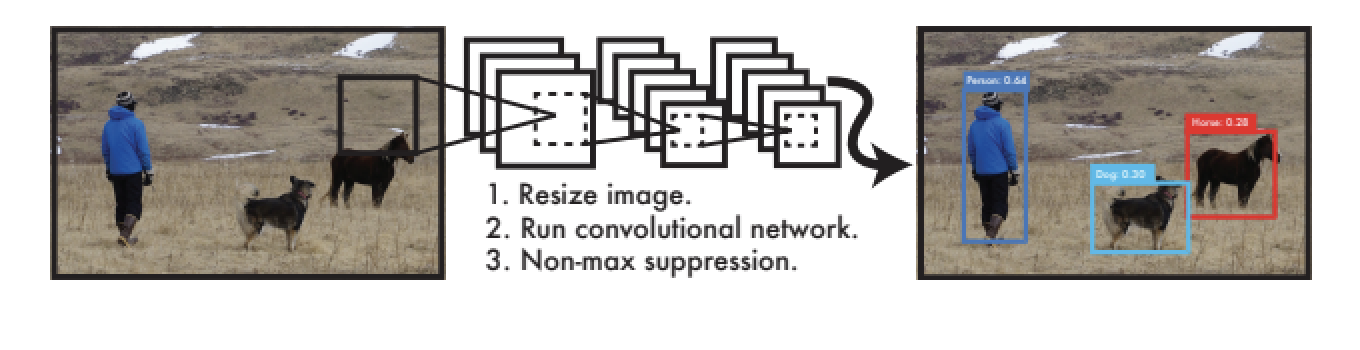
Unified Detection
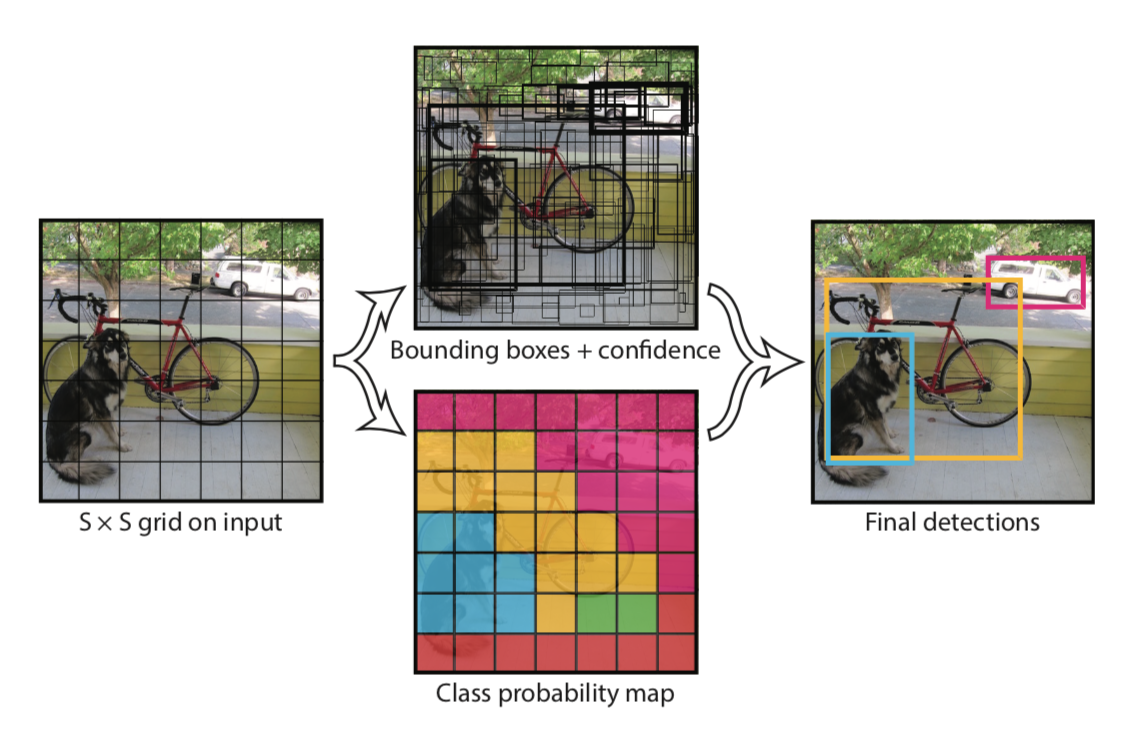
- R-CNN과 다르게 전체 이미지를 사용하여 SxS 그리드로 나눕니다.
- 각 셀에 $(x,y,w,h,c)$를 B(num of box)개 예측합니다.
- 여기서 confidence scroe $c$는 $Pr(object) \times IOU$로 구합니다.
- 각각의 셀은 클래스에 대한 예측값들을 갖게 됩니다. $Pr(Class_i\vert Obejct)$ 기존과 달리 배경은 클래스에 넣지 않습니다.
Architecture
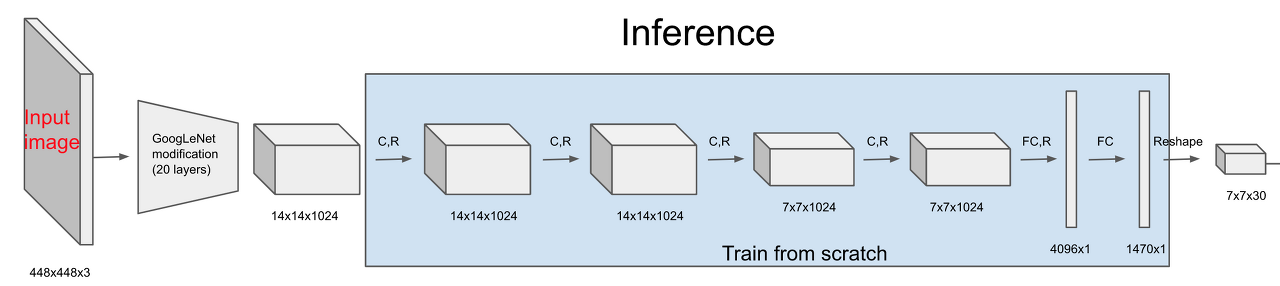
저자는 구글넷에서 영감을 받아 ImageNet으로 pretrain된 구글넷의 변형을 사용합니다. 앞의 20개의 레이어는 거의 구글넷과 유사하며, 뒤의 4개의 conv 레이어를 Detection에 맞게 학습시킵니다.
마지막 7x7x30에 집중해봅시다. Output tensor는 $S\times S\times (B\times 5 + C)$ 로 정의됩니다. 우리의 출력 값은 클래스의 확률과 bounding box 좌표에 대한 확률입니다.(Pascal VOC를 사용해서 S=7, B=2, C=20)
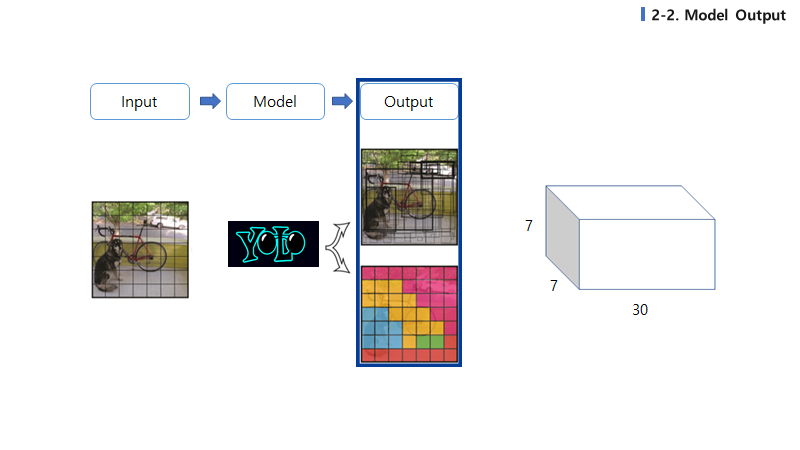
B = 박스의 개수 5 = $(x,y,w,h,c)$ 이므로 앞의 10차원은 박스에 대한 정보이고, 그 뒤의 20차원은 클래스에 대한 확률입니다.
좀 직관적으로 설명하자면 1x30차원 벡터에서 앞의 5차원은 box1에 대한 정보, 뒤의 5차원은 box2에 대한 정보입니다.
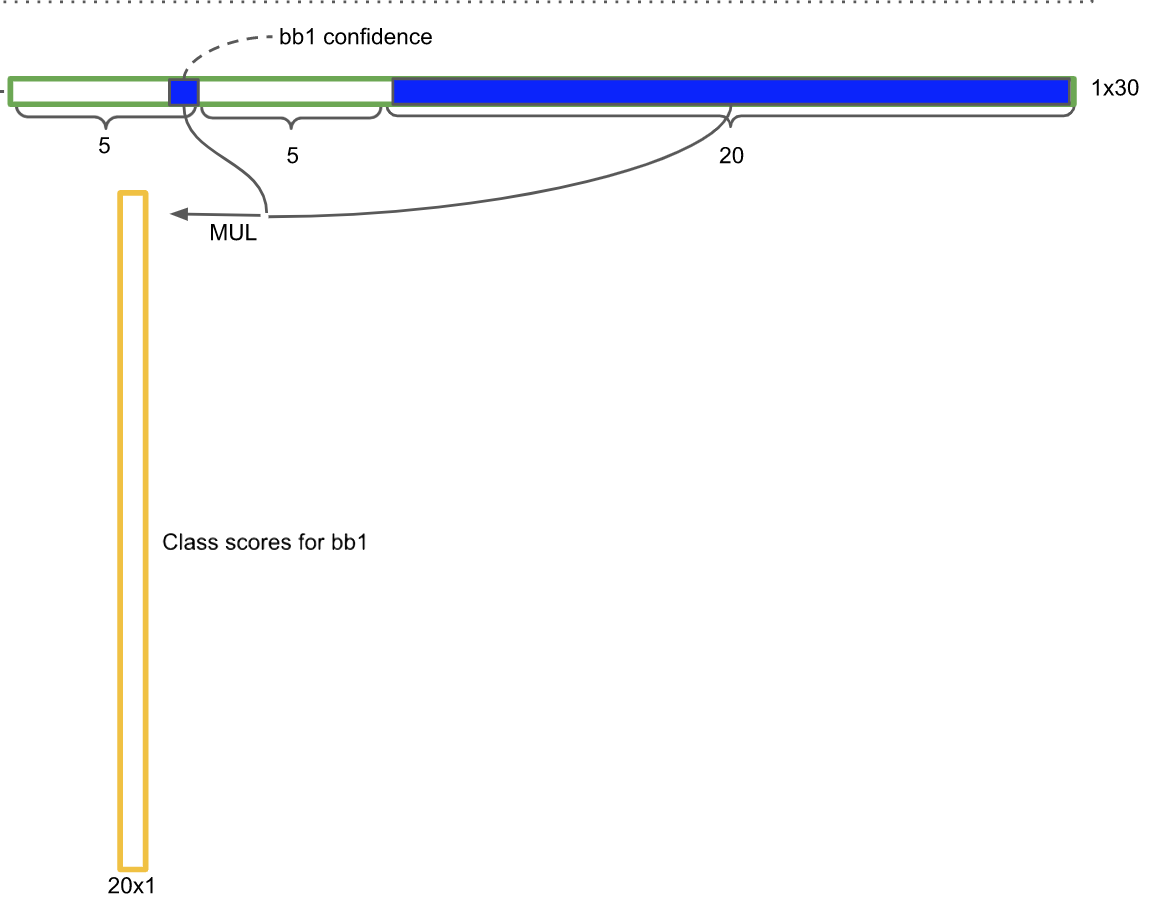
이전에 우리는 박스의 신뢰도를 $Pr(object)\times IOU$ 각 셀별 클래스의 확률을 $Pr(Class_i\vert Obejct)$로 구했습니다. 두 값을 곱해주면 $Pr(Class_i)\times IOU$가 되고 각 박스가 해당 클래스일 확률을 나타냅니다.
그런데 잠시만요, 저희는 각 셀에 대해 bounding box를 두 개씩 생성해서 위 예시에선 총 98개가 생성됩니다. 만약 각 객체에 중복된 박스가 생기면 어쩌죠?
여기서도 R-CNN처럼 NMS를 사용합니다.

클래스가 dog인 경우에 대해 98개의 Box의 확률을 정렬해서 나타내고 확률 값이 max인 케이스와 그보다 작은 케이스에 대해 IOU를 계산합니다. 만약 IOU가 0.5보다 크면 두 박스는 같은 객체를 포함할 확률이 높으므로 작은 박스를 0으로 바꿉니다.
한 루프를 돌고 나면 그 다음 가장 큰 확률에 대해 똑같은 연산을 수행합니다.
이 과정이 사실 왜 필요한지는 잘 모르겠습니다.
그냥 제일 확률이 높은 값을 박스로 생각하고 나머지를 다 밀어버리면 될 것 같은데…
이런 과정을 거치고 나면 각 클래스에서 2 가지 케이스(최초의 max값, 그 max값과의 IOU threshold를 넘지 못해서 0이 되지 않은 값)이 남습니다.
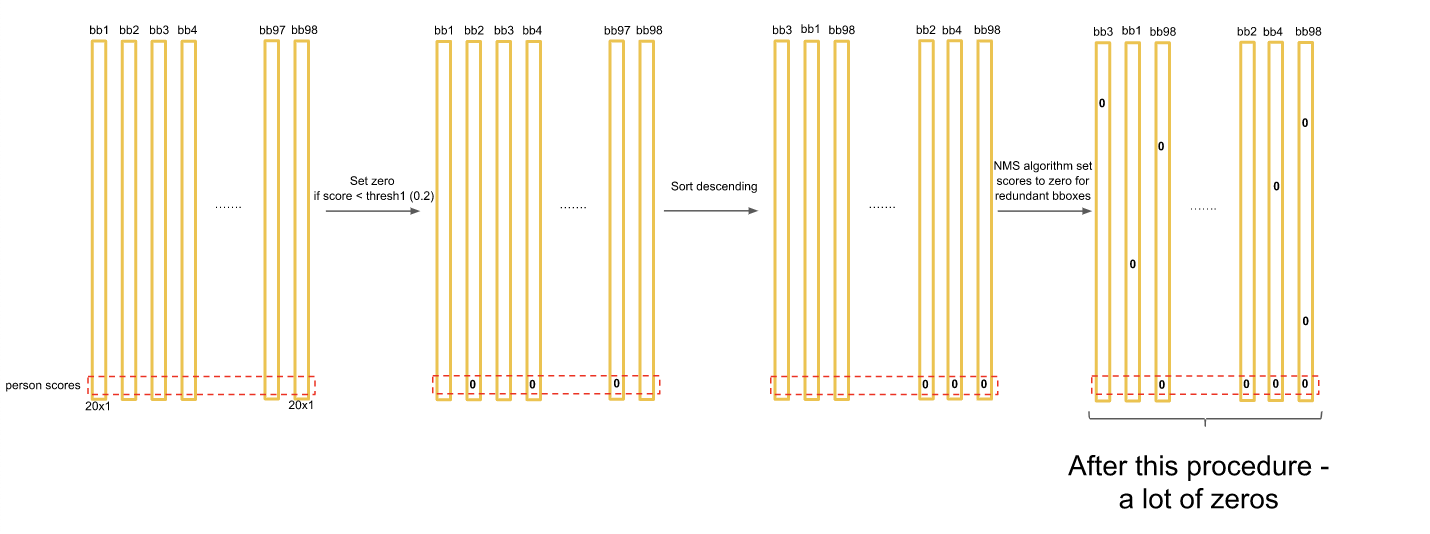
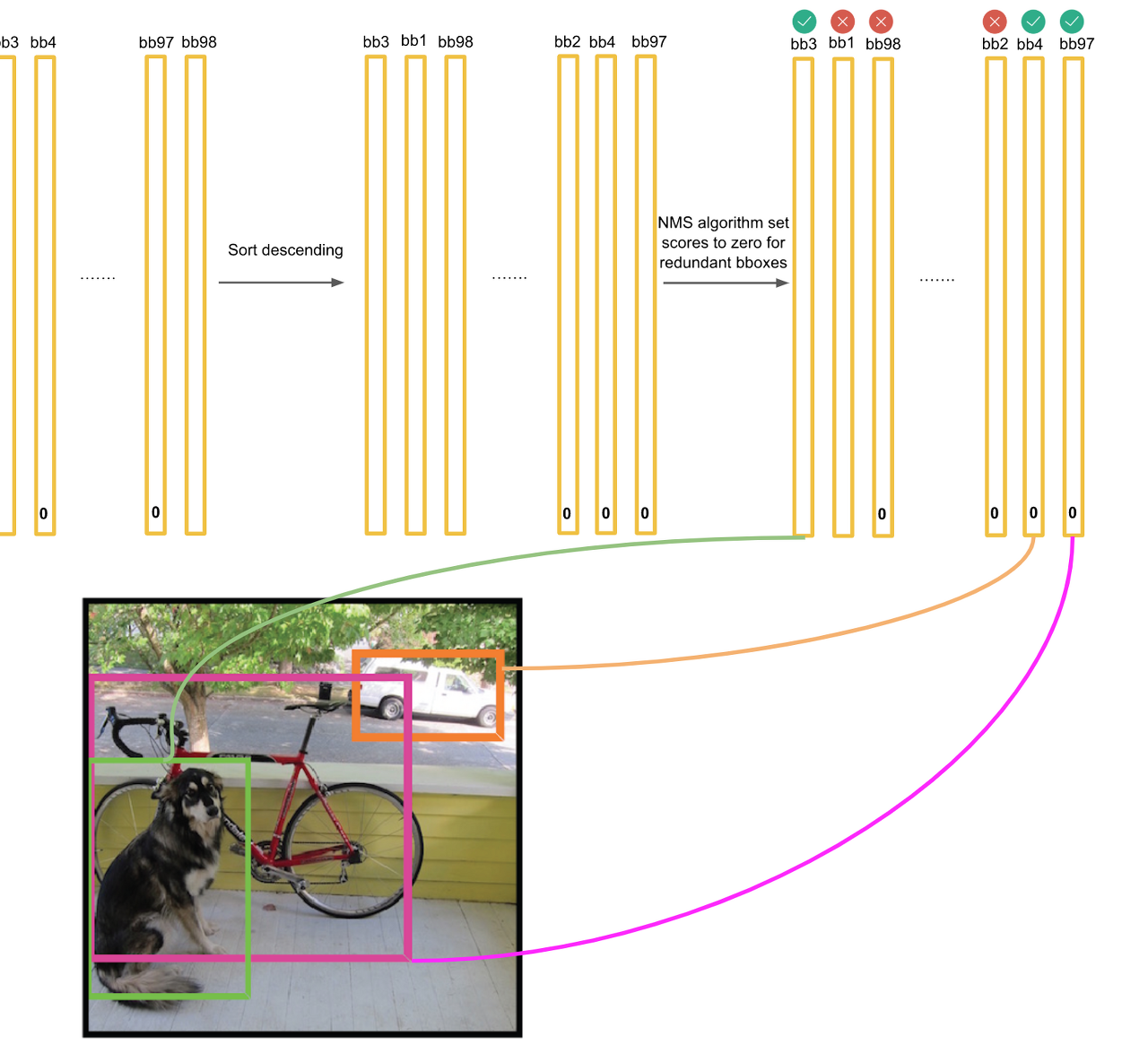
대부분의 값이 0으로 바뀝니다. 그리고 각 박스별로 가장 높은 스코어의 클래스를 가지고와서 그 클래스에 맞는 색으로 박스를 그립니다.(만약 max score가 0이면 그 박스는 그리지 않고 넘어갑니다.)
Loss Function
복잡해 보이지만 간단합니다.
- 객체가 존재하는 grid cell i의 j번 째 b-box의 (x,y)에 대한 loss
- 객체가 존재하는 grid cell i의 j번 째 b-box의 (w,h)에 대한 loss
- 객체가 존재하는 grid cell i의 j번 째 b-box의 Confidence score에 대한 loss
- 객체가 존재하지 않는 grid cell i의 j번 째 b-box의 Confidence score에 대한 loss
- 객체가 존재하는 grid cell i의 조건부 클래스 확률에 대한 loss
$\lambda_{coord},\lambda_{noobj}$가 나오는데 각각의 의미는 다음과 같습니다.
모든 이미지에서 대부분의 셀은 백그라운드입니다. 해당 셀의 신뢰도가 ‘0’으로 채워지면 객체를 포함하는 셀의 그래디언트를 압도하여 모델이 불안정해지고 이는 학습 조기종료의 원인이 됩니다.
이를 해결하기 위해 박스 예측으로 인한 손실을 늘리고, 객체가 포함되지 않는 박스에 대한 신뢰도 예측으로 인한 손실을 줄입니다. 이를 위해 $\lambda_{noobj}$를 사용합니다.
이 파라미터가 욜로가 백그라운드에 강하도록 만들어 줍니다.
대부분의 이미지는 객체가 포함되지 않은 부분(배경)이 많고, 저런 과정을 거치지 않을 경우 배경을 객체로 인식하게 된다고 합니다.
$\lambda_{coord}$는 박스의 좌표에 대한 loss를 더 크게 잡기 위해서 논문에서는 5로 설정합니다.
Conclusion
전반적으로 어려운 내용이지만, 센세이션합니다. (어떻게 저런 생각을 했지…)
저자는 대학원생 때 저런 논문을 쓴 것으로 아는데 제가 대학원에 진학하면 저런 논문을 쓸 수 있을까 싶습니다.
마지막으로 욜로의 단점만 짚어보고 마무리 하겠습니다.
욜로는 박스를 여러개로 예측하지만, 하나의 클래스만 예측하기 때문에 박스 예측에 강력한 ‘공간적 제약’을 부과합니다.
여기서 ‘공간적 제약’이란 모델이 예측할 수 있는 주변 수를 제한하는 것으로 예를 들어 조류 무리등의 그룹을 예측하기 어렵다는 것입니다.(그리드 단위로 예측하니까요!) 또한 모델이 데이터로 부터 박스 예측을 학습하기 때문에 새롭거나 특이한 종횡비로 구성된 객체를 일반화 하는데 어려움을 겪습니다.(이를 Localization error 라고 합니다.)
그리드 단위로 예측하기 때문에 객체가 겹쳐있는 경우 예측이 제대로 되지 않는다고 합니다.
또한 작은 박스의 경우 로스 함수에서 볼 수 있듯 IOU에 더 민감하게 영향을 줘서 localization이 다소 부정확합니다.(Fully connected를 두 번 거치면서 좌표값을 예측하지만 이는 맞추기 힘들다고 합니다.)
하지만 반대로 말하면 저런 점을 제외하면 모두 장점입니다.
- 빠른 속도
- 심지어 성능도 좋음
- 백그라운드에 강함
- 일반화에 강함


Comments