Batch Normalization
11 Feb 2020 | techBatch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
논문의 저자들은 기본적으로 딥러닝 학습이 어려운 이유를 이전 레이어가 가진 파라미터가 변화하고 이로 인한 레이어의 입력 분포가 변경되기 때문이라고 주장합니다.
논문에선 이를 ‘Internal Covariance Shift’ 라고 말하는데요, 그럼 어떻게 해결할 수 있을까요?
Whitening
가장 단순한 방법은 레이어의 입력 분포를 정규화 하는 것입니다.
만능키인 정규분포를 통해 정규화 해봅시다. ~$N(0,1)$ 그런데 한 가지 재밌는 사실이 있습니다.
정규분포화 하려면 z-score normalization하겠다는 소리인데 이 연산에는 기댓값을 빼주는 부분이 있습니다.
\[Z = \frac{x-\mu}{\sigma}\]일반적인 딥러닝의 연산 방식을 생각해 봅시다. bias를 더 해주는 연산 부분에서 기댓값과 맞물려 문제가 발생합니다.
편의상 피드포워드 연산을 다음과 같이 가정하겠습니다.
\[1.\: y=u+b \\ 2.\: \hat y = y-E[y]\]입력 데이터가 $u$, bias가 $b$ 일 때 이 연산을 마치고 나온 $y=u+b$ 에 대하여 경사 하강법을 적용하면 $b=b+\triangle b$가 되겠죠? 이제 다시 피드포워드 연산을 수행해봅시다.
\[u+(b+\triangle b) - E[u+(b+\triangle b)] = y-E[y]\]어라? 뭔가 이상합니다. 분명 한번 업데이트를 거쳤는데 첫 번째 피드포워드 연산과 다를게 없습니다.
이 뜻은 gradient가 정규화와 파라미터에 대한 의존성을 고려하고 있지 않다는 뜻입니다.
기댓값의 성질로 인해 업데이트 되야하는 $\triangle b$가 날아가버리고 이는 Loss가 일정하게 유지된다는 뜻입니다.거기다가 이러한 방식은 공분산을 구해야 하는데 여기서 연산량이 매우 비쌉니다.
또한 추가적으로 입력 분포가 mean 0, var 1로 고정되면 activation function의 nonlinearity가 줄어 들 수 있습니다.(sigmoid에 0주변 값만 들어간다고 생각해보면…OMG)
그럼 어떻게 레이어의 입력 분포를 일정하게 만들 수 있을까요?
Mini-Batch Statistics
앞서 설명한 Whitening 방식은 단점이 너무 많을 뿐더러 모든 곳에서 미분 가능하지도 않습니다.
논문에서는 이를 해결하기 위해 두 가지 가정을 세웁니다.
- 레이어의 인풋과 아웃풋을 차원별로 독립적으로 정규화합니다.
차원별로 독립적인 정규화를 수행하려는 의미가 뭘까요?
$ X^=Cov(X)^{−1/2}X,$
$Cov(X)=E[(X−E[X])(X−E[X])⊤]$
위에서 말한 연산량이 비싸다는 이유가 위 식입니다.(invers sqaure root가 들어감)
공분산을 고려해야된다는 것은 데이터가 독립적이지 않다는 얘기입니다. 그런데 저희의 가정처럼 독립으로 생각하면 단순하게 정규화가 가능합니다.
또한 위해서 말했듯이 nonlinearity가 줄어드는 것은 네트워크의 Representation을 강제하는 것이므로 필요하지 않을 때가 존재합니다. 그러므로 identity transform이 가능하도록 만들어야 합니다.
이를 위해 정규화된 값 $\hat x$에 대해 shift, scale를 위한 파라미터 두 가지를 추가합니다.
\[y^{(k)} = \gamma^{(k)}\hat x^{(k)} + \beta^{(k)}\]이 파라미터는 기존 모델의 파라미터와 함께 학습 가능하며 네트워크의 representation을 복원할 수 있습니다.
위 식의 장점은 $\gamma=1, \beta=0$일 때 기존의 네트워크 representation이 복원 가능하고, 또한 베타가 bias처럼 행동하는데, 기존의 whitening과 달리 업데이트해도 사라지지 않습니다.
또한, activation 값을 적당히 유지하기 때문에 vanishing 현상을 막을 수 있습니다.
- Mini-batch를 이용해 activation의 mean과 var를 계산합니다.
아래 식에서 $k$는 mini-batch의 각 차원을 나타냅니다.
\[\gamma^{(k)} = \sqrt{var[x^{(k)}]} \\ \beta^{(k)}= E[x^{(k)}]\]위 식에서 summation은 모두 각 차원별로 수행됩니다.
학습 시에는 mini-batch의 mean, var로 정규화하고, 테스트 시에는 계산 해놓은 파라미터들의 평균을 이용하여 정규화 합니다.
재밌는 사실은 BN의 파라미터가 learnable이기 때문에 기존의 정규화를 거친 $\hat x$ 를 인풋으로 하는 sub-network로도 불립니다.
$\hat x^{(k)}$ 끼리 joint distribution이 학습 과정에서 변경되더라도 개별 $\hat x^{(k)}$의 mean, var유지 되므로 $y^{(k)} = \gamma^{(k)}\hat x^{(k)} + \beta^{(k)}$를 수행하는 sub-network의 효율을 개선하고 결과적으로 전체 네트워크의 학습을 개선할 것 입니다.
또한, 위 linear transform 연산을 통해 단순 정규화된 $\hat x$가 네트워크를 최적화 하는 방향으로 변화할 것 이고, 파라미터가 learnable하므로 이전에 설명한 것 처럼 단순한 whitening방식에서 볼 수 있던 경사 하강법에서 편향이 사라져 버리는 문제를 방지할 수 있습니다.
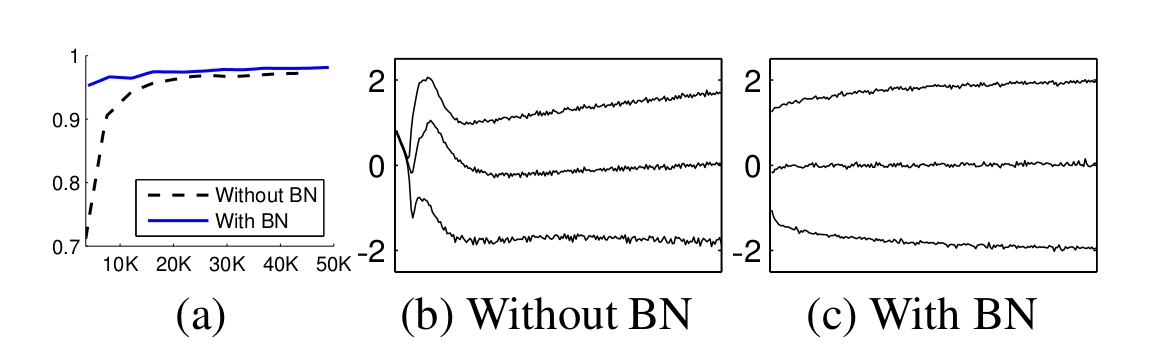
논문에서는 꼭 BN을 activation 이전에 해야 한다고 주장합니다. 이유는 다음과 같습니다.
- 인풋은 이전 단계의 activation 결과 이므로 트레이닝 과정에서 분포가 계속 변한다, 그러므로 정규화가 Covariate Shift를 없애주지 못한다.
- $Wu+b$는 좀 더 Symmetric, Non-sparse하기 때문에(가우시안 분포에 가까움) 정규화가 더 효과가 있다.
BN의 원리와 동작 방식을 살펴봤습니다. 그렇다면 BN을 사용했을 때 어떤 효과가 있을까요?
Effect
- 입력 분포가 일정하므로 높은 learning rate를 사용하여 더 빠르게 학습할 수 있습니다.
- 어떻게 보면 입력 분포를 통해 activation을 규제하는 것으로도 볼 수 있습니다. 그로 인해 dropout의 의존성을 낮출 수 있습니다.
- BN을 사용하기만 해도 정확도가 올라갑니다.
- weight initialization에 덜 민감합니다.
- regularization 효과가 생긴다고 합니다.
여기서 ‘규제’ 의 효과가 재밌는데 여러가지 방면으로 생각해볼 수 있습니다.
- 해당 레이어가 트레이닝 데이터 셋에 대해 bias 되어 있어서 그 bias를 낮춰줄 수 있으므로 규제효과를 준다.
- 학습 시에 정규화에 사용하는 mean, var이 배치 안의 샘플이 어떻게 배치되는 가에 따라 크게 달라진다. 따라서 drop out과 같이 랜덤 노이즈를 추가해주고 곱해주는 형태로 추정 가능하다.
- 즉 이런 이유로 약간의 확률적 흐트러짐(Stochastic Jittering)으로 표현할 수 있다.

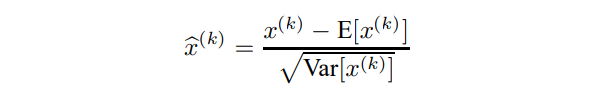

Comments