Variational AutoEncoder
28 Nov 2019 | autoenconderVariational AutoEncoder
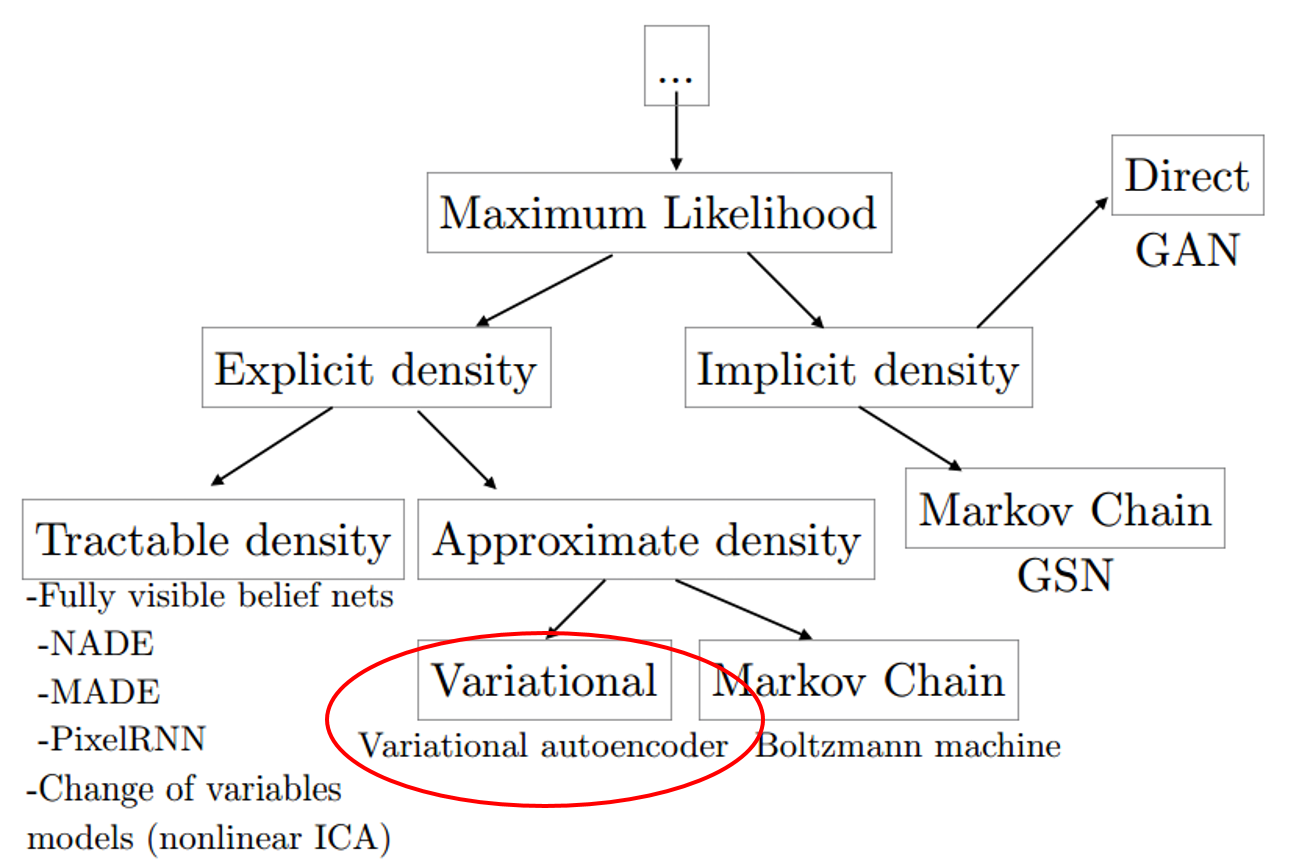
MAP에서 우리는 Prior Knowledge를 이용하여 parameter $\hat{θ}$를 추정했습니다.
그런데 현실에서는 Lack of Prior Knowledge 때문에
$p(D)$를 구하기 어렵습니다.
이러한 문제는 Generative model에 그대로 적용됩니다.
우리가 관측하는 Sample data x가 어떤 관측되지 않은 (우리가 알 수 없는) latent variable z가 영향을 미치는 어떤 random process로 부터 생성된다고 가정해 보겠습니다.

Posterior $p_θ(z|x)=p_θ(x|z)p_θ(z)/p_θ(x)$를 알고 싶은데 이를 계산하기위해서 필요한 $p_θ(x) = \int_z p_θ(x|z)p_θ(z)dz$가 계산이 불가능한(intractable)경우가 많기 때문입니다.(x가 z에 영향을 받으므로 marginalization 연산)
사실 당연합니다.
latent(z)는 우리가 알지도 못하는 variable인데 모든 z에 대해 어떻게 적분(marginalization) 할까요..?
결국 우리는 아는게 별로 없어서 이런 문제가 생깁니다. Optimal 모델에서 파라미터도 모르고, latent variable z에 대한 정보가 없는 경우가 많습니다.
그리고 이런 intractability는 likelihood model이 조금만 복잡해져도 매우 흔하게 나타납니다. 안타깝지만 혹은 당연하지만 비선형성이 들어간 신경망은 이런 복잡한 모델에 속합니다.
다시돌아와서 VAE의 구조부터 살펴봅시다.
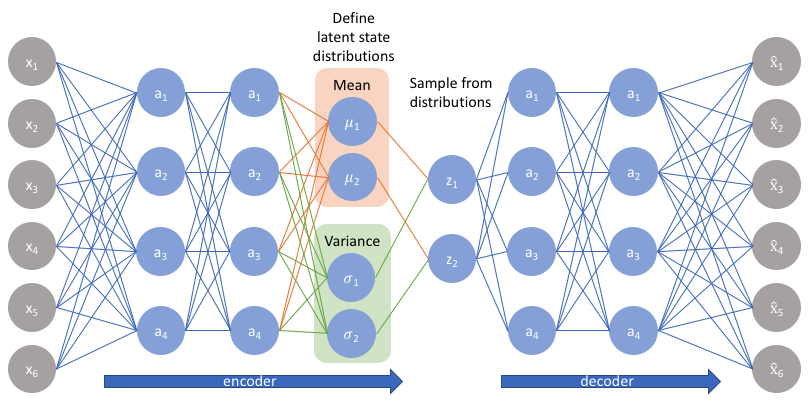
VAE는 Encoder와 Decoder로 이루어져 있습니다.
Encoder는 관측된 데이터 $x$를 받아서 Latent variable $z$를 만들어 냅니다.
Decoder는 $z$를 활용하여 $x$를 복원해 냅니다.
latent variable $z$는 무슨 의미일까요..?
예를들어 고양이의 사진을 기준으로 생각해봅시다.
고양이의 특징으로는 귀, 눈, 수염, 무늬 등 다양한 특징이 존재합니다.
Encoder는 위의 언급한 특징들을 바탕으로 $z$를 생성하고,
Decoder는 $z$를 바탕으로 데이터를 복원한다고 볼 수 있습니다.
Decoder 파트는 정규분포를 전제로 하고 있습니다.(Z에 의한 parameter를 가지겠죠?)
MLE를 활용하여 VAE모델의 parameter를 추정해봅시다. marginal log-likelihood를 사용해서 $p(x)$를 maximize하는 문제입니다.
앞서 말씀드렸다시피 z는 무수히 많은 경우가 존재하게 될것이고 때문에 위의 식은 그대로 사용하기 어렵습니다.
여기서 우리는 Variational Inference를 사용합니다.
Variational Inference의 강력한 점은 본디 posterior를 estimation하는 statistical inference였던 문제를 optimization 문제로 바꿔줍니다
여기서 insight를 얻을 수 있는 점은 Vi를 이용해서 기존의 문제를 optimize문제로 변경해주고(Deep learning이 optimize문제에 강력하니까),
이렇게 바뀐 문제를 iterative update 대신에
posterior $q(z|x)$
likelihood $p(x|z)$가 각각 encoder와 decoder인 Auto-Encoder로 모델링하여
이를 Gradient Descent를 이용하여 한번에 update 할 수 있습니다.
위와 같은 전략을 사용하여 문제를 해결한 것이 VAE 입니다.
EM algorithm을 사용하여 ELBO를 구할 수 있습니다.
일반적으로 $q(z)$를 정규분포로 많이 사용하겠지만
Data $x$ 가 고차원일 경우 모든 데이터에대해 동일한 $mean$과 $var$를 가정하게되면 데이터의 복잡성에 비해 모델이 너무 단조로워 학습이 굉장히 어렵습니다.
이러한 문제를 해결하기위해 $q$의파라미터를 $x$에 대한 함수로 생각해봅시다.
$q$를 위와 같이 설정하고 ELBO를 Maximize하는 방향으로 $q$를 학습하게 되면 $x$에 따라 $q$의 분포가 달라지게 됩니다.
$x$에 따라 $q$의 parameter가 바뀔테니 말이죠.
Encoder로 돌아와 봅시다.
Encoder에는 $x$를 input으로 하여 latent variable $z$의 mean과 var를 만들어내는 네트워크가 두 가지($f_μ,f_σ$) 존재합니다.
다음 단계는 이 확률분포로 부터 Sampling 하는 것인데.. Sampling연산은 미분가능한 연산이 아니므로 Back propagation을 사용할 수 없습니다.
NN으로 정의한 모델을 gradient descent로 푼다는 것은 모델이 parameter에 대해 미분이 가능하고 이는 모델이 어떤 의미에서는 deterministic하다는 것을 의미합니다.
즉, fixed parameter들에 대해 stochasticity는 input에만 있고 같은 input에 대해서는 항상 같은 output이 나와야 하는데 이 “sampling”이란 녀석은 모델 자체에 stochasticity를 넣어버리기 때문에 문제가 됩니다.
zero-mean Gaussian에서 noise를 추출하여 $f_μ,f_σ$가 산출한 mean과 var를 더하고 곱해줘서 sampled latent vector $z$를 생성합니다.
수식은 다음과 같으며 이와같은 과정을 reparameterization trick이라고 부릅니다.
noise sampling입니다. 이렇게 되면 역전파를 통해 mean과 var를 업데이트 할 수 있습니다.
다시 Decoder로 가봅시다.
Decoder는 Data $x$의 Posterior를 학습합니다.
하지만 Posterior를 학습하기엔 너무 어렵고 복잡해서 Vi를 이용한 근사를 사용하기로 했었죠?
위와같이 나타낼 수 있습니다.
아까 위에서 구했던 $logp(x)$식 처럼 정리하면 다음과 같이 표현 가능합니다.
사실 EM algorithm을 알고계시다면 위 식에서 동일한 확률변수에대한 KLD값은 항상 양수이므로 위 식을 아래와같이 변경할 수 있습니다.
부등식의 ELBO를 Maximize하면 우리의 목적인 marginal log-likelihood $logp(x)$를 최대화 하게 됩니다.
또한 위의 등식을 살펴보면(동일한 확률변수에 대한 KLD값에 대한 부분) ELBO를 최대화 한다는 의미는 KLD값의 최소화 즉 $q(z|x)$를 $p(z|x)$에 최대한 근사한다는 의미가 됩니다.
더 생각해보면
Maximum likelihood $logp(x|z)$ 문제를 푸는데,
Vi $q(z|x)$
그리고 Z에 대한 Prior$p(z)$ 사이의 차이가 최소가 되도록하는 Regularization term을 추가하여 optimize 문제를 푸는것으로 생각할 수 있습니다.
즉, 문제를 정의하고 나니 해석이 꽤 그럴듯하게 됩니다.
Maximum likelihood 문제는 결국 regression 문제로 생각하면 평균값으로 fitting해주는 문제가 되고 여기에 우리가 모델로 근사한 posterior와 prior 분포가 일치하도록 하는 제약이 추가되어 좀 더 나은 parameter를 찾고자 하는 것이죠.
계속 Optimize 언급을 했으니 이제 Optimize 해봅시다!
Loss function은 위의 목적함수를 그대로 가져와서 사용 하면 되므로 -를 붙여서 minimize한다고 생각하면 되겠죠..?
우변의 첫번째 항(기댓값에대한 항)을 Reconstruction loss로 부릅니다.
Encoder가 데이터를 받아와서 $q$로부터 $z$를 추출하는 것과
Decoder가 $z$를 받아서 원본 데이터 $x$를 복원하는 것 둘 사이의 Cross entropy를 나타냅니다.
두번째항의 의미는 $q$를 zero-mean Gaussian에 근사하게 만든다는 의미입니다.
VAE의 Loss function을 도식적으로 나타내면 다음과 같습니다.
Implement
FullCode는 여기서 보실 수 있습니다.

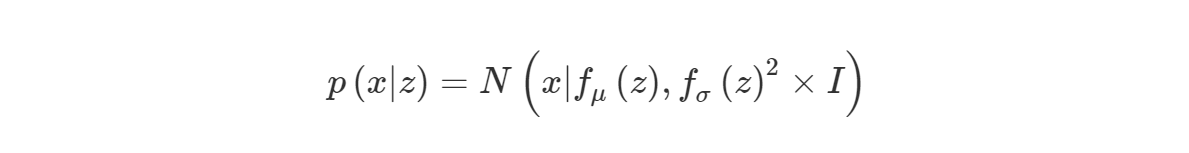
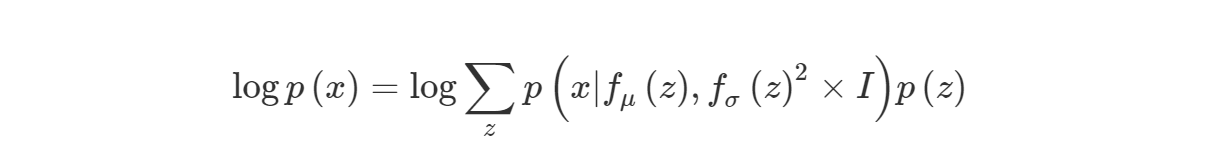
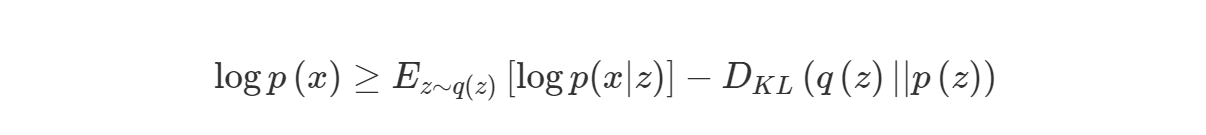
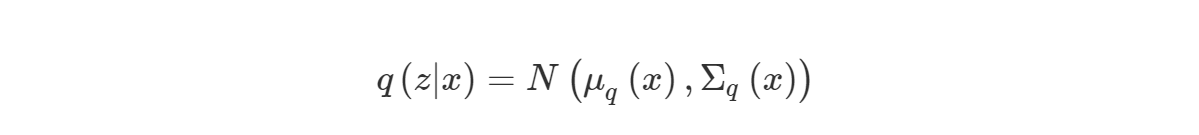
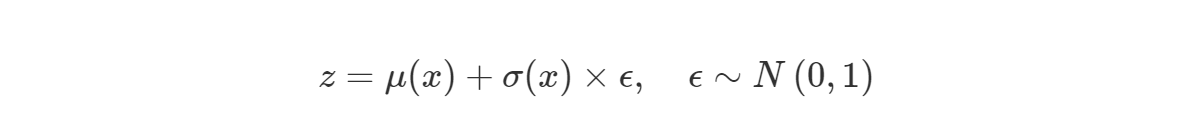
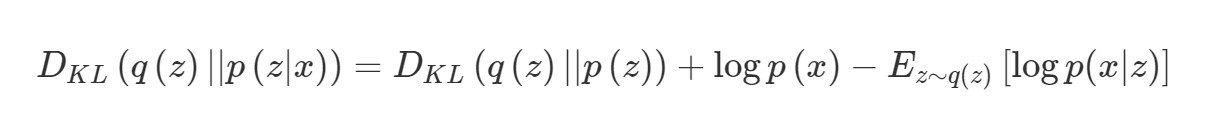
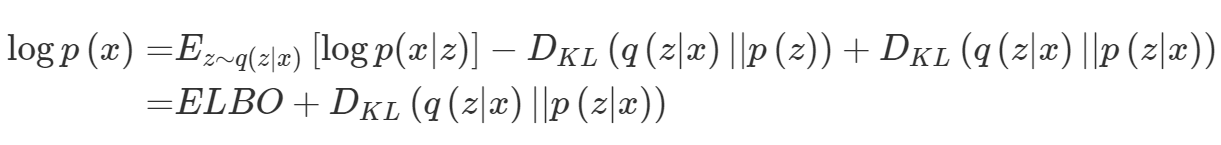
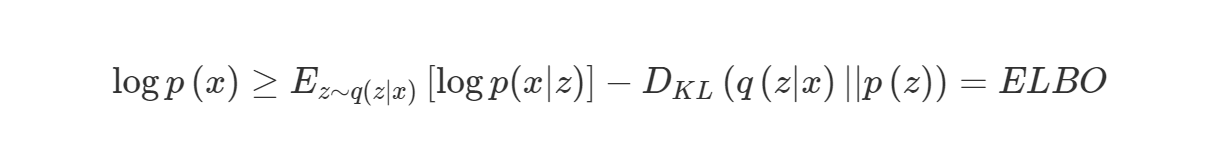
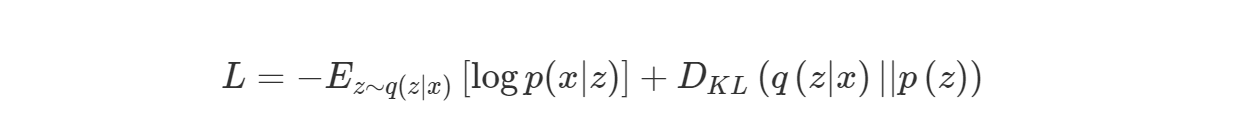


Comments