GAN
24 Oct 2019 | ganGenerative Adversarial Networks
SRGAN 논문을 읽기위해서 GAN에 대해 공부한 내용을 정리했습니다.
더 자세히 알고 싶으신분들은 Paper를 참고하세요.
GAN은 이름에서 알 수 있듯 서로 대립하며 생성하는 네트워크입니다.
다시 말하자면 생성자와 구분자가 존재하는데, 생성자의 목적은 실제 데이터의 분포와 가장 근사하는 분포를 모방해 내는 것이고 구분자의 목적은 생성자가 모방한 분포와 실제 데이터 분포를 구분하여 실제 데이터 분포일 확률을 뱉어내는 것입니다.
이 둘은 서로 대립하는 관계에있어서 서로의 성능을 발전시켜 나갑니다.
논문의 예시를 인용하면
지폐위조범(Generator)은 경찰을 최대한 열심히 속이려고 하고 다른 한편에서는 경찰(Discriminator)이 이렇게 위조된 지폐를 진짜와 감별하려고(Classify) 노력합니다. 이런 경쟁 속에서 두 그룹 모두 속이고 구별하는 서로의 능력이 발전하게 되고 결과적으로는 진짜 지폐와 위조 지폐를 구별할 수 없을 정도(구별할 확률 $p_d$=0.5)에 이른다는 것 입니다.
구별할 확률 $p_d$=0.5 라는 얘기는 실제 데이터의 분포 = 생성자가 생성한 분포 인 경우이며 구분자가 이 데이터가 실제 데이터인지 모방 데이터인지 알 수 없어서 1/2 확률로 찍게 되는(??) 경우입니다.
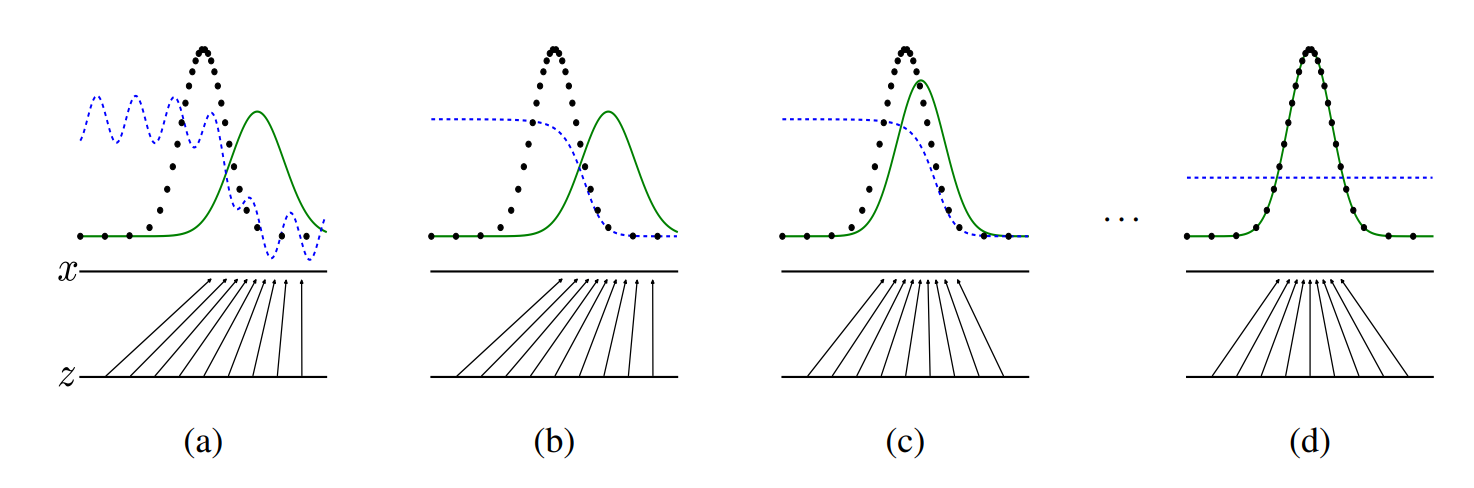
파란색 그래프는 discriminator distribution, 검은색 그래프는 data generating distribution, 녹색 그래프는 generative distribution를 나타냅니다.
밑에 화살표는 x = G(z)의 mapping을 보여줍니다. 그래프를 보면 알 수 있듯 학습이 진행됨에따라 점점 녹색 그래프가 검은색 그래프로 근사하게되고 완벽히 일치했을 때(즉 Global optimal 일 때) 구분자(D(x))=1/2 인 상태가 됩니다.
(1)번 수식은 GAN의 Cost function입니다. 즉, V(D,G) 에서 log안의 값들이 1이 되는게 가장 best case겠죠?
이렇게 되려면 Generator = minimize, Discriminator = maximize 해야 합니다.
For G fixed, the optimal discriminator D is
(2)번 식의 유도는 (1)번 식으로 할 수 있습니다.
$alogy + blog(1-y)=0$ 를 미분하게 되면 $a/y - b/(1-y)=0$ 이 될 것이고,
이를 $y$ 에대해 정리하면 $(a+b)y = a$ 즉, $y = a/(a+b)$ 꼴이 되어 (2)번 식처럼 됩니다.
결국 $min_G max_D V(G,D)$에서 안 쪽의 max 문제부터 풀어주면 문제가 다음과 같이 reformulate 됩니다.
Main Theorem
D가 Optimal에 도달했으니, G의 입장에서 minimize를 풀어봅시다.
For $P_g = P_d, D*_G(x) = 1/2$ 임을 위에서 증명했고,
$C(G) = C(G) + log(4) - log(4)$이고, $E_x∼p_d[−log(P_d(x)/P_d(x)+P_g(x))]+E_x∼p_g[−log(P_g(x)/P_d(x)+P_g(x))] + log(2) + log(2)$ 임을 이용해
$log(2)$들을 각 expection안에 넣어주면 아래의 (5)번식을 유도할 수 있습니다.
! KL 이란?
Kullback–Leibler divergence의 줄임말로 어떤 두 가지 확률분포의 차이를 나타낼 때 쓰입니다.
자세한건 Wiki를 참조해주세요. 위 KL들을 아래의 (6)번 식으로 나타낼 수 있습니다.
여기서 D = KL 입니다. 양변에 2를 곱하면 위의 식 모양과 똑같죠?
JSD 또한 더 궁금하시다면Wiki를 참조해주세요.
앞서 정의한 V(D,G)를 풀게 되면 (Global optimal를 찾으면) Generator가 만드는 Probability distribution($P_g$)이 Data distribution($P_d$)와 일치할 수 있게 되고, 논문에선 신경망(MLP)를 사용하여 G,D를 정의 각각 fix한 상태로 번갈아가며 문제를 풀게 됩니다.
우리는 $P_d - P_g ≥ 0$ 임을 알고 있습니다. 즉, $P_d = P_g$ 일때만 제외하면 Convex function이 되므로(모두 양의값이니까) 기존의 인공지능처럼 Backpropagation을이용하여 모델을 optimize할 수 있게 됩니다.
자세한 설명은 참조한 블로그에서 카피한 내용으로 대체하겠습니다.
Implement
FullCode 는 여기서 보실 수 있습니다.
GAN으로 생성한 mnist 데이터셋



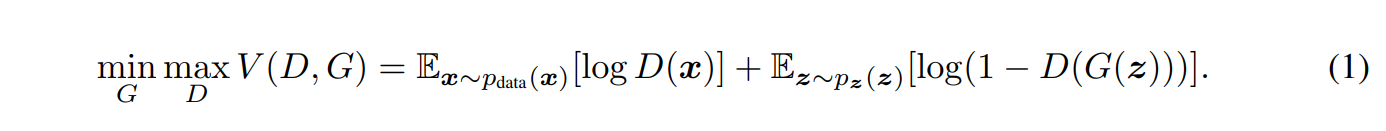
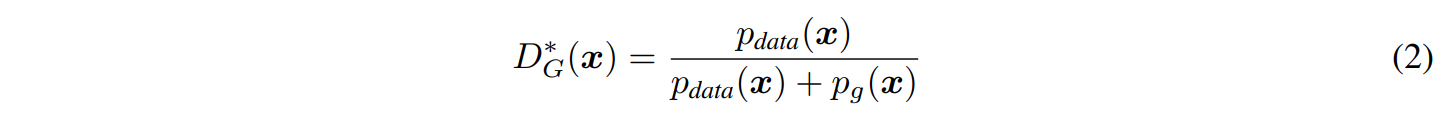
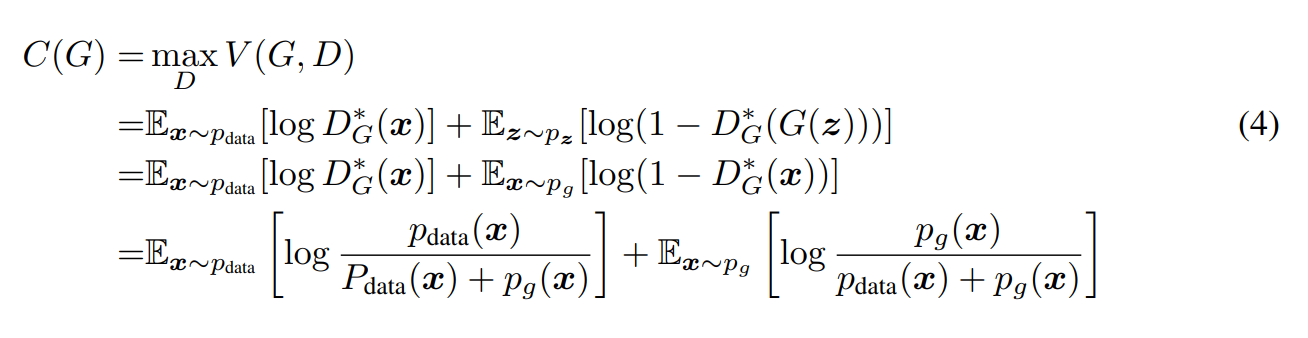
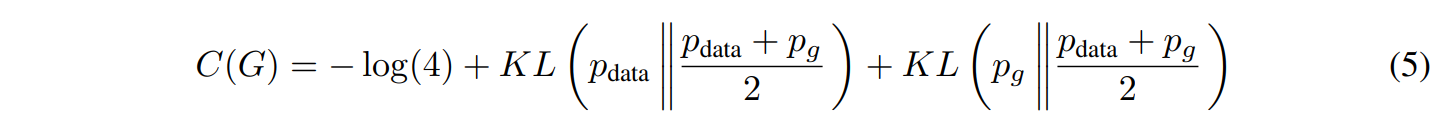
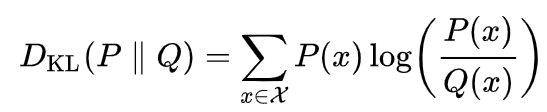
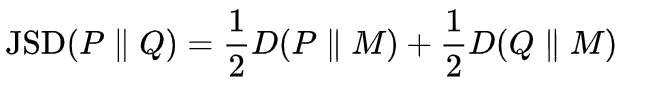
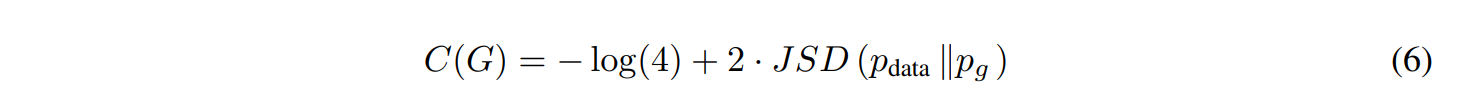
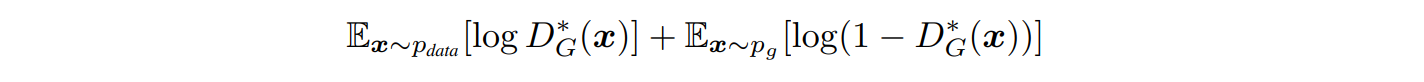

Comments