Accurate Image Super-Resolution Using Very Deep Convolutional Networks(VDSR) - Review

VDSR 논문리뷰 입니다.

서울대 로고가 뜨길래 놀랬는데 실제로 한국분이 쓰신 논문입니다.

Abstract

매우 정확한 SISR에 대한 방법을 제시합니다.

VGG에서 영감을 받았고, 논문 제목처럼 Very Deep CNN(20 weight layer)을 이용합니다.

이러한 Very Deep model을 학습시키기 위해 논문에서는 크게 두 가지 방법을 제시합니다.

1. Residual Learning
2. Gradient Clipping

Proposed Network

SR에는 ill-posed problem이 있습니다.

! ill-posed problem이란?

영상에 가해진 degradation으로 인해 이를 되돌리는 것은 매우 “어려운데”, 여기서 어렵다는 것은 “ill-posed” inverse problem 이라는 뜻입니다. 예를 들어 Single Image Super-Resolution (SISR)은 대표적인 ill-posed problem으로 방정식의 변수가 독립적으로 구성할 수 있는 식의 갯수보다 많은 경우입니다. 좀 더 구체적으로는 H의 row 수에 비해 column의 수가 훨씬 많기에 x의 해가 무한히 많을 수 있어서 진짜 x를 특정하기 어렵다는 것으로, 한 장의 저해상도 이미지에 대응할 수 있는 고해상도 이미지는 다양한 경우의 수가 있다는 예시로 이해하시면 쉽습니다.

출처 : Jaejun Yoo’s Playground

대부분의 이미지는 center pixel을 잘 추론하려면 surrounding pixel들이 필요합니다.

때문에 이미지 경계 근처 픽셀의 경우 이 관계를 최대한 활용할 수 없어서 Super Resolution방법의 경우 대부분 결과 이미지를 crop 하게 됩니다.

그러나 이 방법은 필요한 surround 영역이 매우 큰 경우 유효하지 않고, crop한 후 이미지가 너무 작아 시각적으로도 만족스럽지 않습니다.

이러한 문제를 해결하기 위해 conv연산 이전에 zero padding하여 모든 feature map(output image를 포함하여)의 크기를 동일하게 유지합니다.

(실제로 제로패딩은 꽤나 잘 작동합니다.)

이미지 경계 근처의 픽셀도 정확하게 예측한다는 점에서 이 논문의 방법은 대부분의 방법과 다르다고 할 수 있습니다.

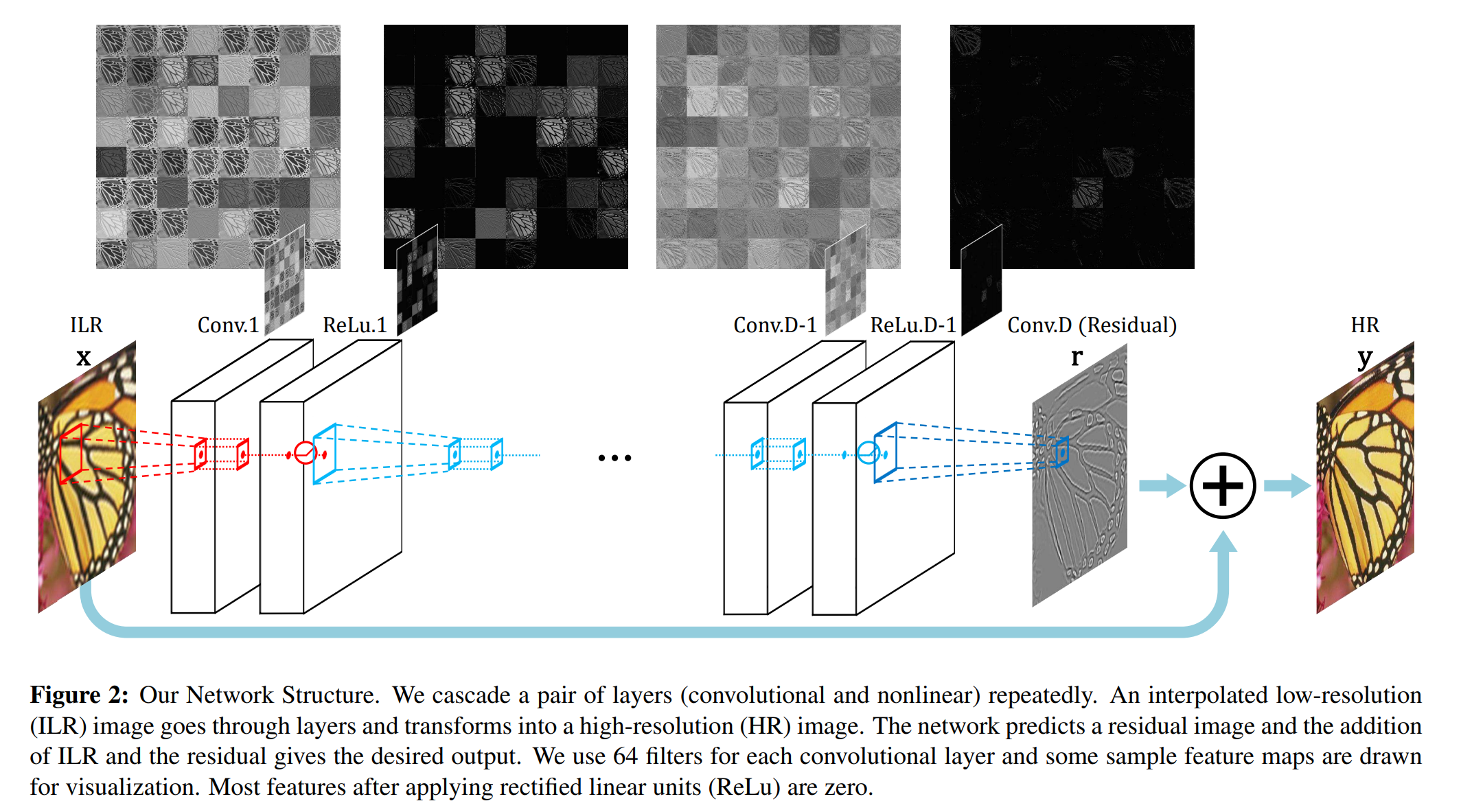
이미지의 세부 사항이 예측되면 입력 ILR(Interpolated Low Resolution) 이미지에 다시 추가되어 최종 이미지 HR를 제공합니다.

Training

모델의 최적 매개변수를 찾기 위해 최소화해야 하는 목표를 설명합니다.

$x = ILR, y = HR , z = f(x)$이고,

우리의 목표는 model f 를 잘 학습시켜 z를 예측하는 것입니다.

MSE를 사용하는데 여기서는 $1/2(y-f(x))^2$이 됩니다.

SRCNN(CNN을 최초로 SR에 적용시킨 논문)에서 이미지가 삭제되고 output이 학습된 feature에 의해 생성되므로 network는 input detail을 보존해야 합니다.

논문에서는 VDN(Very Deep Network)를 사용하므로 layer의 depth가 깊어지면 생기는 Gradient Vanishing/Exploding 문제가 치명적으로 작용합니다.

이를 해결하기 위해서 Abstract에서 제시했던 두 가지 방법을 적용합니다.

간단히 Residual Learning으로 이 문제를 해결할 수 있습니다.

in/output image가 유사하기 때문에,

우리는 residual image $(r) = y - x$ 로 정의합니다.(대부분의 값이 0이거나 매우 작은 값)

우리는 이 $(r)$을 예측하려 합니다.

Loss function = $1/2(r-f(x))^2$ 가 됩니다.(아마 Predict image(SR)인 f(x)를 Residual image와 유사하도록 학습하겠다는 뜻인 것 같습니다.)

네트워크에서 이는 Loss layer에 다음과 같이 반영됩니다.

Loss layer는 residual estimate, network input(ILR), ground truth (HR) 세가지 input을 받는다.

Loss는 reconstruction 된 이미지(network input & output 의 합)와 GT사이의 Euclidean distance로 계산된다.

backpropagation에 기반한 mini-batch gradient descent를 사용하여 regression 목표를 optimizing하는 방향으로 학습을 수행한다.

VDN에 대한 높은learning rate는 현실적으로 원하는 목표에 수렴하지 못할 수 있습니다.

SRCNN이 3개 이상의 layer를 사용하는 것에 대해 우수한 성능을 보여주는 것을 실패했습니다.

여러가지 이유가 있겠지만 한 가지 가능성은 네트워크가 수렴하기 전에 학습 절차를 중단했을 수 있습니다.

lr = $10^-5$로 너무 작아서 네트워크가 일주일내로 수렴하기 힘들었을 것입니다.

대부분의 학습 속도를 높이기 위해 학습률을 높이는것은 당연한 행동이지만, 단순히 학습률을 높게 설정하면 gradient vanishing/exploding 문제가 발생합니다.

따라서 우리는 저런 문제 없이 학습 속도를 높이기 위해 adjustable한 Gradient Clipping(이 논문의 두번 째 핵심)을 제안합니다.

gradient를 제한하는 방법에는 여러가지가 있겠지만, 일반적인 전략 중 하나는 개별 gradient를 사전 정의된 범위 [-θ,θ]로 clipping 하는 것입니다.

훈련에 일반적으로 사용되는 SGD에다 learning rate를 곱하여 step size를 조절합니다.

높은learning rate이 사용되면 gradient exploding을 피하기 위해 θ를 작게 조정합니다.

그러나learning rate이 작아질수록 annealed됨에 따라 effective gradient(gradient *learning rate)가 0에 가까워지고 learning rate가 기하학적으로 감소하면 수렴하는데 엄청난 반복이 필요하게 됩니다.

최대 수렴 속도를 위해 gradient를 [-θ/γ,θ/γ]로 자른다.

γ(gamma) = 현재 learning rate

조정 가능한 gradient clipping은 수렴 절차를 매우 빠르게 만듭니다.

3 layers SRCNN은 훈련하는데 며칠이 걸리지만, 20layer의 우리 모델은 4시간내에 완료할 수 있습니다.

Residual-Learning

입력으로 이미 저해상도 이미지가 있으므로 SR의 목적을 위해 high-frequency component를 예측하는 것으로 충분합니다.

residual predict의 개념은 이전 방법에서 사용되었지만,

deep learning에 기반한 SR Framework와 관련해서 연구되진 않았습니다.

residual image를 학습하는 network 구조를 제안하고, 이제 이 방법이 CNN에 미치는 영향에 대해 알아봅니다.

첫 째, residual network가 훨씬 빠르게 수렴한다.

residual 및 표준 network 를

depth = 10(weight layer), scale factor = 2 에서 비교해봅니다.

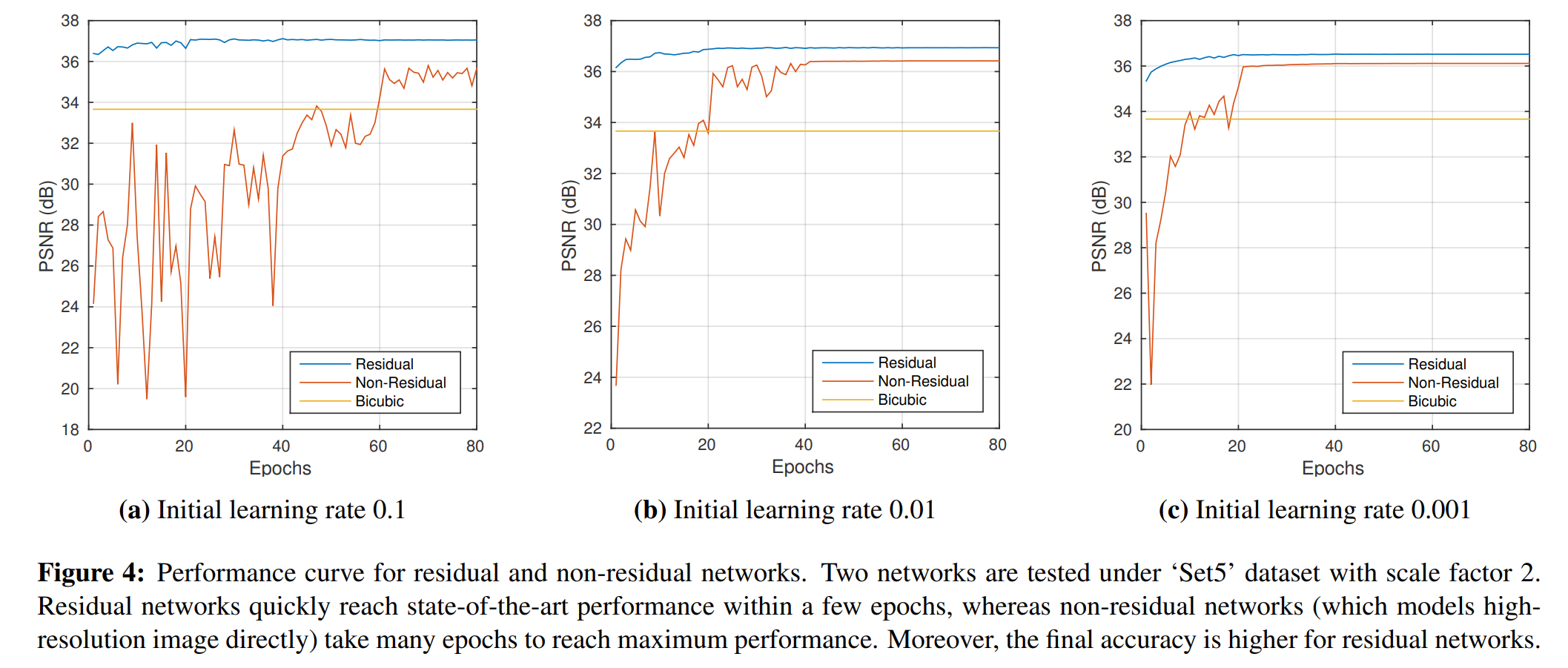
다양한 learning rate에 대한 성능 곡선이 Fig.4에 나타나있습니다.

둘 째, 수렴에서 residual network는 우수한 성능을 보입니다.

Fig.4에서 residual network는 훈련이 완료되면 더 높은 PSNR(성능지표중 하나)를 제공한다.

마지막으로, 작은 learning rate이 사용되면 주어진 epoch 내에 네트워크가 수렴하지 않습니다.

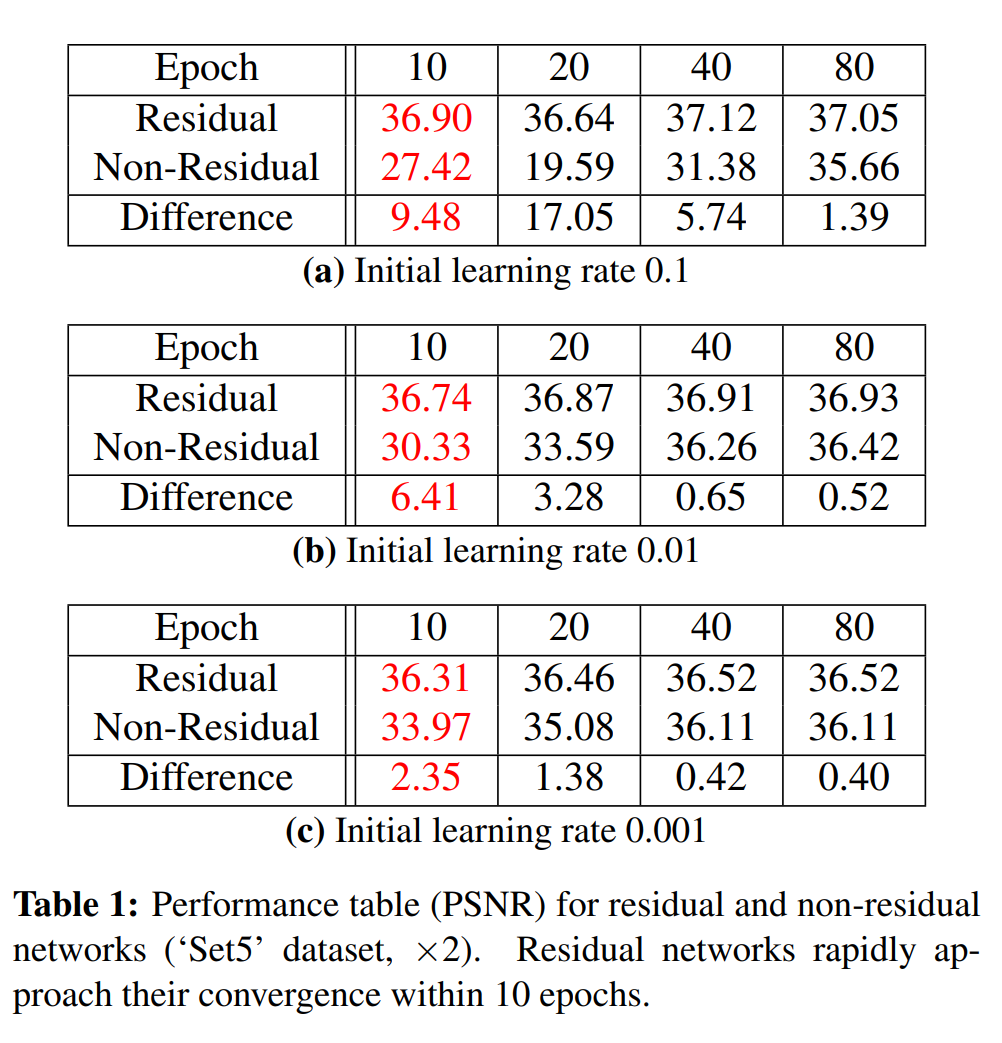
초기learning rate = 0.1을 사용하면 residual network의 PSNR이 10epoch 내에 36.90에 도달합니다.

하지만 0.001을대신 사용하면 network는 같은 수준의 성능에 도달하지 못합니다. (80epoch 이후 성능은 36.52 Table.1 을 참고)

비슷한 방식으로 residual network와 non-residual network는 10 epoch 이후 극적인 성능 차이를 나타냅니다.