Spectral-based GNN
21 Jul 2021 | GNNSpectral-based GNN
신호처리를 Graph domain에서!
그렇다면 signal(신호)는? graph node !
푸리에변환, 라플라스 변환 등을 적용할 예정이다. (공수에서 배웠지만 다까먹은 그것)
Laplacian Matrix
우선 라플라시안 행렬 얘기부터 시작해야한다.
그래프를 표현할 때 보통 인접 행렬을 사용하는데, 이를 대신해서 사용한다고 생각하면 편하다.
우선 라플라시안 행렬은 인접 행렬에 노드의 차수 정보를 추가한 행렬이다.
우선 여기서 전제로 무방향 그래프를 깔고 간다.
라플라시안 행렬의 정규화 버전을 무방향 그래프의 수학적 표현이라고도 한다.
\[L = I_n - D^{-1/2}AD^{-1/2}\]- $D$ : 노드의 차수를 표현하는 대각 행렬
- 정규화된 라플라시안 행렬은 positive semi-definite
따라서 위 행렬을 아래와 같이 분해 가능하다.
\[L = U\Lambda U^T\]- $U$ : 고유벡터
- $\Lambda$ : 고유값을 원소로 가지는 대각행렬
위 행렬의 고유벡터는 orthonormal 하므로 $UU^T = I$ 이다.
이제 여기서 구한 정규화된 라플라스 행렬 $L$과 고유 벡터 행렬 $U$를 spectral-based에 사용하게 된다.
- 대표적으로 사용되는 예시가 L의 두 번째로 작은 eigenvalue를 통해 graph cut을 한다고 한다.
- 여기서 graph cut에 대한 내용이 나오는데 이걸 또 다뤄 보자.
(당장은 라플라시안 행렬이 무슨 소린지 모르겠어도 괜찮다. 밑에서 다시 나온다.)
Graph Cut
그래프를 ‘‘잘’’ 분할 하려면 어떻게 해야 할까?
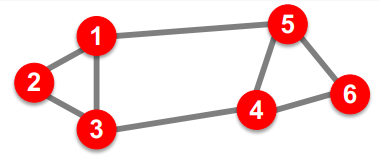
예를 들면 이런 그래프가 있다고 하자.
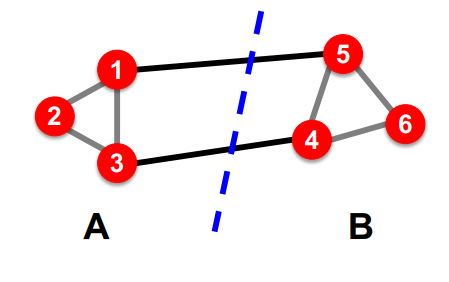
굳이 쪼개자면 이렇게 쪼개고 싶긴 하다.
이걸 좀 합리적인 이유를 통해서 표현하자면
- 그룹 내의 연결 수를 최대화 하고
- 그룹 사이의 연결 수를 최소화 하는 분할이다.
그렇다면 ‘Cut’ 이란 무엇일까?
Cut : 어떤 그룹에서 다른 그룹으로 가는 Edge(결국 다른 그룹사이에 있는 edge들의 가중치 합이다.)
\[cut(A,B) = \sum\limits_{i\in A, j\in B}w_{ij}\]그럼 Cut은 어떤 기준으로 하면 좋을까?
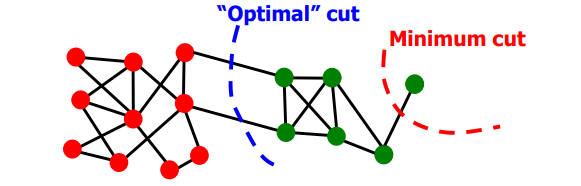
- Minimum cut : weight 제일 작은 기준으로 그룹을 분할하자.
- 솔직히 딱봐도 별로다.
- Conductance : 각 그룹의 볼륨에 대한 그룹간의 연결성을 고려해서 분할하자.
- 그러니까 A, B 두 그룹의 볼륨(그룹 내의 sum of weight degree)을 나눠줌으로써 minimum cut의 전체를 고려하지 않고 자르는 문제를 좀 방지할 수 있다.
- 근데 optimal conductance는 NP-Hard이다.(최적화가 다그렇지 뭐..)
우선 여기까지 해놓고 다시 인접 행렬로 돌아오자.
인접 행렬과 어떤 R^n space의 벡터를 가져와서 연산하면 어떤 의미를 가질까?
수식을 보면 알겠지만 Ax = y 의 의미는,
y가 i의 연결된 이웃들 $x_j$의 합으로 나타낼 수 있다는 것이다.
그러니까… X들을 노드로보게 되면 Ax 자체가 인접행렬 x 노드 이므로 연산 결과인 $y_i$ 는 $i$ 번째 노드와 연결된 다른 노드들의 합으로 생각할 수 있다. (0,1 로 이루어진 인접 행렬과 노드 $x_1, x_2, x_3, …, x_n$ 을 생각해보자.)
위 식을 살펴보면 어디서 많이 본듯한 꼴이다.
바로 고유벡터와 고윳값의 형태이고 여기서 벡터 X를 인접행렬 A의 고유 벡터로 말할 수 있다.
여기서 재밌는 예시가 나오는데,
모든 노드의 차수가 ‘d’ 이고, 벡터 X가 (1,1,1,…,1) 이라고 가정하자.
Ax = (d,d,d,d,d) 가 되고 따라서 $\lambda = d$ 가 된다.
왜냐면 A의 각 행은 edge를 나타내게 되는데, edge의 합이 곧 d이기 때문이다.
그리고 이 때 고윳값 d는 A의 가장 큰 고윳값이다.
Matrix Representation
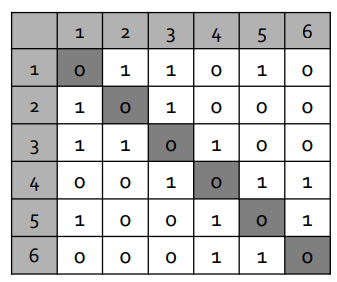
기존의 우리가 가진 그래프를 인접 행렬로 나타내면 다음과 같다.
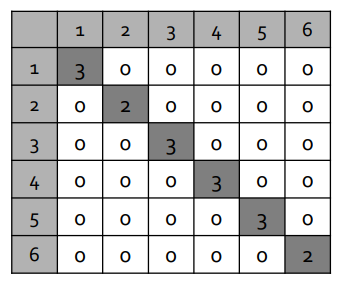
그리고 Degree Matrix로 다음과 같이 차수의 형태로 나타낼 수 있다.(위에서 보인 것 처럼 인접행렬의 각 행의 합 = degree)
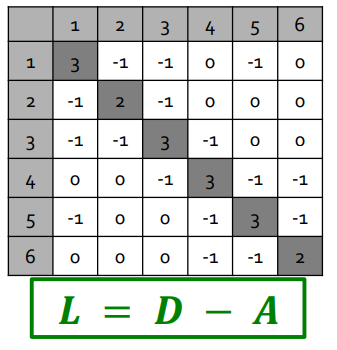
그리고 이를 이용해서 라플라시안 행렬을 다음과 같이 정의할 수 있다.
라플라시안 행렬은 다음과 같은 특징을 가진다.
- 우선 각 행의 합이 0이다.(당연하게도 Degree Matrix - 인접 행렬이니까.)
- Symmetric
- n(node 개수)개의 고윳값을 가짐.
- 모든 고유 벡터가 실수이며 직교한다.
또한 라플라시안 행렬 L은 다음과 같은 특성을 가지는데.
- 모든 고윳값이 0 이상이다.
- $x^TLx = \sum\limits_{ij}L_{ij}x_ix_j \geq 0\ \ \ for \ every\ x$
- L은 다음과 같이 표현할 수 있다. $L = N^T\cdot N$
이건 그냥 positive semi-definite를 3가지 방식으로 말한 것이다.
$\lambda_2$ Problem
일단 갑자기 $\lambda_2$가 나왔는데 우선 이 것을 찾아서 더 많은 이점을 가질 수 있다는 것만 알고있자.
$\lambda_2$는 다음과 같이 표현 가능한데,
사실 별거 없다. 일단 M은 symmetric이고,
아래의 성질을 보면 $x$와 $w_1$은 수직이어야 하며 오른쪽의 수식의 값을 최소화 하는 x는 고유 벡터이고 이 때 $\lambda_2$의 값이 오른쪽 수식이다.
행렬에 M 대신 L을 넣어주고, $x^TLx$의 결과는 다음과 같다. (증명은 아래 레퍼런스에서 18p 참조)
\[\sum\limits_{(i,j)\in E}(x_i - x_j)^2\]x를 unit vector로 하고 두 위 식과 결합하면 최종적인 $\lambda_2$에 대한 식은 다음과 같다.
이제 다시 Optimal cut 문제로 돌아와보자.
우선 벡터 y를 다음과 같이 정의한다.
이제 cut problem은 다음과 같이 최소화 되는 y를 찾는 문제로 정의된다.
Rayleigh Theorem에 의해 위 식을 최소화 시키는 y는 라플라시안 행렬 L에 대해 $\lambda_2$는 f(y)의 최소값이 되고, 이를 최소화 하는 벡터 y는 그에 해당하는 고유 벡터가 된다.
그리고 이 두 속성을 이용한 클러스터링은 conductance를 최소화 한다고 한다.

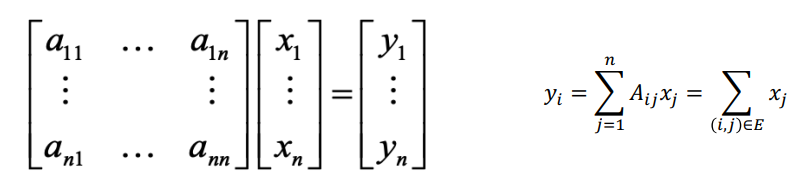
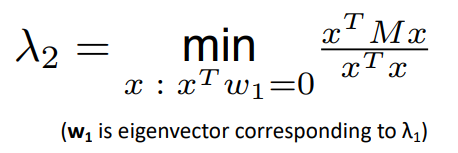
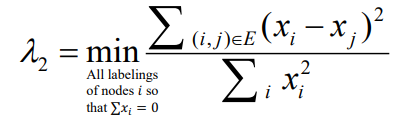
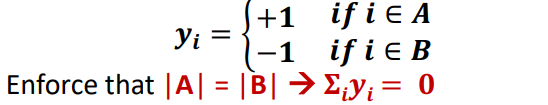
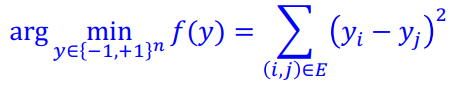

Comments