Matrix Factorization
06 Jul 2021 | RecommendLow Rank Approximation(LRA)으로 접근함.
LRA는 Matrix Factorization을 통해 행렬을 분해하고 $X = UV^T$ 이 행렬들을 통해 다시 reconstruction 하기 위한 방법임.
Why Low Rank?
$m\times n$ 행렬 $X$를 $m\times k$ 행렬 $U$와 $k\times n$행렬 $V^T$로 표현할 수 있는데, 이 경우 파라미터 수는 $k(m+n)$ 이다.
우리의 행렬중 관측치가 이 보다 많으면 reconstruction이 가능하지만, 대부분의 경우가 불가능하고, 이를 위해 가능한 $k$를 작게 즉, low rank로 가져가는 것이 reconstruction에 유리하다고 이해했다.
Why use Nuclear Norm?
그렇다면 왜 Nuclear Norm을 최소화 하는 걸까?
Nuclear Norm은 Singular Value에 대한 L1 norm으로 해석 가능한데, 벡터에서 L1 norm은 0에 가까운 요소들을 0으로 만든다 즉, 벡터를 Sparse하게 만든다.
이를 통해 Nuclear Norm을 통해 Sparse한 Matrix를 만들도록 제약조건을 걸고 이는 Low Rank Matrix Approximation을 위해 하는 것으로 이해할 수 있다.
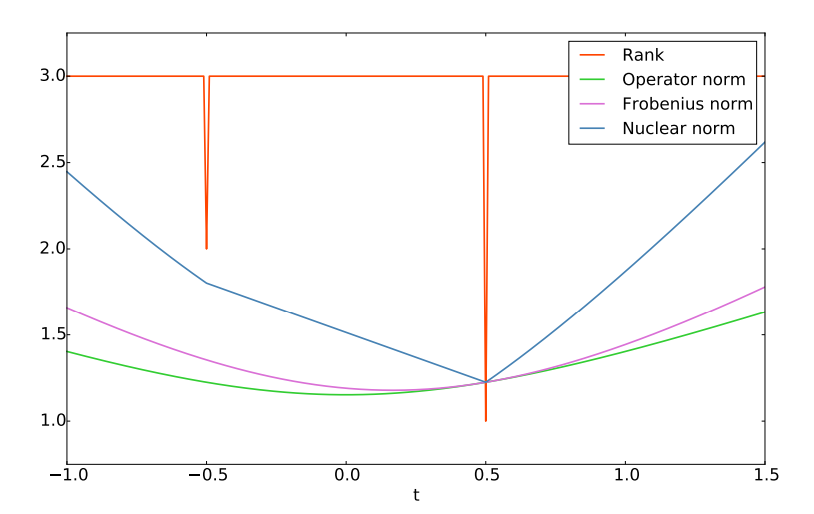
다음 행렬의 Rank를 최소화하는 t값은 nuclear norm을 최소화 하는 것과 동일 하다는 것을 그래프를 통해 확인할 수 있다.

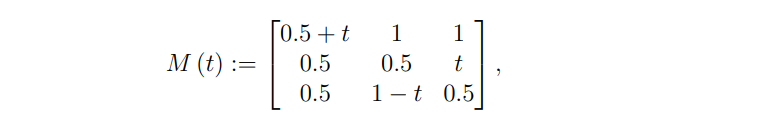
Comments