Actor-Critic

REINFORCE

Policy based 방법의 대표적인 고전 알고리즘 REINFORCE에 대해 알아봤습니다. 대부분의 책에선 REINFORCE가 너무 오래돼서 안쓴다고 하지만 메인 도메인을 강화학습에서 조금만 눈을 돌려보면 AutoML이라는 분야에서 쓰이는 것을 발견할 수 있습니다.

제가 예전에 리뷰했던 페이퍼인 Neural architecture search with reinforcement learning 라는 논문에서 RNN 컨트롤러를 학습시킬 때 이 알고리즘이 사용됩니다.

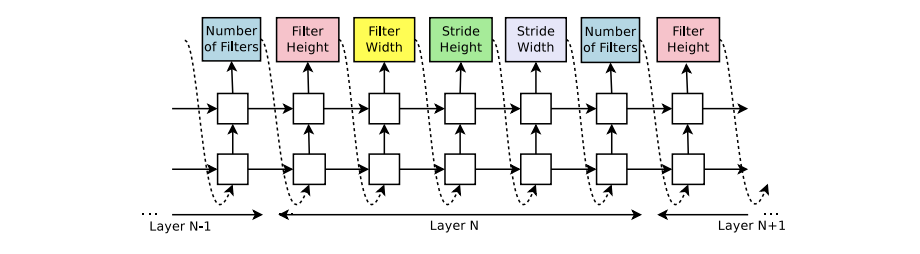
REINFORCE의 단점은 대표적으로 다음과 같습니다.

• Monte-Carlo 기반에서 오는 High Variance
• Loss에 들어간 $G_t$를 구하기 위해 걸리는 긴 시간과 높은 코스트
• On-policy 방법이라 효율성이 떨어짐

그래서 이 분산을 좀 줄이기 위한 노력의 결과인 Actor-Critic에 대해 알아봅시다.

아무리 봐도 저 $G_t$ 녀석이 문제인 것 같으니 좀 바꿔봅시다.

우리에겐 벨만 방정식이라는 친구가 있으니까 $G_t$를 $Q-function$으로 치환할 수 있습니다.

자세한 과정은 아래 참고.

굳이 설명을 하자면 대부분의 강화학습 알고리즘의 전개 방식은 다음과 같은 프로세스를 따릅니다.

• policy를 bayes rule로 적절히 쪼갠다.
• 적분 구간을 쪼개진 policy에 맞게 나눈다.
• 이제 나눠진 적분 식을 다른 식으로 치환하거나 불필요한 구간에 대한 적분을 날린다.

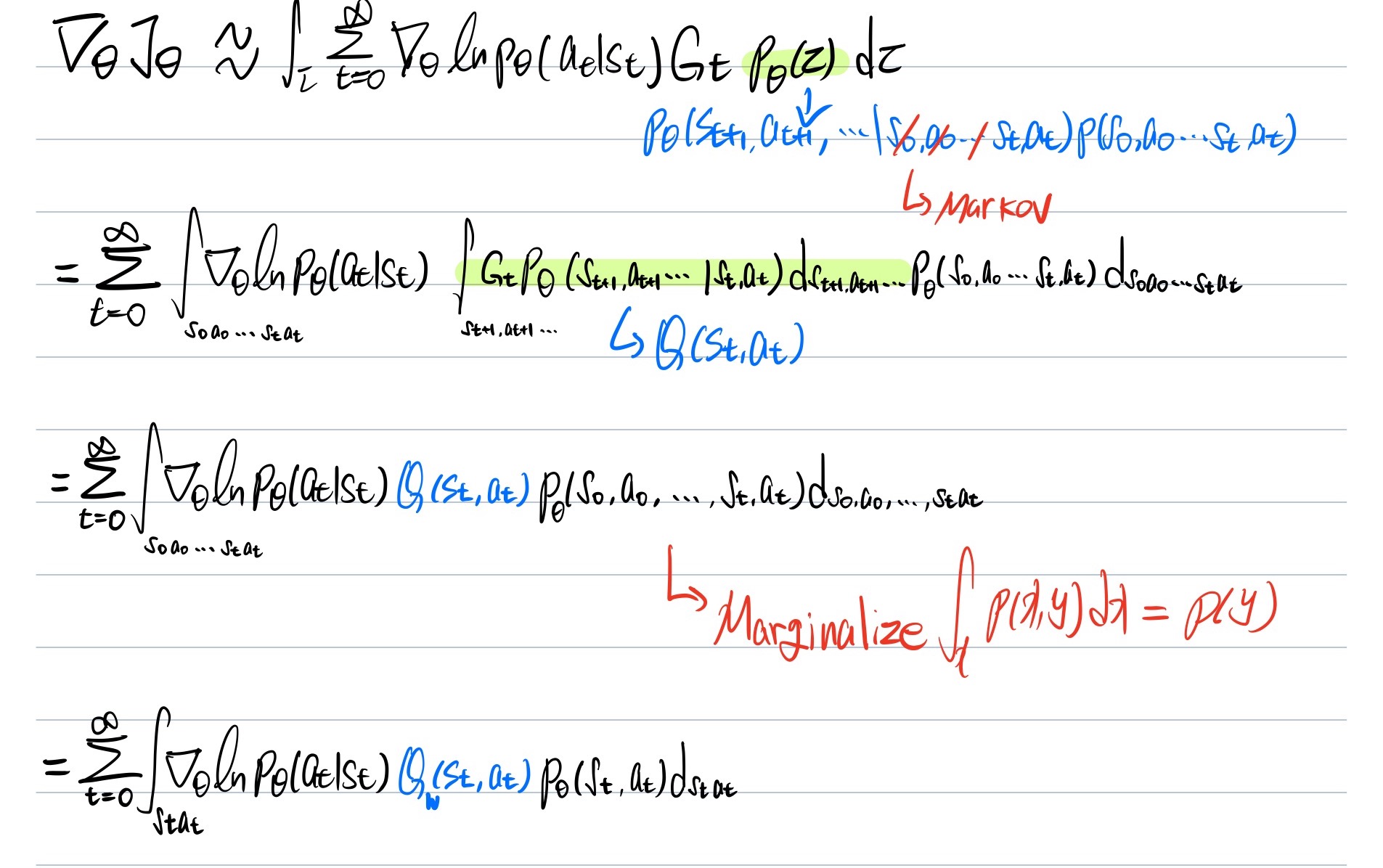
따란~ 그런데 Q도 어차피 정의상 $G_t$의 Expectation 형태라 코스트 비싼건 마찬가지니까 그냥 policy 처럼 parameterized해서 Gradient 업데이트 하자! 라는게 메인 아이디어 입니다.

그래서 Actor-Critic은 Actor(policy)와 Critic(Q-function) 두 개의 파라미터를 업데이트하는 학습 과정을 갖습니다.

SARSA를 통한 업데이트를 하므로 목적 함수는 다음과 같습니다.

State Action Reward (next)State (next)Action 의 형태이기 때문에 SARSA!

요기서 감마앞에 max가 붙으면 Q-learning과 동일한 수식입니다.

이 차이를 이해하셨다면 공부를 정말 열심히 하신 겁니다!

사실 SARSA에 Max가 붙지 않(못?)는 이유는 On-policy 방식이기 때문입니다.

또한 $\gamma Q_w(s_{t+1},a_{t+1})$를 TD-target이라고도 부릅니다. 현재 Q값을 next Q값에 가깝게 만들어주는게 목적입니다.

Actor는 policy를 뜻하므로 마치 영화배우가 액션을 하는 것과 같고, Critic은 Q-값을 통해 비평가가 평점을 매기는 구조와 같습니다.(이름을 참 잘 지었다고 생각했습니다.)

전체적인 학습 프로세스는 다음과 같습니다.

Initialize $\theta, w$

1. Actor Update
   • $\theta \leftarrow \theta+\alpha\nabla_\theta lnp_\theta(a_t\vert s_t)Q_w(s_t,a_t)$
2. Critic Update
   • $w \leftarrow w - \beta\nabla_w (R_t+\gamma Q_w(s_{t+1},a_{t+1}) - Q_w(s_t,a_t))^2$

Actor-Critic 구조는 biased, low variance 입니다.

직관적으로 $G_t$를 얻기 위한 에피소드를 끝까지 진행하는 방식이 아닌 next step의 Q값을 통한 업데이트 방식은 REINFORCE에 비해 낮은 분산을 얻을 수 있게 합니다.

그러나 $Q^*$가 아닌 파라미터화 된 Q를 사용하기 때문에 정확한 값이 아님으로 인해 발생하는 bias가 존재합니다.(또한 REINFORCE때 처럼 $\gamma^t=1$로 가정한 부분도 여전히 bias를 유도하게 됩니다.)