Model Free Prediction
26 Nov 2020 | Reinforcement LearningSummary
목표 : Model Free 즉, MDP에 대한 정보가 없는 상황에서 Prediction(주어진 Policy에 대한 Value-function을 찾는 것) 하자.
핵심은 딱 하나 $Q^$만 있으면 greedy 가 optimal policy인데 어떻게 $Q^$를 구할까? MC & TD가 샘플을 통해 $Q^*$를 구하는 방법임.
- MC has high variance, zero bias
- Good convergence properties
- Even with function approximation (대충 딥러닝 써도 수렴 잘된다는 뜻)
- Not very sensitive to initial value
- Very simple to understand and use
-
TD has low variance, some bias
-
Usually more efficient than MC
-
TD(0) convergence to $v_\pi(s)$
- But not always with function approximation
- More sensitive to initial value (초기값을 통해 $v(s)$를 업데이트함)
-
bias가 있어도 과연 잘 동작한다고 할 수 있느냐?
왜냐면 bias로 인해 잘못된 값으로 수렴할 수도 있으니까
다행히 잘 동작한다고 말할 수 있다고 함. 실버 교수님강의에서 증명하진 않음
Monte-Carlo
러프하게 말하면 실제 값(return ‘G’)을 통해 추정하는 방법이다.(G를 구해서 평균내자)
\[E[x] = \int xp(x)dx \approx \frac1N\sum\limits_{i=1}^Nx_i\]- MC는 Model-Free 방법론이다. MDP(transition, reward)에 대한 정보가 없음
- 에피소드를 끝까지 해봐야함.(no bootstrapping)
- 에피소드가 ‘끝’이 있어야 적용할 수 있음.
위 수식을 Q-function에 적용해보자.
\[Q(s,a) = \int G_tp(s_{t+1}:a_T\vert s,a)ds_{t+1}:a_T \approx \frac1N \sum\limits_{i=1}^NG_t^{(i)}\]즉 샘플 $G_t$를 계속해서 뽑다보면 큰수의 법칙에 의해 Q값에 수렴한다는 것이다.
위에서 적은 것 처럼 $G_t$가 샘플 하나이기 때문에 에피소드가 끝이나야 업데이트가 가능하며, unbiased 이지만 variance가 크다는 문제점을 가지고 있다.
First-Visit Monte-Carlo
-
한 에피소드에서 처음으로 방문한 상태에만 카운트 $N(s)\leftarrow N(s)+1$
-
리턴을 더해주고 $S(s)\leftarrow S(s)+G_t$
-
평균냄 $V(s) = S(s)/N(s)$
Every-Visit Monte-Carlo
- 한 에피소드에서 방문한 모든 상태를 카운트 $N(s)\leftarrow N(s)+1$
- 에피소드가 끝나면 리턴을 더해주고 $S(s)\leftarrow S(s)+G_t$
- 평균냄 $V(s) = S(s)/N(s)$
딱히 뭘 쓰든 상관 없다고 강의에서 언급함. 어쨌든 $V(s)$에 수렴.
단, 모든 상태에 방문한다는 전제 조건이 필요함.
Incremental Monte-Carlo Updates
\[V(s_t) \leftarrow V(s_t)+\alpha(G_t-V(s_t))\]- $G_t-V(s_t)$는 에러텀, $\alpha = \frac1N(s_t)$
- 기존의 MC는 state별로 return을 저장해둬야 되지만 이 방법을 통해 기존의 구해둔 평균에 새로운 값이 들어오면 어느 정도의 비율로 보정을 해주면 됨.(즉 새로운걸 얼마나 받아 들이고 과거를 얼마나 잊을지를 비율로서 결정함.)
- $\alpha$를 fix하면 non-station problem(MDP가 계속 바뀜)에서는 유용함(과거는 잊자.)
- 매번 $G_t$를 향해 조금씩 움직인다고 생각해도 좋음
Temporal-Difference
- MC와 동일하게 경험으로 부터 학습함.
- Model-Free
- Learn from Incomplete episodes, by bootstrapping (끝까지 안가봐도된다.)
- TD updates a guess towards a guess
- $R_{t+1}+\gamma V(s_{t+1})$방향으로 업데이트함. 이를 TD-target이라고함.
직관적으로 생각해보자
우선 한 스텝을 가서 리워드를 받는다 (한 스텝을 갔으니 현재 스탭은 $t+1$)
그리고 한 스텝을 더 간 상태에서 $V$를 구해서 업데이트 한다.
또 다른 예시는 내가 중앙선을 침범했는데 반대편에서 오는 트럭과 충돌할 뻔 했다고 가정하자. MC의 경우 충돌한게 아니라서 리워드를 받지 못하지만, TD의 경우 중앙선을 침범하는 state가 좋지 않다는 것을 ‘추측‘할 수 있고 이를 통해 현재 state가 나쁜 state라고 평가를 할 수 있다.
- guess($V(s_t)$) toward a guess($V(s_{t+1})$) 조금 더 정확하게 한 스텝 가보고 그걸로 업데이트 한다는게 핵심.
- 예측치로 예측치를 업데이트 하기 때문에 틀린 방향이면 완전 최악의 결과를 얻게됨.
좀 디테일 하게 알아보자.
$G_t = R_t + \gamma G_{t+1}$로 한 스텝 가서 쪼갤 수 있는데 이로 인해서 TD가 가능하다.
\[Q(s,a) = \int(R_t+\gamma Q(s',a'))p(s'\vert s,a)p(a'\vert s')ds',a' \approx \frac1N\sum\limits_{i=1}^N(R_t^{(i)}+\gamma Q(s'^{(i)},a'^{(i)}))\]복잡해 보이지만 그냥 Q함수의 정의에서 $G_t$ 를 한 스텝 가서 리워드(R)과 $\gamma G_{t+1}$로 쪼갠 것 뿐이다.
위의 approximation은 그냥 Monte-Carlo 방법을 적용한 것.
그냥 샘플($\epsilon-greedy$로 뽑은 next state의 Q값)을 N번 뽑아서 N으로 나누자.
참고로 ‘ = 다음 타임스텝이라는 뜻
$Q_N= \frac1N\sum\limits_{i=1}^N(R_t^{(i)}+\gamma Q(s’^{(i)},a’^{(i)}))$ 이니까… $N-1$개 까지의 평균과 N 번째 샘플의 합으로 분리하면,
\[\frac1N(Q_{N-1}(N-1) + R_t^{(N)}+\gamma Q(s_{t+1}^{(N)},a_{t+1}^{(N)})-Q_{N-1})\] \[= Q_{N-1} +\frac1N(R_t^{(N)}+\gamma Q(s_{t+1}^{(N)},a_{t+1}^{(N)})-Q_{N-1})\]N-1번째 샘플까지의 평균을 구해놓고 거기서 N 번째 샘플이 들어왔을 때 새로 평균을 구하지 말고 기존에 구해놓은 평균을 좀 재사용해서 식에 적용해보자 라는게 핵심.
SARSA가 제일 최근 스텝만 본다는게 이런 의미에서 자주 나오는 말.
가장 아래 나온 수식을 Incremental Monte-Carlo update라고도 부름.
$(R_t^{(N)}+\gamma Q(s_{t+1}^{(N)},a_{t+1}^{(N)})$ 를 TD-target이라고 부르며(최근 샘플)
$(R_t^{(N)}+\gamma Q(s_{t+1}^{(N)},a_{t+1}^{(N)})-Q_{N-1})$ 를 1-step TD-error 라고 부름.
위 수식에서 $\frac1N=\alpha$로 놔두면
\[(1-\alpha)Q_{N-1} + \alpha(R_t^{(N)}+\gamma Q(s_{t+1}^{(N)},a_{t+1}^{(N)}))\]이렇게 알파로 정리할 수 있음.
Decaying $\epsilon-greedy$를 사용하여 policy를 뽑고, Q값을 구한 다음 (샘플을 통해) Q를 업데이트 할 때 마다 policy도 같이 업데이트됨!
위와 같은 프로세스를 통해 Q도 점점 $Q^*$에 가까워 지고 optimal Q일땐 greedy를 통해 optimal policy 얻으면 된다! 위 프로세스가 Optimal로 수렴하는 것은 수학적으로 고전 알고리즘 하시는 분들이 밝혀 놓았음.
TD의 단점
Q안에 결국 Expectation이 또 들어가 있어서 MC방법과는 다르게 next Q가 완벽히 좋은 샘플이라고 할 수 없음, 즉 TD-targe은 (샘플로서)문제가 좀 있음. 기존의 MC는 pdf를 따르는 샘플, $G_t$는 또 거기에 맞는 pdf를 따른 샘플을 정확히 뽑지만 next Q는 좀 다름. next Q는 완벽하지 않음. Expectation을 통해(다 계산해서) 완벽하게 옵티멀 Q로 수렴된 상태가 아니기 때문에 업데이트 해나가는 중이었음.
즉, True TD target $R_{t+1} + \gamma v_\pi(S_{t+1})$는 $v_\pi(S_t)$에 대한 unbiased estimate 이지만, 실제론 $v_\pi(S_t)$를 알려줄 신이 없으므로 $R_{t+1} + \gamma V(S_{t+1})$ 로 업데이트 하게 되고 이는 biased estimate 임
그로 인해 bias가 생김. Expectaion 안의 Expectation이기 때문!
MC vs TD
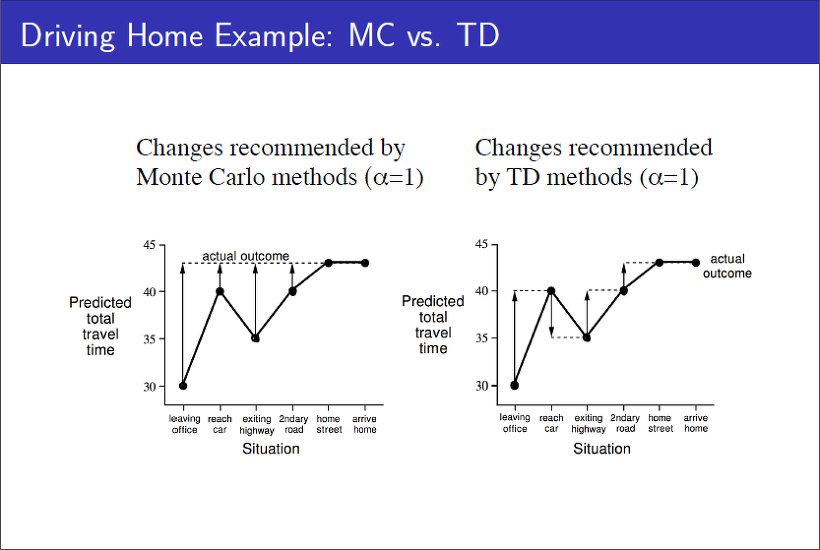
위 그림에서 나타나는 화살표가 각각의 state에서 update 대상이 되는 즉 step size($\alpha$)에 곱해지는 Error이다.
MC의 경우 에피소드가 모두 끝나야 업데이트를 할 수 있는 도구가 생기는데, MC의 도구는 지나온 state마다 reward를 통해 계산한 return $G_t$ 이다.
반면에 TD의 경우 매 스텝 마다 얻은 reward를 통해 업데이트를 진행한다. 각각의 state에서 마주하는 상황들을 비교해가면서 업데이트하므로 화살표의 방향이 바뀌는 것을 볼 수 있다.
MC는 자명하게도 Unbiased high Variance이고,
TD는 모델로 부터 실제 얻는 정보는 다음 스텝의 reward + $V(s_{t+1})$ 인데, 심지어 이 $V$도 추정 값이므로 bias가 매우 높다.(TD의 단점에서 언급한 기댓값의 기댓값 형태)
Bias-Variance Trade-off는 딥러닝을 포함한 강화학습에서도 자주 다뤄지는 친구인데, 이 두 녀석을 줄이기 위해 나온 방법들이 존재한다.
N-step TD, TD($\lambda$)

위 슬라이드를 보면 알겠지만 N의 크기를 에피소드가 끝날 때 까지라고 한다면 N-step TD는 MC와 같아진다.
그런데.. N-step TD가 좋은 건 알겠는데 N을 어떻게 구할 수 있을까?
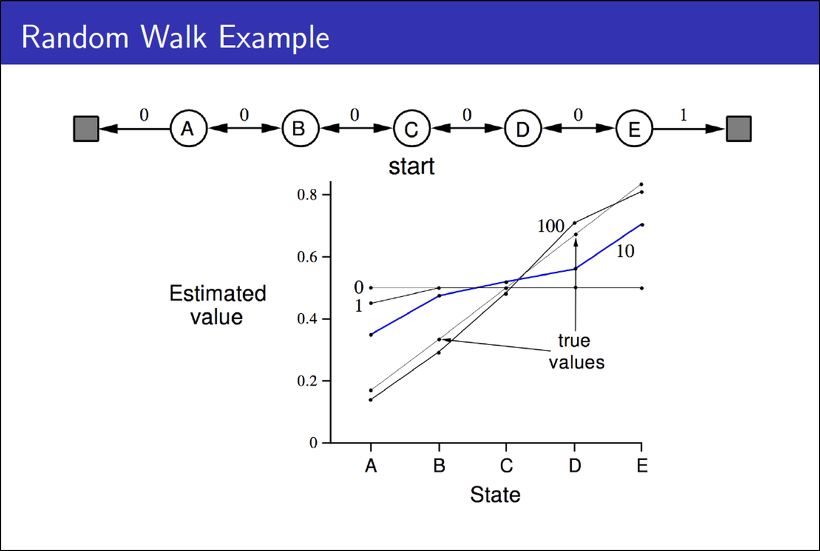
state ‘C’에서 시작해 양 끝에 있는 terminal에 도착하는 양방향의 액션이 존재하는 문제이다. C에서 시작해서 랜덤 액션을 취해 얻은 정보를 바탕으로 true value func.을 prediction 3해야 한다.
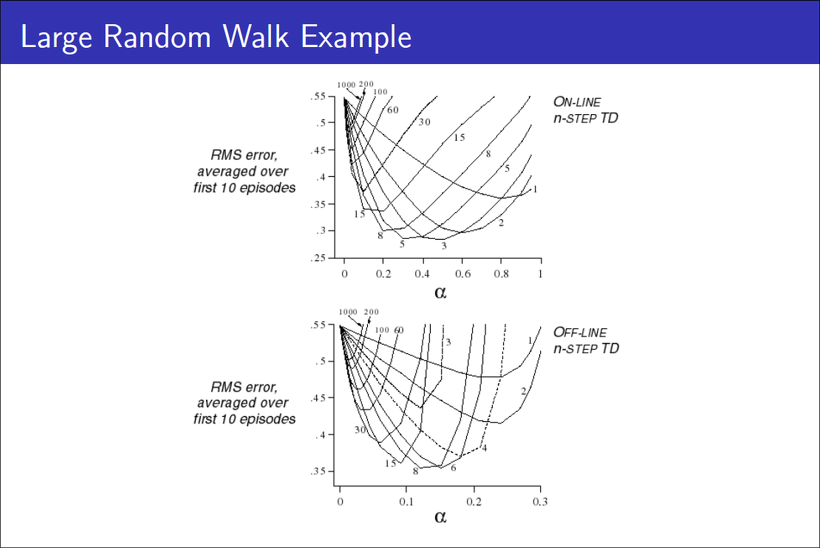
위 그래프를 통해 보면 알 수 있듯, MC-TD의 장점이 N-step이라면, N-step사이에서 평균을 구하는 것도 해답이 될 수 있을 것 같다.
그러나 여기선 단순 평균을 취하지 않고 $\lambda$라는 파라미터를 통해 geometrically weighted average를 취한다. N-step마다 얻어진 return에다 이 파라미터를 곱해 $\lambda$-return($G_t^{\lambda}$)를 만들고 이 return으로 업데이트를 진행한다.
최종 수식은 다음과 같다.
$V(S_t)\leftarrow V(S_t) + \alpha(G_t^{\lambda}-V(S_t))$
$G_t^{\lambda} = (1-\lambda)\sum\limits_{n=1}^{\infty}\lambda^{n-1}G_t^{(n)}$
대충 1-step TD에는 (1-$\lambda$), 2-step에는 (1-$\lambda$)$\lambda$, 3-step에는 (1-$\lambda$)$\lambda^2$ 이런식으로 전개된다고 보면 될 것 같다.
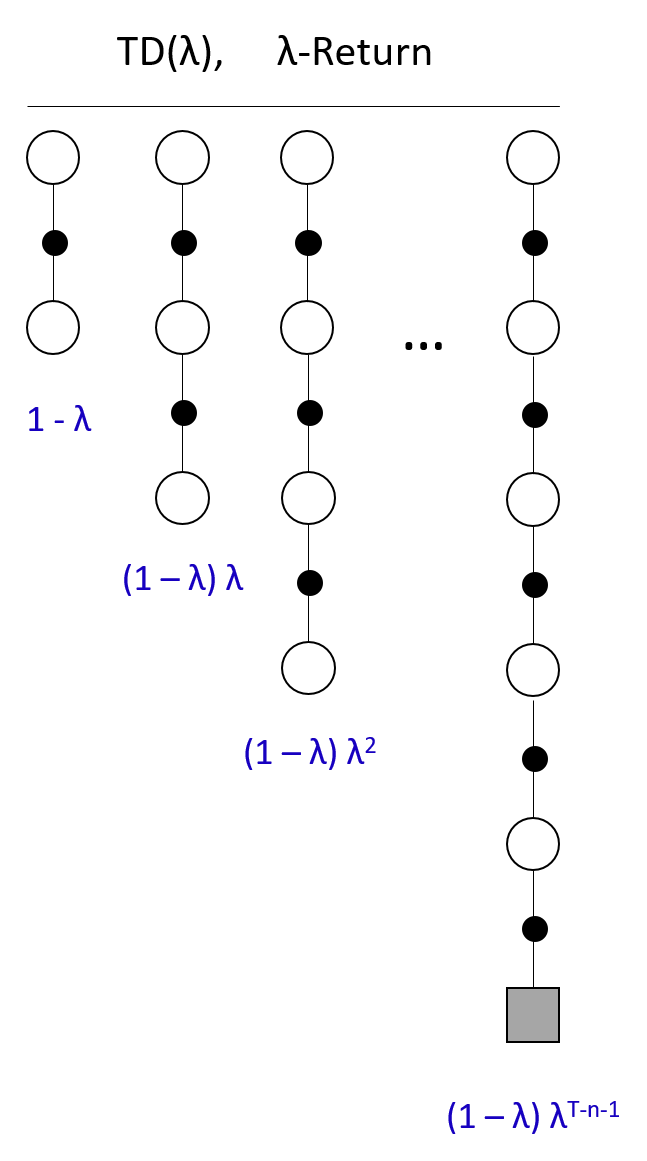

Comments