L1, L2?
15 Sep 2020 | Loss요즘 비전 관련 구현만 하다보니 ML기본 이론을 볼 일이 딱히 없었는데, 톡방에서 아주 기본적인 질문을 받았습니다. RSS에서 제곱을 사용하는 이유가 뭔가요?
아는내용은 좀 있지만 정리가 되질 않아서 정리해 봤습니다.(아직 아래에 L1 L2 norm이 Lasso, ridge회귀에서 사용되는 부분에 대한 정리가 부족합니다 ㅜ)
일단 위키에 따르면
In regression analysis, the term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom.
라고 합니다.
그러니까 우선 헷갈리는 RSS, L2loss, MSE를 모두 수식으로 나타내 봅시다.
\[RSS=\sum\limits_{i=1}^n(y_i-t_i)^2\] \[L2\:Loss = \sum\limits_{i=1}^n(y_i-t_i)^2\] \[MSE = \frac1n \sum\limits_{i=1}^n(y_i-t_i)^2\]RSS는 수식으로 보면 L2 Loss(Least square error)와 같고, MSE는 위키에 나온 대로 RSS에서 자유도를 나눠준 값임을 알 수 있습니다.
사실 톡방에서 나온 질문은 분산이 왜 편차의 제곱인가요? 라는 질문과 같습니다.
일단 편차의 합은 0이므로, 저걸 상쇄해줘야 한다는건 직관적으로 와닿습니다. 그렇다면 음수값을 없애는 절댓값을 취하면 어떻게 될까요?
\[L1\:loss = \sum\limits_{i=1}^n\vert y_i-t_i\vert\]이렇게 L1 loss로 표현됩니다. 그러나 우리는 절댓값의 경우 non differentiable한 경우가 있습니다. 미분 적분이 귀찮아 진다는 얘기죠? 그래서 제곱을 사용하면 기존의 저희가 알던 분산식과 똑같은 L2 Loss가 나오게 됩니다.
L1 loss & L2 loss
이왕 이 둘을 알게된 김에 이 둘의 특징을 비교해봅시다.
-
L2는 제곱을 가지고 있기 때문에 직관적으로 outlier에 민감합니다. 즉 L1 loss가 더 Robust합니다.
-
기존의 데이터와 비교적 비슷한 새로운 데이터가 들어왔을 때 L2가 조금 더 stable한 예측을 할 수 있다고 합니다.(즉 기존 데이터에 대해서 비슷한 데이터가 들어올 경우 L1이 조금 더 잘 움직이고, Outlier인 경우 L2가 더 극단적이다.)
L1과 L2는 Regularization으로도 활용 됩니다.
L1 Regularization
\[Cost(w,b) = \frac1m \sum\limits_{i=1}^nL(\hat y_i,y_i) + \lambda \frac12\vert w\vert\]L2 Regularization
\[Cost(w,b) = \frac1m\sum\limits_{i=1}^nL(\hat y_i,y_i)+\lambda\frac12\vert w\vert^2\]여기서 $\vert w\vert$ 는 norm 이며, 민코프스키 거리에서 차원이 1일때, 2일때가 각각 L1 norm, L2 norm 입니다. norm의 계산 결과로 나온 수치는 원점에서 벡터 좌표 까지의 거리이며 magnitude라고 부릅니다.
\[d(A,B) = [\sum\limits_{i=1}^p(x_i-y_i)^m]^{\frac1m}\]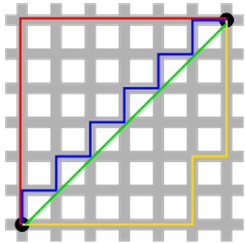
엄청 많이봤을 그림입니다.
위에 녹색선이 L2 loss이며 2차원 상에서 최단거리를 나타냅니다.(따라서 계산에서 좀 더 효율적)
Why L1 norm for sparse models?
L1, L2에 대해 공부하다보면 L1이 sparse하다는 설명을 보게 됩니다. 왜그런걸까요?
2차원 벡터 $\mathbf x = (1,\epsilon)$를 고려해봅시다 단, $\epsilon>0$
벡터의 L1 norm은 $1+\epsilon$, L2 norm은 $1+\epsilon^2$ 입니다.
이제 정규화 절차의 일부로, $\mathbf x$의 요소 중 하나의 크기를 $\delta\leq \epsilon$ 만큼 줄여봅시다. (즉 $x_1 = 1-\delta$)
\(\vert\vert \mathbf x-(\delta,0)\vert\vert_1 = 1-\delta +\epsilon\)
\[\vert\vert \mathbf x-(\delta,0)\vert\vert_2^2 = 1-2\delta+\delta^2 +\epsilon^2\]반면에 $x_2$를 $\delta$ 만큼 줄이면 다음과 같습니다.
\[\vert\vert \mathbf x-(\delta,0)\vert\vert_1 = 1-\delta +\epsilon\] \[\vert\vert \mathbf x-(\delta,0)\vert\vert_1 = 1-2\epsilon\delta +\delta^2+\epsilon^2\]여기서 주목할 점은 L2 norm에 대하여 더 큰 항 $x_1$을 정규화 하면 더 작은 항 $x_2$에 정규화하는 것 보다 더 큰 감소를 가져옵니다.(하지만 L1 norm은 똑같죠?)
이해안가면 (5,1)에서 (4,1)을 만들었을 때 (5,0)를 만들었을 때 각각의 L1, L2norm을 구해보세요.
직관적으로 생각하면 반지름의 길이가 5인 원을 기준으로 (4,1)은 원 안에 존재하고, 5,0은 원의 둘레 위에 존재합니다 각 점에서 원점까지의 거리가 L2norm이니까 무슨말을 하고싶은지 감이 오시나요?
L1 norm이 sparse를 유도한다기 보다는 L2 norm이 어떤 의미에서 요소가 0에 가까워짐에 따라 감소하는 부분을 억제한다고 볼 수 있습니다.
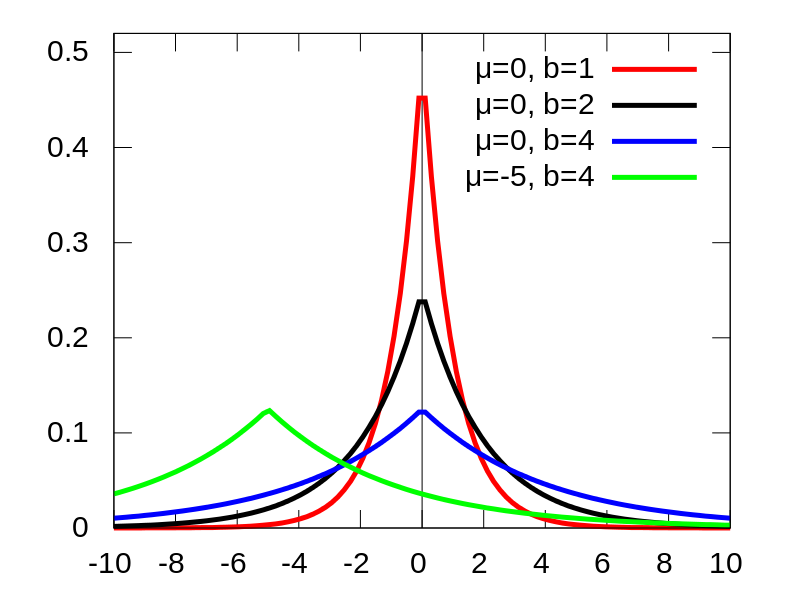
또한 Lasso의 경우 베이지안관점에서 베타의 사전분포로 다음과 같은 더블 익스포넨셜 분포를 따릅니다.(뭔가 있어보이죠?)
사실 정규분포랑 비슷하긴한데 0으로 조금 더 날카롭게 몰린 형태의 분포입니다.
이 분포를 봐도 기존의 베타(ML에서는 Weight인 w)가 0을 선택하려는 경향이 강함을 알 수 있습니다.(이는 위에서 전개한 수식과 동일한 의미인데 다른 표현 방식입니다.)
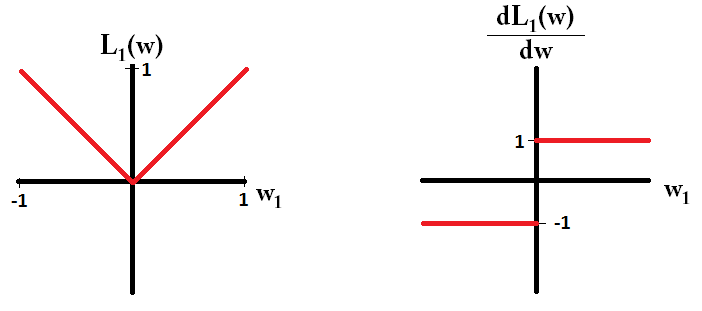
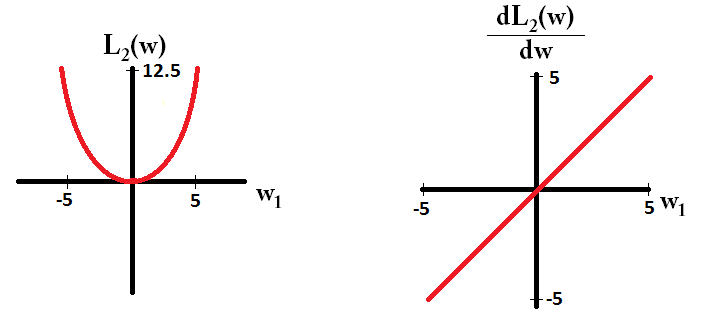
또한 gradient 개념으로 들어가도 설명이 가능한데, 아래의 그림을 보면 알겠지만 L1 gradient는 항상 일정 크기(1)만큼이 곱해지므로 빠르게 0에 가까워집니다.
그러나 반대로 L2의 경우 L1에 비해 0에 가까우려면 굉장히 많은 스텝을 거쳐야 합니다.

Comments