왜 분류에서는 CrossEntropy를 사용할까?

04 Sep 2020 | Loss

회귀문제에선 MSE, 분류문제에선 CE를 씁니다.

왜 그런지 생각해보신적 있으신가요? 사실 MSE를 회귀문제에서 사용하는 것은 꽤나 직관적입니다.

오늘은 왜 MSE가 아닌 CrossEntropy를 분류문제의 loss function으로 사용하는지 알아봅시다.

CrossEntropy?

예전 제 블로그 포스팅에서 MLE를통해 가장 likelihood가 높은 파라미터를 추정하는 것이 사실상 KLD를 최소화하는 문제와 동일하며, KLD를 최소화 하는 문제가 바로 CrossEntropy를 최소화 하는 문제가 된다고 말씀 드렸습니다.

그렇다면 “MLE를 하는 것이 CrossEntropy loss를 최소화 하는 것과 동일하다.” 라는 전제를 깔고 시작해봅시다.

우선 MSE와 CE를 비교하기에 앞서 왜 CE를 최소화 하는 것이 MLE와 같고, 수식전개가 들어간 포스팅에선 한번씩 들어봤을 Negative-log likelihood를 최소화 하는 것과 같은지 알아봅시다.

여담이지만 저는 왜 이렇게 CrossEntropy 수식이 외워지지 않을까요..

Likelihood는 다음과 같이 정의합니다.

\[\cal L(\theta\vert x_1,...,x_n) = f(x1,...,x_n\vert \theta) = \prod\limits_{i=1}^nf(x_i\vert\theta)\]

여기서 한 가지 트릭을 사용하는데요 바로 양변에 로그를 취합니다.

로그 변환에는 여러가지 장점이 있습니다.

  • 확률은 0~1사이의 값입니다. 이걸 계속 곱해줄 경우 언더플로우가 발생할 수 있는데 log를 취하면 곱하기 연산이 더하기 연산으로 바뀌므로 이를 예방할 수 있습니다.
  • 곱으로 표현된 수식을 더하기로 분리할 수 있습니다.(뭐 나중에 미분하거나 할 때 곱으로 연결된 수식을 덧셈으로 분리하면 편하겠죠…?)
\[log\: \cal L(\theta\vert x_1,...,x_n) =\log\sum\limits_{i=1}^nf(x_i\vert\theta)\]

MLE를 통해 추정한 파라미터를 $\hat \theta $라고 하면 식은 다음과 같습니다.

\[\hat \theta = argmax \sum\limits_{i=1}^n log\:f(x_i\vert\theta)\]

위 식은 다음과 같이 바뀔 수 있습니다.

\[\hat \theta = argmin -\sum\limits_{i=1}^n log\:f(x_i\vert\theta)\]

따란~ MLE가 사실은 negative-log likelihood를 최소화 하는 것과 같았네요?(사실 이건 당연한 얘기입니다.)

그렇다면 다시 CrossEntropy 식으로 돌아와서 우리가 최소화 하려고 하는 식은 다음과 같습니다.

\[H(P,Q) = -\sum P(x)log Q(x)\]

여기서 오른쪽 $Q(x)$가 모델에 대한 분포 부분이니 파라미터 $\theta$를 통해 likelihood로 나타낼 수 있습니다.

\[H(P,Q) = -\sum P(x)log Q(x;\theta)\]

위 식을 최소화 하는 것은 “데이터 분포 $P(x)$와 가장 유사한 $Q(x)$의 분포를 만드는 파라미터 $\theta$를 찾아라” 가 됩니다. 사실상 했던 얘기지만 KLD랑 다를게 없습니다.

정리해봅시다. Cross Entropy를 최소화 하는 것은 모델의 분포를 데이터의 분포와 비슷하게 만드는 것이고 이는 KLD를 최소화 하는 것과 같으며, 궁극적으론 MLE를 수행하는 것과 같습니다. 따라서 negative-log likelihood를 사용하는 것은 매우매우 합리적입니다.

그러므로 다음과 같은 문장이 성립합니다.

“Maximum likelihood estimation is equivalent to minimizing negative log likelihood.”

우리가 앞서 설정한 전제와 동일하죠?

여담이지만 Negative-log likelihood의 몇 가지 장점이 있다고 합니다.(Ratsgo 님 블로그 참조)

loss function으로 사용할 경우 우리가 만드는 모델에 다양한 확률 분포를 가정할 수 있어서 유연하게 대처할 수 있다고 합니다. Negative-log likelihood로 정의한 CrossEntropy는 비교 대상의 확률 분포의 종류를 특정하지 않기 때문입니다.

또한 앞선 포스팅해서 언급했듯 데이터가 정규분포를 따를 때 MSE와 CrossEntropy는 동치입니다.

한편 딥러닝 모델의 최종 출력을 어떤 숫자 하나(예컨대 영화 관객 수)로 둘 경우 우리가 구축하려는 모델이 정규분포라고 가정하는 것과 깊은 관련을 맺고 있습니다. 최종 출력이 O, X로 이뤄진 이진변수(binary variable)일 경우 모델을 베르누이 분포로 가정하는 것과 사실상 유사합니다. 다범주 분류를 하는 딥러닝 모델은 다항분포를 가정하는 것과 비슷합니다.

위 세 종류 모델의 최종 output node는 각각 Linear unit, Sigmoid unit, Softmax unit이 되며, output node의 출력 분포와 우리가 가진 데이터의 분포 사이의 차이가 곧 크로스 엔트로피가 됩니다. 이 차이만큼을 loss로 보고 이 loss에 대한 그래디언트를 구해 이를 역전파하는 과정이 딥러닝의 학습이 되겠습니다. 바꿔 말하면 각각의 확률분포에 맞는 손실을 따로 정의할 필요가 없이 음의 로그우도만 써도 되고, output node의 종류만 바꾸면 세 개의 확률분포에 대응할 수 있게 된다는 이야기입니다. 매우 편리한 점이죠.

MSE vs CE

CE에 대해 자세히 알아봤으니 어느정도 자신감이 생겼으리라 믿습니다.

그렇다면 classification 문제에서 MSE대신 CE를 사용하는 이유가 무엇일까요?

예제를 통해 알아봅시다.

Softmax를 통해 나온 아웃풋(확률)과 레이블 그리고 정답 유무에 대한 두 가지 케이스가 있습니다.

Output         | Label   | correct
----------------------------------
0.3  0.3  0.4  | 0  0  1 | yes
0.3  0.4  0.3  | 0  1  0 | yes
0.1  0.2  0.7  | 1  0  0 | no 

Output         | Label   | correct
----------------------------------
0.1  0.2  0.7  | 0  0  1 | yes
0.1  0.7  0.2  | 0  1  0 | yes
0.3  0.4  0.3  | 1  0  0 | no

두 가지 케이스 모두 정확도는 66%입니다 하지만 전자의 경우 확률이 굉장히 높게 나온 케이스에 대해서도 예측을 잘 하지 못했습니다. (0.7의 확률로 2번째 인덱스가 정답인데 오답을 뱉었죠?)

이런 경우 같은 정확도여도 후자가 더 낫다고 합리적으로 말하고 싶습니다. 그런데 그렇게 말 할만한 근거가 부족합니다. 어떻게 해결해야 할까요?

CrossEntropy Loss를 도입해서 Loss를 수치화 해봅시다.

첫 번째 경우는 다음과 같습니다.(단순히 CE연산이 아니라 평균입니다.)

-(ln(0.4) + ln(0.4) + ln(0.1)) / 3 = 1.38

두 번째는 다음과 같습니다.

-(ln(0.7) + ln(0.7) + ln(0.3)) / 3 = 0.64

두 번째 경우가 loss가 더 낮습니다.

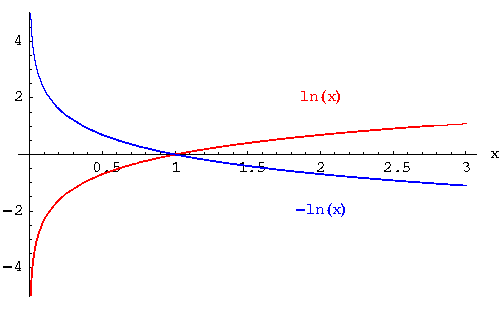
CE Loss는 우리가 들었던 예시처럼 누가봐도 정답인데 오답을 뱉어낼 경우 더 큰 Loss를 얻게 됩니다. 첫 번째 식에서 0.1이라는 작은 확률을 정답으로 예측 했을 때의 패널티가 $-ln(0.1)$이니까 굉장히 큰 패널티겠죠?

그렇다면 MSE를 통해서 두 가지 경우에 대한 Loss를 측정하면 어떻게 될까요?

첫 번째 경우는 다음과 같습니다.

(0.54 + 0.54 + 1.34) / 3 = 0.81

두 번째 경우는 다음과 같습니다.

(0.14 + 0.14 + 0.74) / 3 = 0.34

사실 MSE도 결과만 놓고 보면 꽤나 괜찮지만, 실제로 틀린 경우에 대한 패널티가 너무 큽니다.

위의 0.1의 확률을 1(정답)이라고 한 경우의 MSE는 $(1-0.1)^2$을 통해 굉장히 높은 패널티를 부여하게 됩니다.

그리고 또 하나의 문제점은 역전파 시에 발생합니다.

output은 0~1사이 값이고 역전파 시에 output*(1-output)이 계속해서 지속된다면 gradient vanshing이 생길 수도 있습니다.

이 부분이 좀 애매할 수 있는데… logistic regression이라서 아웃풋이 Sigmoid이고 그것에 대한 미분을 하게 되면 $\sigma(x)’ = \sigma(x)*(1-\sigma(x))$ 라서 위처럼 gradient가 점점 작아질 수 있다는 건 납득이 갑니다.

그리고 CE Loss에 대하여 $\frac{\partial L}{\partial x} = \sigma(x) - label$ 이고, 한 번 더 미분한 Hessian은 위처럼 $\sigma(x)’ = \sigma(x)*(1-\sigma(x))$ 값이 나오므로 $0\leq\sigma(x)\leq1$이기 때문에 항상 양수라서 Convex보장되는 CE Loss가 더 좋다고 말할 수도 있을 것 같습니다.

그러나…

Softmax의 경우 Convex가 보장되는가?

그래서 CE Loss가 MSE보다 좋다고 말할 수 있는가? 는 잘 모르겠습니다.. 혹시 아시는분 계시면 댓글 달아주세요!

이건 앞서 말했듯 CE를 사용할 경우 Negative-log likelihood이기 때문에 깔끔하게 사라집니다.

Reference

Ratsgo

Why you Should Use Cross-Entropy Error

Related Posts

Comments