PCA

일반적인 다변수 회귀 식을 적어 봅시다.

데이터가 $n$개 있을 때 식을 행렬 형태로 표현하면 다음과 같습니다.

Linear System의 두 가지 풀이 방법이 있습니다.

1. $Ax = b \rightarrow x = A^{-1}b$ (역행렬을 이용한 풀이)
2. Eigen transformation을 이용한 좌표 축의 재 설정

여기서 우리는 2번의 풀이를 살펴보겠습니다.

고유 값과 고유 벡터

선대를 수강했다면 익숙한 친구들입니다. 고유값과 고유벡터가 뭔지 우선 알아봅시다.

어떤 벡터에 행렬을 곱하면 벡터에도 변화가 일어납니다. 보통 우리는 직관적인 이해를 위해 행렬을 곱해서 모양이 변형된다(선형 변환)라고도 표현하는데요, 다음의 그림이 굉장히 직관적입니다.

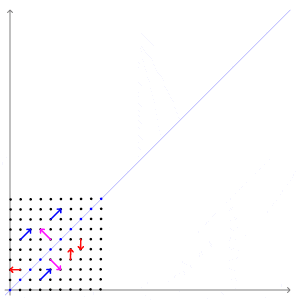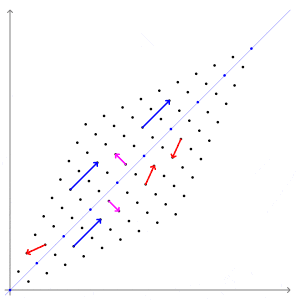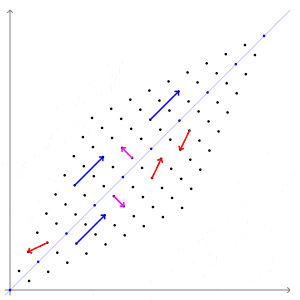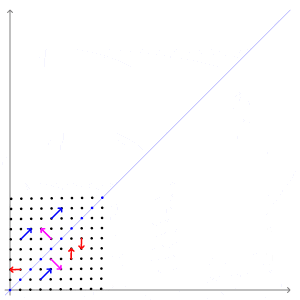
자세히 살펴 보시면 특정 벡터(파란 벡터)는 방향이 변하지 않고 크기만 변하게 됩니다.

파란 벡터는 선형 변형이 진행되는 방향와 동일하기 때문에 방향이 변하지 않습니다.

크기만 변한다는 의미는 벡터에 스칼라를 곱한 $\lambda x$로 똑같은 변환이 가능하다는 의미입니다.

그래서 위 식의 직관적인 의미는 “선형 변환을 했을 때 방향이 보존되고 값만 변하는 벡터가 존재한다” 이고, 그 벡터가 고유벡터입니다.

다시 우리의 회귀분석으로 돌아가봅시다.

우리가 가지고 있는 $X_1,X_2,X_3,…$와 같은 벡터들을 통해 예측값 $Y’$를 만들어 냈고 잘 만든 식인 경우 이 $Y’$은 벡터들로 표현 불가능한 $\epsilon$(아래 그림에서 빨간 벡터)과 수직일 것입니다.(orthogonal)

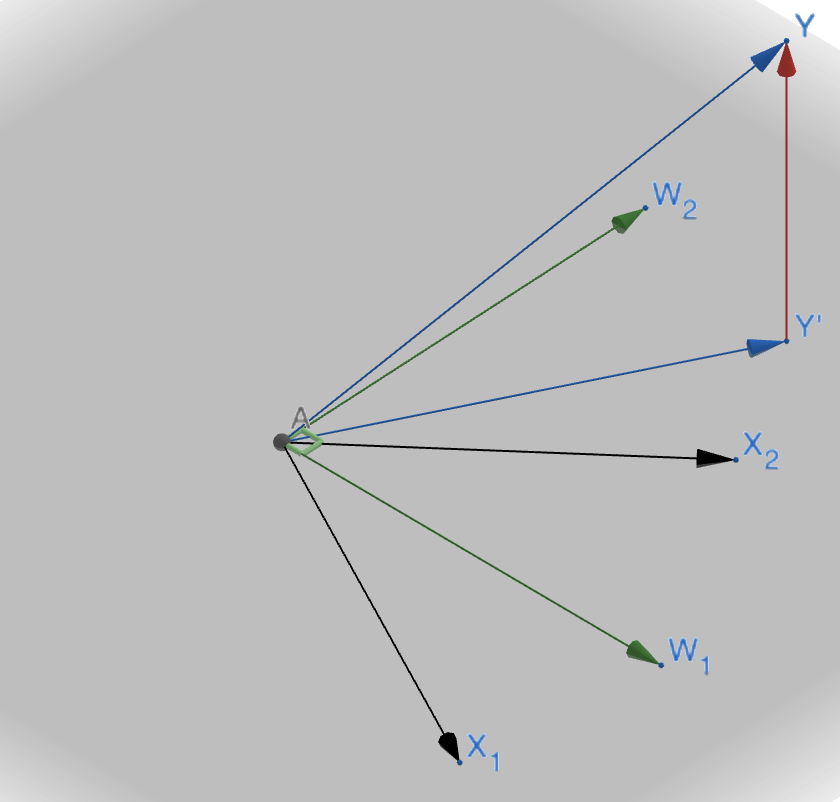
$X_1,X_2,W_1,W_2$는 모두 같은 평면위에 존재합니다. 이 말 뜻은 $(X_1,X_2)$가 만드는 공간과 $(W_1,W_2)$가 만드는 공간이 같다는 얘기입니다.

그런데, $(W_1,W_2)$는 직교합니다. 마치 저희가 배운 좌표평면의 축과 같습니다. 이를 통해서 $Y’$벡터를 나타내는 것이 $(X_1,X_2)$를 통해 나타내는 것 보다 조금 더 편리합니다.

그렇다면 기존의 벡터와 서로 같은 공간을 만들면서 직교하는 벡터는 어떻게 찾을 수 있을까요?

이게 바로 위에서 언급한 Eigen transformation입니다. 즉 다시말해서 위의 $(W_1,W_2)$는 eigen vector 입니다.

Principal Component Analysis

그렇다면 다시 회귀 분석으로 돌아와봅시다.

우리의 종속 변수 $Y$가 기말고사 성적이고 나머지는 성적을 예측하기위한 변수들이라고 생각해봅시다.

위 식에서 $X_k (1\leq k\leq m)$가 중간고사 성적입니다.

그런데 모든 학생들이 오픈북으로 중간고사를 쳐서 100점을 맞았다고 합시다.

이런 상황에서 $X_k$는 종속변수 $Y$를 설명할 때 의미가 없는 변수가 되버립니다. 직관적으로 학생마다 성적이 다양할 수록 $Y$를 더 잘 설명하기 쉽습니다. 그래야 유의미한 상관관계를 포착할 수 있을테니까요. 여기서 우리는 한 가지 힌트를 발견할 수 있는데 변수의 분산이 종속 변수를 설명하는데 중요한 요인이라는 것입니다.

좀 직관적으로 설명해봅시다. 2차원에 데이터가 흩뿌려져 있을 때 그 데이터를 가장 잘 표현하는 축 2가지를 찾는 문제입니다.

첫 번째로는 가장 분산이 큰 쪽을 축으로 하고 그 축의 직각에 있는 다른 축을 선택할 수 있습니다.

이게 바로 2차원에서 PCA의 예시입니다.

각 변수간의 분산 즉, 공분산을 행렬로 나타내봅시다.

이런식으로 행렬의 대각 성분은 각 변수의 분산이고 나머지는 공분산을 나타내는 행렬을 Covariance Matrix 라고 합니다.

위 행렬은 간단하게 다음과 같은 형태로 나타낼 수 있습니다.

그렇다면 변수와 종속 변수 간의 공분산은 다음과 같이 나타낼 수 있습니다.

흔히들 말하는 상관 계수도 공분산의 scale을 조정해준 식일 뿐입니다.

Cov Matrix를 앞서 배운 Eigen Decomposition으로 쪼갠 다음 Eigen value값 순서대로 Eigen vector들을 나열하면 어떻게 될까요?

기존의 $X_1,X_2,…,X_m$이던 벡터를 Eigen vector $Z_1,Z_2,…,Z_m$으로 나타낼 수 있습니다. 즉, Eigen vector가 주성분 벡터가 됩니다.

이 때 벡터 $Z$는 기존 데이터를 표현할 때 많이 쓰일 수록 Eigen Value값이 큽니다.(즉, 분산의 크기가 큰 경우 Eigen Value가 큽니다.)

Related work

위의 내용이 일반적인 PCA에서 다루는 내용입니다.

쓰임새를 좀 더 찾던 와중 재밌는 예시가 몇 개 있어서 가져왔습니다.

출처 : 다크프로그래머

PCA를 하게 되면 가장 첫 번째 주성분(Eigen vector)는 그 데이터의 분산이 가장 심한 방향을 나타냅니다. 이것에 대한 직관적인 설명은 사실 우리가 일반적으로 데이터의 분포가 있고 그 분포를 가장 잘 설명해주는 회귀 선을 찾는 문제를 생각해보면 회귀선과 첫 번째 주성분이 직관적으로 같은 방향임을 알 수 있습니다. 즉, 분산이 가장 큰 방향은 그 데이터를 가장 잘 표현해주는 선을 찾는 것입니다.

그래서 위의 사진을 보면 얼굴에 대한 PCA를 수행했을 때 첫 번째 주성분은 공통적으로 사람이 가지고 있는 얼굴에 존재하는 정보를 담고 있고, 뒤로 갈수록 eigen vector의 조합들로 설명 불가능한(저기 위의 3차원 벡터 좌표계 그림에서 $\epsilon$)과 같은 noise를 포함한다고 해석하면 됩니다.

또 다른 예시입니다.

공분산 행렬의 고유 벡터가 데이터 분포의 분산 방향이 되고, 고유값이 분산의 크기라고 해석 가능한 이유는 제가 위에서 앞서 시험성적의 데이터 회귀 분석을 통한 예시로 설명드렸습니다.

이걸 직관이 아닌 수식으로 표현해봅시다.

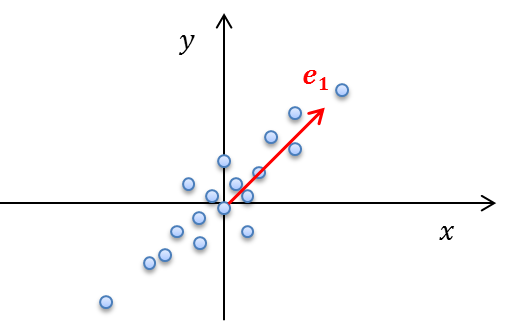
바로 위의 그림에서 $e_1$을 eigen vector라고 생각해보고 위의 데이터에 대해 왜 분산이 가장 크게 만드는 방향인지 살펴봅시다.

분산을 $\sigma^2$이라 놓고 기존의 데이터를 $X$라고 합시다.

$e_1$을 단위벡터라고 생각하고 ($e_1^Te_1 = 1$)를 만족하면서, 위 값을 최대로 만드는 eigen vector $e_1$을 찾는 문제로 생각 할 수 있습니다. $\lambda$를 써서 최적화 문제로 바꾸면 아래와 같습니다.

늘 사용했던 양변을 $e_1$에 대해 미분해서 0으로 만드는 값이 u를 최대로 만드는 값이겠죠?

따라서 위 식은 저희에게 익숙한 $Ax = \lambda x$와 동일한 것을 알 수 있습니다.

즉 데이터 $X$에 대한 공분산 행렬 Cov의 eigen vector가 분산(고유값)을 최대로 하는 방향 벡터임을 알 수 있습니다.

또한 엔트로피로도 PCA를 설명 가능한데 데이터의 분포를 주성분을 통해 나타내면 성분의 차수가 낮아질수록 분산이 감소합니다.(이건 이제 직관적으로 와닿으시죠? 분산이 높을수록 자주 사용되는(공통의) 정보를 표현하기 위함이니 앞쪽의 주성분일 수록 분산이 클테니까요.)

그리고 분산이 낮아진다는 것은 엔트로피가 감소하는 것을 의미합니다. 즉, PCA의 첫 번째 주성분이 가장 엔트로피를 감소시키는 차원을 고르는 것과 같습니다.

Reference

다크프로그래머

Data Science Today