parameter estimation in ML
31 Aug 2020 | statisticsMLE, MSE, OLS, KLD 등등 머신러닝 문제를 풀기 위해서 적용하는 여러가지 추정 방법이 있는데 이 추정 방법들의 연관성을 느끼고 정리했습니다.
프레임 워크를 사용해 모델을 돌려서 acc를 높이고, loss를 낮추기 위해 파라미터 튜닝과 방법론만 생각하면서 코딩만 하다 보면 그 속에 들어간 수학적 개념을 종종 잊고 지내는 것 같습니다.

엔지니어라면 자기가 돌리는 모델의 백그라운드에 들어가는 수학 정도는 이해하고 있어야겠죠?
천천히 알아봅시다.
Ordinary Least Square
OLS는 가장 기본적인 선형 회귀 방법으로 RSS(Residual sum of Squares)를 최소화 하는 가중치 벡터를 행렬 미분을 통해 구하는 방법입니다.
수식으로는 다음과 같이 나타냅니다.
\[Y = \hat Y + \epsilon\] \[Y = X\theta + \epsilon\] \[X'Y = X'X\theta +X'\epsilon\] \[(X'X)^{-1}X'Y = (X'X)^{-1}X'X\theta + (X'X)^{-1}X'\epsilon\] \[\hat \theta = (X'X)^{-1}X'Y\]일반적으로 우리의 모델이 예측한 $\hat Y$에 noise를 추가해 Y라고 나타낼 수 있습니다.
우리의 예측값은 인풋 데이터와 그에 대한 가중치를 곱한 형태로 $X\theta$처럼 나타낼 수 있습니다.
4번째 줄에서 noise term은 데이터가 커지면 0으로 수렴하므로 최적의 $\hat \theta$는 위처럼 나타낼 수 있습니다.
OLS의 특징은 데이터 분포가 정규분포를 따르면 최적의 방법이 될 수 있지만, 역행렬을 구해야 하므로 데이터가 Full rank여야 합니다.
저희가 ML을 가장 처음 배울 때 하는 linear regression(이라 쓰고 MSE 사용해서 $Y-\hat Y$ 최소화 하는 가중치를 구하는 방법)과 똑같습니다.
샘플 데이터를 가장 잘 대표하는 line 즉 , mean line을 찾는 것입니다.
Maximum Likelihood Estimation
ML에서 주로 다루는 태스크는 주어진 데이터가 있을 때 그 데이터를 잘 표현하는 모델을 설계하는 것입니다.(저는 통계전공은 아니지만 직관적으로 봐도 통계랑 관련이 굉장히 깊어 보이는 정의입니다.)
우선 MLE가 뭔지 알아보기전에 Likelihood를 정의하고 넘어가도록 합시다.
Likelihood는 가능도 라고 불립니다. (오래된 자료에선 우도라고 하는 경우도 봤습니다.) 가능도는 어떤 확률 분포로 부터 특정한 샘플 값 $x$가 발생했을 때 이 샘플 값 $x$가 나오게 하는 파라미터$(\theta)$의 확률입니다.
예를 들어 봅시다. 동전 던지기를 5번 시행했을 때 앞면이 3번 나오고 뒷면이 2번 나왔습니다.
동전 던지기는 베르누이 분포를 따르고 베르누이 분포에서 $\theta$라는 파라미터를 가지고 여기서는 앞면이 나올 확률을 $\theta$라고 하겠습니다.
‘HHHTT’ 앞면이 3번 나왔습니다 베르누이 분포에서 앞면이 나올 확률을 $\theta$라고 했는데 이러한 샘플에서 $\theta$는 누가 봐도 직관적으로 0.6이 맞는 것 같습니다.
실제로 $\theta=0.6$이 좋은 추정인지 확인해봅시다.
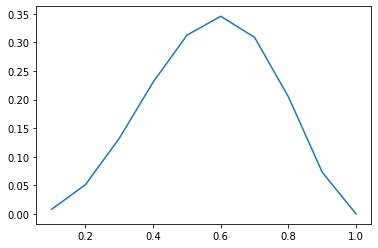
실제로 0~1 사이의 $\theta$값을 비교해봤을 때 0.6이 가장 확률이 높습니다.
‘HHHTT’ = $(0.6)^3\cdot(0.4)^2 = 0.03456$
즉, 우리가 가진 샘플 데이터 ‘HHHTT’를 가장 잘 표현하는 분포의 파라미터는 $\theta = 0.6$입니다.
사실 위의 그래프는 (0~1.0)사이의 $\theta$를 임의로 만들어서 일일이 대입해서 찾는 방식인데 좀 비효율 적입니다.
베르누이 분포를 식으로 나타 내 봅시다.
\[p(D\vert \theta) = \prod\limits_{n=1}^N p(x_n\vert \theta)= \prod\limits_{n=1}^N \theta^{x_n}(1-\theta)^{1-x_n}\]이걸 log-likelihood로 변경하고 미분해봅시다.
\[ln\: p(D\vert\theta) = \sum\limits_{n=1}^N ln\:p(x_n\vert\theta)=\sum\limits_{n=1}^N(x_nln\:\theta +(1-x_n)ln(1-\theta))\]$\sum\limits_{n=1}^Nx_n$ 은 성공횟수이므로 $N_0$로 나타내면,
\[ln\: p(D\vert\theta) = N_0ln\:\theta + (N-N_0)ln(1-\theta)=0\] \[\frac{\partial\:ln\:p(D\vert\theta)}{\partial\theta} = \frac{\partial}{\partial\theta}N_0ln\:\theta + (N-N_0)ln(1-\theta)\] \[\frac{N_0}{\theta} =\frac{N-N_0}{1-\theta}\] \[\theta = \frac{N_0}{N}\]결국 베르누이 분포에서 MLE를 통해 파라미터를 추정하는 방법은 전체 동전을 던진 횟수에서 앞면이 나온 경우를 나눈 것과 같습니다.(우리의 직관과 일치합니다!)
결론 : Likelihood를 최대로 하는 추정 방식이 MLE이다.
사실 이런 추정 방식(베르누이)은 5번 던졌을 경우 모두 다 앞면인 경우 파라미터 $\theta=1$이라고 추정해 버립니다. 일반적으론 옳지 않죠, 그래서 파라미터에 대해 사전 분포를 도입하여 해결하는 분포가 바로 이항 분포입니다.
OLS & MLE
OLS는 종속 변수가 iid 이면 Unbiased + Minmum Variance인 계수를 잘 찾아 줍니다. 장점은 분포를 몰라도 됩니다!
MLE는 iid이고, 데이터가 정규분포를 따를 때 OLS와 같은 결과를 낸다고 합니다. MLE는 분포를 알 고 있어야 풀 수 있는데, 현실에서 우리 모델의 분포와 데이터의 분포가 맞지 않는 경우가 많아서 힘들다고 합니다.
머신러닝에서 MLE를 최대화 하는 방식으로 학습 한다고 가정하고 수식으로 나타내면 다음과 같습니다.
\[\theta_{ML} = argmax\:Q(Y\vert X;\theta)\] \[=argmax\: \sum\limits_{i=1}^m log Q(y_i\vert x_i;\theta)\]MLE는 분포가 필요하니까 $Q$는 우리의 만능 키 정규분포라고 가정하겠습니다. 이렇게 정규분포로 가정하고 나면 식을 다음과 같이 바꿀 수 있습니다.
\[\sum\limits_{i=1}^m ln Q(y_i\vert x_i;\theta)\] \[= \sum\limits_{i=1}^m ln(\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}})\] \[= \sum\limits_{i=1}^m \{-ln(\sqrt{2\pi})-ln(\sigma) - \frac{(x-\mu)^2}{2\sigma^2} \}\] \[-\frac{m}{2}ln(\sqrt{2\pi}) - m\:ln(\sigma) - \sum\limits_{i=1}^m \frac{\vert\vert \hat y-y\vert\vert ^2}{2\sigma^2}\]위 식의 앞 두 항은 모두 상수에 대한 식이므로 학습중에 변하지 않고, 세 번째 항은 우리에게 익숙한 MSE와 비슷해보입니다.
따라서 정규분포를 가정하면 MLE를 통해 추정한 파라미터와 MSE를 최소화 하는 파라미터는 동일하다고 볼 수 있습니다.
KL-Divergence
ML을 공부하고 계시다면 KLD도 굉장히 익숙하실 텐데요, 수식으로 나타내보겠습니다.
\[KL(P\vert\vert Q) \simeq \frac1N \sum\limits_{n=1}^N(ln\:P(x_n)-ln\:Q(x_n\vert\theta))\]일반적으로 $P$는 데이터 분포, $Q$는 모델의 분포를 나타냅니다. 저희는 최대한 $\theta$를 잘 추정해서 $P$분포와 같도록 만드는 것이 목표입니다.
그렇다면 직관적으로 생각했을 때 샘플 데이터는 어차피 고정일테니 $Q$를 가지고 놀아야 합니다. 그런데 $Q$는 앞서 살펴본 Likelihood와 똑같이 생겼습니다. 앞서 Likelihood를 최대로 추정하는게 MLE라고 말씀 드렸죠? 그렇다면 MLE를 통해 나온 $Q$가 가장 $P$와 비슷할 테니 MLE를 통해 파라미터를 추정하는 방식과 KLD를 minimize하는게 같다고 볼 수 있습니다.
KLD & CrossEntropy
우선 우리에게 친숙한 크로스 엔트로피를 수식으로 나타내 봅시다.
\[H(P,Q)= E_{X\sim Data}[-logQ(x)] = -\sum\limits_x P(x)logQ(x)\]혹시 엔트로피를 모르신다면 여기를 참고해주세요.
또한 KLD도 다음과 같이 나타낼 수 있습니다.
\[KL(P\vert\vert Q)=H(P,Q)-H(P)\]크로스 엔트로피 기준으로 다음과 같이 정리할 수 있습니다.
\[H(P,Q) = H(P) + KL(P\vert\vert Q)\]즉, 크로스 엔트로피는 $P$에 대한 엔트로피에 $P$와 $Q$분포의 다른 정도를 더한 것으로 볼 수 있습니다. 만약 여기서 두 분포가 같다면 크로스 엔트로피 = 엔트로피가 됩니다.
우리가 분류 문제에서 사용하는 CE Loss를 최소화 하는 것은 두 분포 사이의 다른 정도인 KLD를 최소화 하는 것과 같습니다.

Comments