Planning by Dynamic Programming
10 Aug 2020 | Reinforcement LearningMDP에 대한 모든 정보를 알고 있다고 해도 최적의 policy를 구하는 것은 쉽지 않은 문제입니다.
planning은 environment에 대한 모델이(Model based) 있을 때 최적의 policy를 구하는 것을 뜻합니다.
그 방법론으로 저희 타이틀 처럼 Dynamic Programming을 사용합니다.
What is Dynamic Programming?
직관적으로 말하면, 큰 문제를 작은 문제로 나눠서 푸는 것!
작은 문제를 풀어서 솔루션들을 찾고 그 솔루션들을 모아서 큰 문제를 푸는 것입니다.
Dynamic Programming이 되기 위한 조건
- Optimal substructure
- 작은 문제로 쪼개서 각각을 최적화 해도 기존의 문제를 최적화 할 수 있다.
- Overlapping subproblems
- 작은 문제들을에 대한 결과값을 저장, 재사용 가능하다.
MDP가 위의 두 가지 조건을 모두 만족합니다.
벨만 방정식이 recursive하게 엮여 있고,
Value function이 작은 문제들의 해 -> 저장했다가 reuse 가능하다! -> Overlapping subproblems
강화학습에서 문제를 푼다는 것은 두 가지 경우로 나눌 수 있습니다.
- For Prediction
- Value function을 학습하는 것
- MDP에서 Policy가 주어졌을 value function을 계산하는 것
- For Control
- MDP가 주어졌을 때 Optimal Policy를 찾는 것
Iterative Policy Evaluation
정책이란?
에이전트가 모든 상태에서 어떻게 행동할지에 대한 정보. MDP의 목적은 가장 높은 보상을 얻게 하는 ‘정책’을 찾는 것입니다. 처음부터 이 정책을 찾을 수는 없으므로 특정 정책(e.g. random policy)을 발전시켜 나가는 방법을 사용합니다.
그렇다면 현재 정책이 좋은지 나쁜지 ‘평가’해야 하며 더 좋은 정책이 존재 한다면 ‘발전’시켜야 합니다. 정책 이터레이션에서는 평가를 정책 평가(policy evaluation)이라고 하고, 발전을 정책 발전(policy improvment)라고 합니다.
이 과정을 반복하면 정책은 최적 정책(optimal policy)로 수렴합니다.
정책 평가
정책 평가는 가치 함수를 통해 이루어집니다. 가치 함수는 현재의 정책$\pi$를 따라서 얻을 수 있는 보상에 대한 기댓값입니다.
즉, 정책의 가치는 ‘현재 정책에 따라 받을 수 있는 보상에 대한 정보’입니다.
우리는 벨만 기대 방정식을 통해 가치 함수를 재귀적인 형태로 표현할 수 있었습니다.
\[v_{k+1} = \sum\limits_{a\in A}\pi(a\vert s)(r(s,a) + \gamma v_k(s'))\]벨만 기대 방정식을 이용해서 정책을 ‘평가’ 해봅시다.
- 모든 state에 대해 V를 초기화
- $v_1 \rightarrow v_2 \rightarrow … \rightarrow v_\pi$ iterative하게 $\pi$에 수렴하도록 한다.
- Using Synchronous backups,
- At each iteration
- For all states $s\in S$
- Update $v_{k+1}(s)$ from $v_k(s’)$
이터레이션 마다 조금 더 정확한 $v_k$를 얻는 것이 목적입니다.
우리의 궁극적인 목적은 각 state에서 true value function인 $v_\pi(s)$입니다. 현재의 policy가 괜찮은지 아닌지를 판단하기 위해서 가치 함수를 사용하는데, 최초의 가치 함수는 true value function이 아닙니다. 현재 정책에 대한 각 state의 경중을 에이전트는 알 수 없기 때문에 왔다 갔다 하면서 계속 업데이트를 통해 정확한 true value function을 찾는 것입니다.
정확한 값에 도달하면 더 이상 값이 바뀌지 않는다고 합니다.
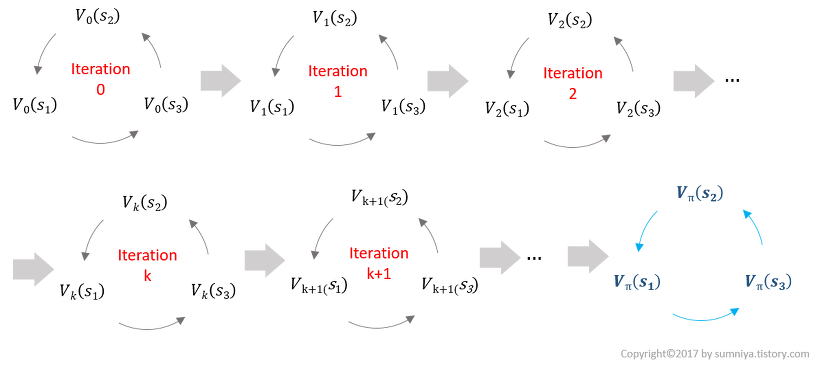
너무 추상적이니까 그림을 통해 이해해봅시다.

MDP가 있고, policy가 존재할 때 value를 찾자!
random policy를 따르고 정 사면체 모양 주사위를 던져서 방향을 결정한다고 할 때, 주사위를 평균 몇 번 던져야 검은 구역에 도착할 수 있을까요?
어려운 문제입니다. 우선 reward는 매 번 진행할 때 마다 -1을 얻을테니, reward가 최대가 되는 policy를 찾는게 이 문제를 푸는 방향일 것 같다는 생각을 할 수 있습니다.
어떻게 풀어야 할까요?
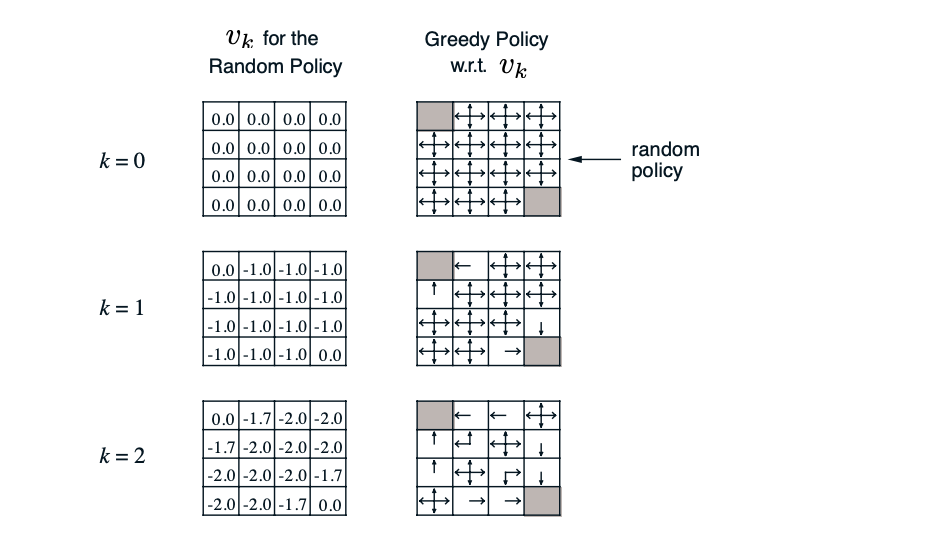
우선 $k=0$일 땐 모든 value가 0으로 초기화 됩니다.
노란색의 state를 기준으로 생각해봅시다. 여기서 나온 식은 모두 위의 벨만 기대 방정식을 그대로 사용합니다.
벽에 부딪힐 경우 자기 자신의 위치로 돌아온다고 생각하면 됩니다.
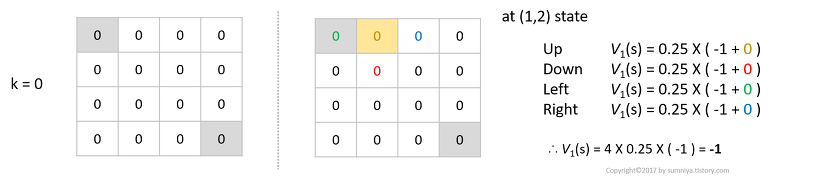
- 모든 액션에 대한 가치함수의 합은 $V_1(s)=4\times0.25\times(-1)= -1$ 입니다.
- 즉 $k=0$일 때 계산한 노란색 상태의 $k=1$에서 가치는 $-1$입니다.
$k=1$일 때는 어떻게 될까요?
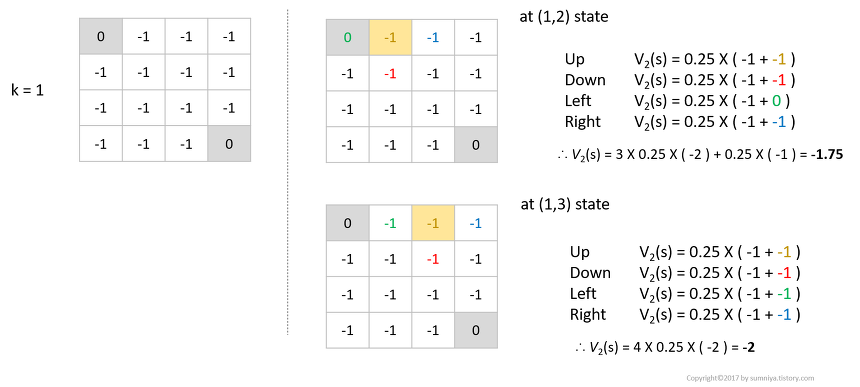
- 왼쪽으로 갈 경우는 목표지점에 도달했기 때문에 여전히 수식이 $0.25\times (-1+0)$ 이지만,
- 앞서 우리가 업데이트했던 지점들은 모두 가치가 $-1$이기 때문에 모든 액션에 대한 가치함수의 합은 $0.25\times(-1) + 3\times0.25\times(-2) = -1.75$ 입니다.
- 재밌는 사실은 (1,3)의 상태일 경우 움직일 수 있는 상태에 대한 가치가 모두 $-1$이기 때문에 (1,2)의 상태에서 가치함수 보다 더 낮은 가치함수를 얻게 됩니다.
이런 식으로 목표 지점에 도착할 경우 $G_t$에 대한 기대값이 높아지는 것을 볼 수 있습니다.
계속 업데이트하면 다음과 같은 true value function을 얻을 수 있습니다.
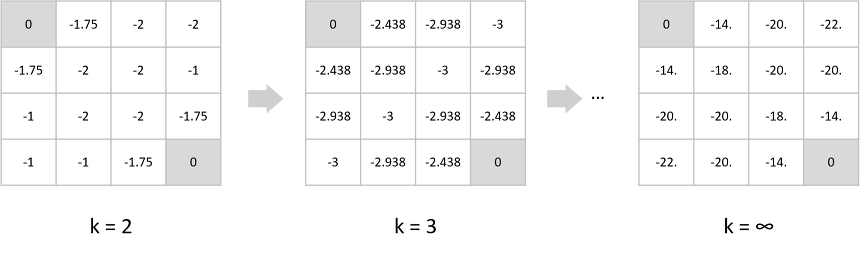
How to Improve a Policy
정책에 대한 평가를 마쳤다면 정책을 발전시켜야 합니다.
정책을 발전시키지 않는다면 정책에 대한 평가는 의미가 없습니다. 정책 발전의 방법이 정해진 것은 아니지만 여기서는 탐욕 정책 발전(greedy policy improvement)을 사용하겠습니다.
탐욕 정책 발전의 개념은 단순합니다. 정책이 모든 상태에 대한 행동을 정의한 것이기 때문에 탐욕 정책 발전도 모든 상태에 대해 적용합니다.
각 상태에 대한 정책은 랜덤 정책(0.25, 0.25, 0.25, 0.25)이었습니다. 정책 평가의 과정을 거치면서 현재 우리는 각 행동에 대한 가치를 알 수 있습니다.
정책 평가를 통해 구한 것은 에이전트가 정책을 따랐을 때 모든 상태에 대한 가치함수입니다. 그렇다면 가치함수를 통해 각 상태에서 어떤 행동을 하는 것이 좋은 지 어떻게 알 수 있을까요?
우리는 큐함수라는 액션을 포함해서 가치함수를 정의하는 방법을 배웠습니다.
\[q_{\pi}(s,a) = r_{(s,a)} + \gamma v_\pi(s')\]에이전트가 해야할 일은 이제 정해졌습니다. 각 상태$(s)$에서 선택 가능한 행동의 $q_\pi(s,a)$를 비교하고 그 중 가장 높은 큐함수를 가지는 행동을 선택하면 됩니다.(현재 상태에서 가장 가치가 높은 액션을 취하는 것! 순간 순간에 최선의 선택을 하는 것을 greedy라고 하는 것 같음)
탐욕 정책 발전을 통해 업데이트된 정책은 다음과 같습니다.
\[\pi'(s) = argmax_{a\in A}q_\pi(s,a)\]- Given a policy $\pi$
- Evaluate the policy $\pi$
- $v_\pi(s) = E[R_{t+1} \gamma v_{\pi}(S_{t+1})\vert S_t = s]$
- Improve the policy by acting greedily with respect to $v_\pi$
- $\pi’ = greedy(v_\pi)$
- Evaluate the policy $\pi$
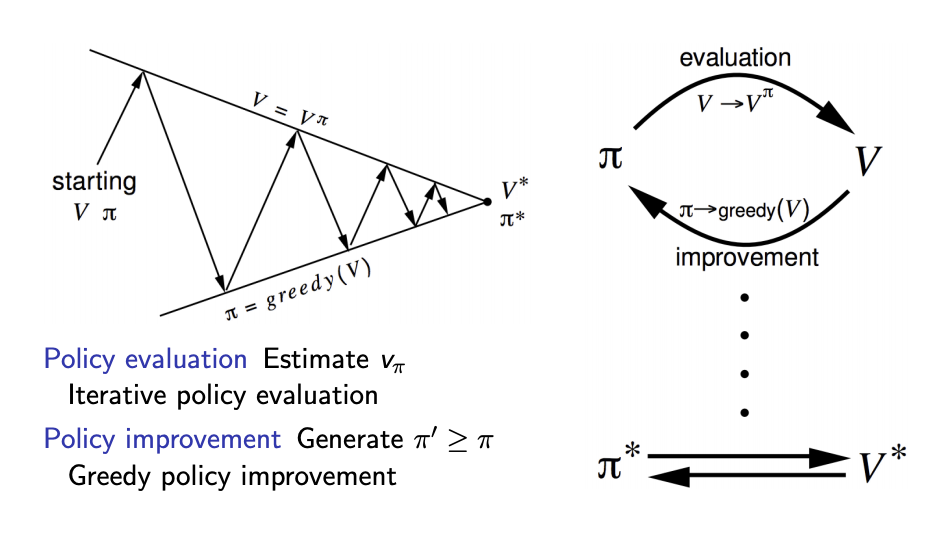
초기 가치함수 $v$, 초기 정책 $\pi$가 존재할 때 가치함수를 평가 해서 업데이트 하고, 그 위에서 greedy하게 움직이는 정책을 구합니다.
이를 반복하면 optimal policy를 찾을 수 있습니다.
즉 Policy Iteration이라는 것은 앞서 말했듯 두 가지 스텝으로 진행됩니다.
- Policy Evaluation을 통한 value function의 업데이트
- Policy improvement를 통해 더 나은 policy를 찾기
그럼 여기서 의문이 생깁니다.
단순히 greedy하게 policy를 update한다고 이전 policy보다 더 나은 Policy가 되는가?
deterministic policy $a = \pi(s)$를 생각해봅시다.
그리디를 통해 정책을 발전시킬 수 있습니다.
- $\pi’(s)=argmax$ $q_\pi(s,a)$
- $q_\pi(s,\pi’(s))= max$ $q_\pi(s,a)\geq q_\pi(s,\pi(s))=v_\pi(s)$
첫 번째 항은 첫 스텝에서만 $\pi’$을 따라 가고 그 뒤로는 $\pi$를 따르는 value 입니다.
뒤의 q에 대한 함수는 첫 스텝과 그 뒤도 $\pi$를 따라가는 value입니다.
우리는 업데이트를 통해 value가 계속 바뀔것이고, 그 상황에서 첫 번째 action이 최적인 경우는 그리디하게 선택하는 것과 동일하게 볼 수 있습니다.
그러므로 중간에 큐함수를 최대화하는 행동은 greedy하게 선택한 액션과 동일할 것이고 모든 식을 만족하게 됩니다.
계속 $\pi’$이 $\pi$보다 좋다가 어느 순간 같아지면 optimal policy!
강의 뒷편에 이게 local optimal에 빠지지 않고 global optimal에 무조건 수렴한다고 하는데 이 얘기는 왜그런지 잘 모르겠다.. :(
Value iteration
정책 이터레이션은 명시적인 정책이 존재하며, 그 정책을 평가하는 도구로서 가치함수를 사용합니다.
정책의 형태는 여러가지가 될 수 있으며 가치함수로 평가하는 정책은 이터레이션을 반복할수록 최적의 정책에 도달해갑니다.
이런 형태에서 정책과 가치함수는 명확히 분리돼있습니다.
정책이 독립적이므로 결정적인 정책(하나의 상태에서 하나의 행동만 선택)이 아니라 어떤 정책도 가능합니다. 대다수의 정책은 확률 정책입니다.(우리가 위에서 봤던 예시들) 이런 확률 정책을 사용하기 때문에 가치함수를 계산하는데 기댓값이 들어갈 수 밖에 없고, 따라서 정책 이터레이션에서는 벨만 기대 방정식을 사용했습니다.
하지만 만약 정책이 결정적인 형태로만 정의되면 어떨까요? 앞서 최적의 정책은 결정적이라고 말했습니다.
현재의 가치함수가 최적 가치함수는 아니지만 그렇다고 가정하고, 그 가치함수에 대해 결정적인 형태의 정책을 적용한다면 어떨까요?
말이 안된다고 느낄 수 있습니다.
처음 가치함수가 최적의 가치함수가 아니더라도, 반복적으로 가치함수를 발전시켜서 최적에 도달한다면 전혀 문제가 되지 않습니다. 실제로 이런 식으로 계산을 하면 최적 가치함수에 도달하고 최적 정책을 구할 수 있습니다.
정책 이터레이션과의 차이 점은 가치함수 안에 내재적으로 정책이 표현되어 있고 가치함수를 업데이트하면 정책 또한 같이 발전됩니다.
정리해봅시다.
벨만 기대 방정식을 통해 전체 문제를 풀어서 나오는 답은 현재 정책을 따라 갔을 때 받을 참 보상입니다.
- 가치함수를 현재 정책에 대한 가치함수라고 가정하고
- 반복적으로 계산합니다.(평가)
- 이러면 결국 현재 정책에 대한 참 가치함수가 된다는 것입니다.
벨만 최적 방정식을 통해 전체 문제를 풀어서 나오는 답은 최적 가치함수 입니다.
- 가치함수를 최적 정책에 대한 가치함수라고 가정하고
- 반복적으로 계산합니다.
- 결국 최적 정책에 대한 참 가치함수, 즉 최적 가치함수를 찾게 됩니다.
따라서 벨만 최적 방정식을 통해 문제를 푸는 가치 이터레이션에서는 따로 정책 발전이 필요 없습니다.
최적 정책을 가정했기 때문에 한 번의 정책 평가과정을 거치면 최적 가치함수와 최적 정책이 구해지고 MDP가 풀립니다.
\[v_*(s) = \max\limits_{a}(R_{t+1} + \gamma v_{*}(S_{t+1})\vert S_t=s,A_t=a)\]벨만 최적 방정식은 기대 방정식과 달리 max가 붙습니다. 따라서 새로운 가치함수를 업데이트할 때 정책의 값을 고려해줄 필요가 없습니다. 그저 현재 상태에서 가능한 $R_{t+1}+\gamma v_k(S_{t+1})$의 값들 중 최고의 값으로 업데이트하면 됩니다. 이를 가치 이터레이션이라고 합니다.
예시를 들어 봅시다.
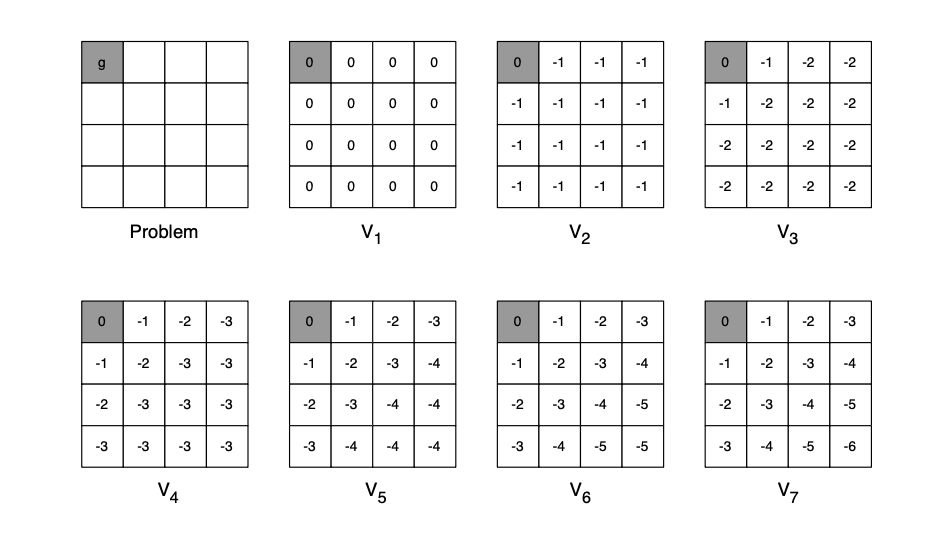
policy가 없고 step이 지날 때 마다 value function이 업데이트 됩니다.
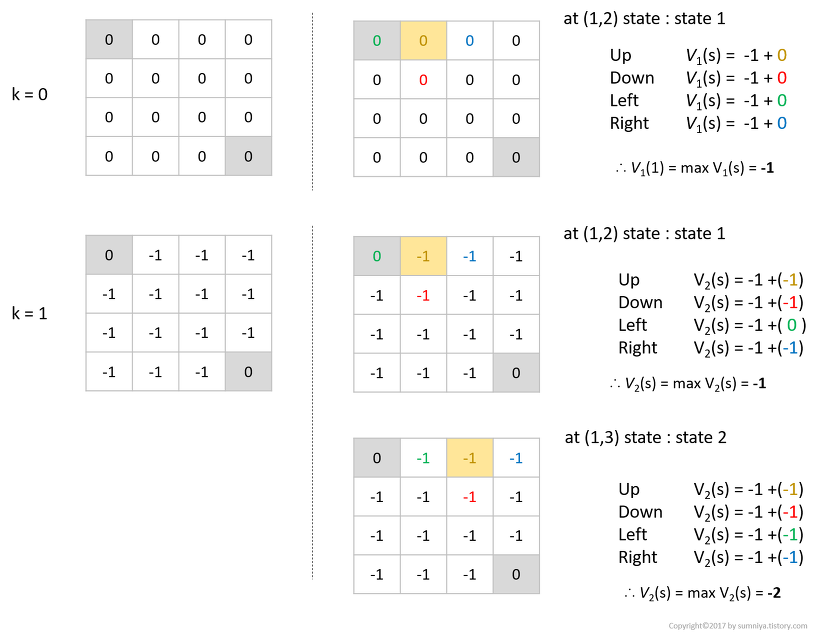
- $k=0$에서 각각의 상태에 대해 가치함수를 계산하면 모두 $-1$로 업데이트 됩니다.
- $k=1$에서 노란색 상태의 가치함수는 여전히 $-1$입니다.( 최대 값이 왼쪽으로 갈 때 $-1$이고 나머진 $-2$)

Comments