Model Evaluation
29 Jul 2020 | evaluation모델 평가 과정에서 문제 유형에 따라 서로 다른 지표를 사용하여 평가를 진행합니다.
하지만 대부분의 평가 지표는 단편적인 부분만을 반영합니다.
머신러닝에서 자주 사용되는 여러 평가 지표를 알아봅시다.
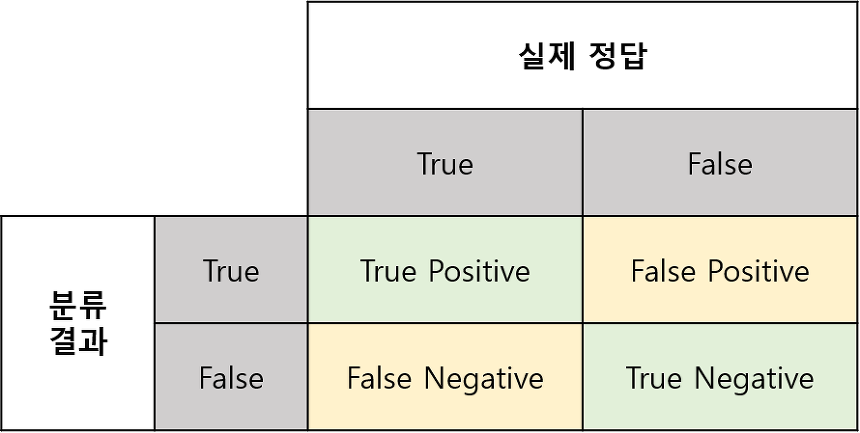
- True Positive : 모델이 날씨가 맑다고 했고 실제로 맑은 경우
- False Positive : 모델이 날씨가 맑다고 했고 실제로 흐린 경우
- False Negative : 모델이 흐리다고 예측했고 실제로 맑은 경우
- True Negative : 모델이 흐리다고 에측했고 실제로 흐린 경우
Precision
아주 간단한 예시를 들어봅시다. 일주일 간의 날씨 데이터가 있을 때 이를 예측하는 모델을 만들었습니다. 이 때 날씨는 맑거나 흐린 두 가지 경우만 있다고 가정합니다.
| Mon | Tue | Wed | Thu | Fri | Sat | Sun | |
|---|---|---|---|---|---|---|---|
| GT | ☀️ | ☀️ | ☁️ | ☀️ | ☀️ | ☁️ | ☀️ |
| Predict | ☀️ | ☀️ | ☀️ | ☀️ | ☁️ | ☁️ | ☁️ |
위 데이터를 가지고 confusion matrix를 채워봅시다.
| True | False | |
|---|---|---|
| True | 3 | 1 |
| False | 2 | 1 |
Precision은 모델이 True라고 예측한 값 중 실제로 True인 데이터의 비율입니다.
식으로는 다음과 같이 나타냅니다.
\[\frac{TruePositive}{TruePositive + FalsePositive}\tag{1}\]실제로 날씨가 맑은 날은 4일이고, 모델의 맑은 날 예측은 3일이므로 Precision은 3/4 입니다.
Recall
Recall은 실제 True인 데이터 중 모델이 True라고 커버하는 범위를 뜻합니다.
우리의 예시에서는 실제로 맑은 날일 때 모델이 맑은 날이라고 예측한 비율입니다.
식으로는 다음과 같이 나타냅니다.
\[\frac{True Positive}{True Postivie+False Negative}\tag{2}\]실제로 날씨가 맑은 날은 5일이고, 그 중 모델은 맑은 날이 3일이라고 예측 했으므로 Recall은 3/5 입니다.
사실 여기서 눈치채신분들도 있겠지만, Precision과 Recall은 Trade-off관계입니다.
한쪽 값으로 모두 예측해버리면 Recall이 높아지지만 Precision은 낮아집니다.
반대로 Precision을 높이면 Recall이 낮아집니다. 그래서 둘 사이의 적절한 균형을 찾는게 중요합니다.
Precision과 Recall 모두 TP를 높이면 성능이 높아집니다.
이를 위해 데이터에 많이 나타나는 클래스로 모두 예측한다고 가정해봅시다.(맑은 날이 많으면 모두 맑다고 예측).
이러면 확실히 TP는 올라가지만, TN의 파이가 작아집니다. 그로 인해 FN의 파이 또한 작아집니다. 그러므로 Recall이 확실이 높아질 순 있습니다. 그런데 Precision의 경우 기존보다 FP가 커지기 때문에 성능이 줄어듭니다.
F1 Score
F1 Score는 Precision과 Recall의 조화 평균입니다.
식으로는 다음과 같이 나타냅니다.
\[\frac{2\times Precision\times Recall}{Precision + Recall} \tag{3}\]조화 평균을 통해 Precision과 Recall사이의 작은 값에 대한 가중치를 고려한 평균 값을 찾을 수 있습니다.
산술, 기하 평균이 아닌 조화평균을 사용하면 더 작은 값에 대해 높은 가중치가 부여되어서 더 작은값쪽에 가까운 평균이 잡힙니다.(산술평균의 역수)
Accuracy
그렇다면 Negative sample에 대한 평가는 어떻게 이뤄져야 할까요?
날씨가 흐린 경우를 흐리다고 예측하는 것 또한 True case입니다.
이런 경우를 고려하는 평가 방식이 Accuracy입니다.
식으로는 다음과 같이 나타냅니다.
\[\frac{TruePositive + TrueNegative}{TruePositive+FalseNeagative+FalsePositive+TrueNegative} \tag{3}\]어려워 보이지만 모델이 True라고 잘 예측한 집합을 모든 데이터 집합으로 나눈 비율입니다. 말 그대로 Accuracy 입니다.
하지만 모든 데이터에 대해 모든 True case를 고려한다고 완벽한 평가지표가 될 수는 없습니다.
예를 들어, 아프리카의 날씨를 예측하는 모델이 있는데 눈이 오는 경우를 모두 False로 예측해버리면 정확도가 1에 수렴하겠죠? 이런 예시 처럼 클래스 별로 샘플 비율이 불균형한 경우 Accuracy는 불균형한 데이터의 영향을 많이 받습니다.
Fall-out
이 때 까지 정답인 케이스에 대한 평가 지표만을 다뤘습니다. 그렇다면 오답인 케이스에 대한 평가는 어떻게 내려야 할까요?
Fall-out은 실제로 False인 데이터에 대해 모델이 True라고 예측한 비율입니다.
식으로는 다음과 같이 나타냅니다.
\[\frac{FalsePositive}{TrueNegative + FalsePositive}\tag{4}\]P-R curve
일반적인 랭킹 문제를 예로 들어 봅시다.
이 문제에서는 모델의 예측으로 얻은 결과에 대해 직접적으로 pos, neg를 판별하는 정해진 임계값이 없습니다. 대신, Top N으로 반환된 결과의 Precision과 Recall을 통해 랭킹 모델의 성능을 평가합니다.
만약 유저에게 관련없는 컨텐츠가 계속 뜬다면, 이는 모델이 관련성 있는 컨텐츠를 충분히 찾아 주지 못했다는 것을 뜻하고, 이는 Recall이 낮다는 뜻입니다.
종합적으로 랭킹 모델을 평가하기 위해서는 서로 다른 Top N에서 Precision@N, Recall@N을 고려해야 하는데, 가장 좋은 방법은 P-R 곡선을 그려 보는 것입니다.
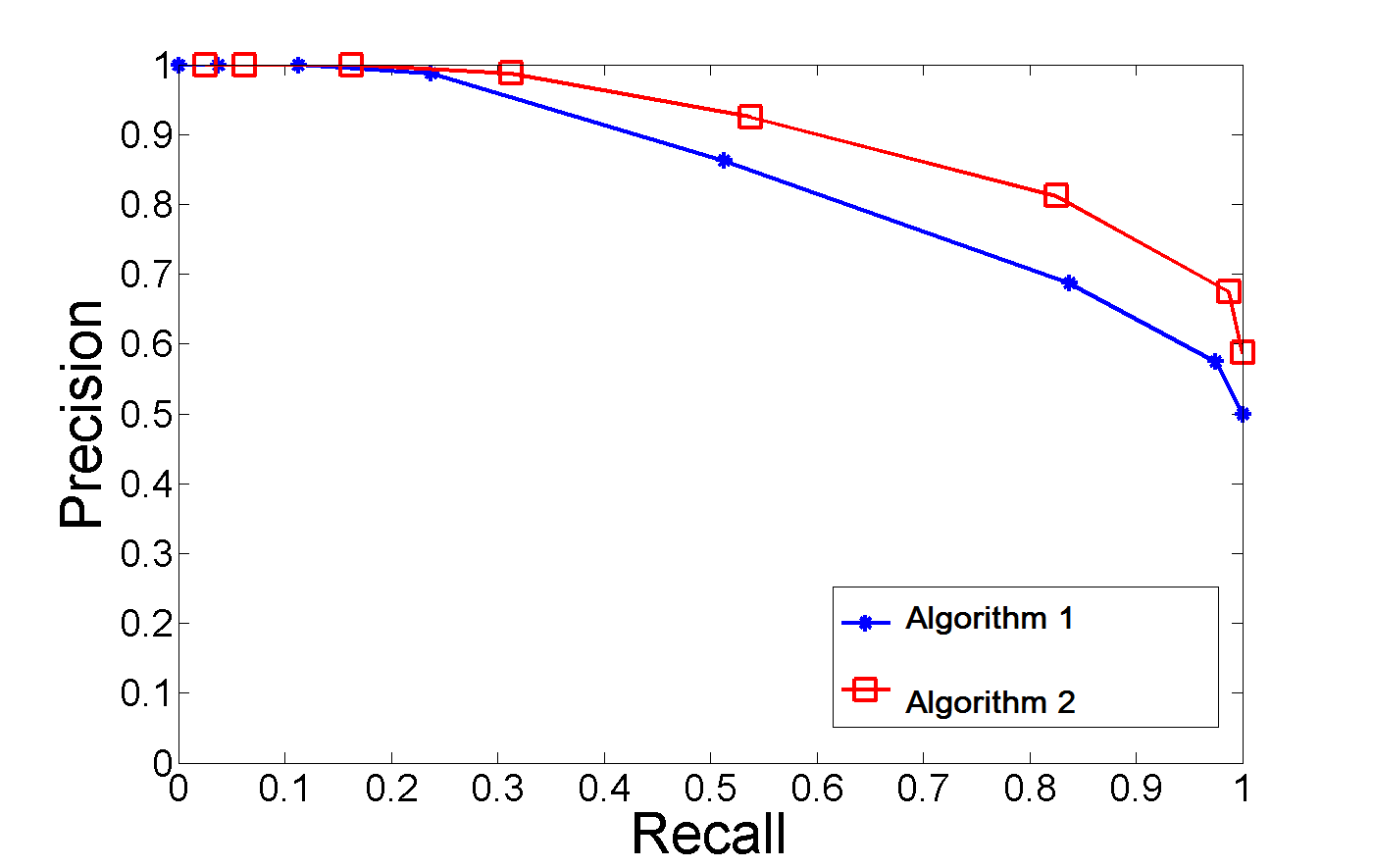
이를 통해 알 수 있는 점은 Precision과 Recall등 단편적인 평가 지표 만으로는 모델의 성능을 평가하기 힘들다는 것입니다. P-R 곡선의 전체적인 표현을 확인해야 모델에 대한 전면적인 평가가 가능합니다.
ROC curve
그렇다면 P-R curve처럼 False인 경우를 포함해서 두 가지 평가 지표를 동시에 고려하는 방법은 없을까요?
ROC curve는 x축엔 Fall-out(False-Positive rate), y축엔 Recall(True-Positive rate)를 사용한 그림입니다.
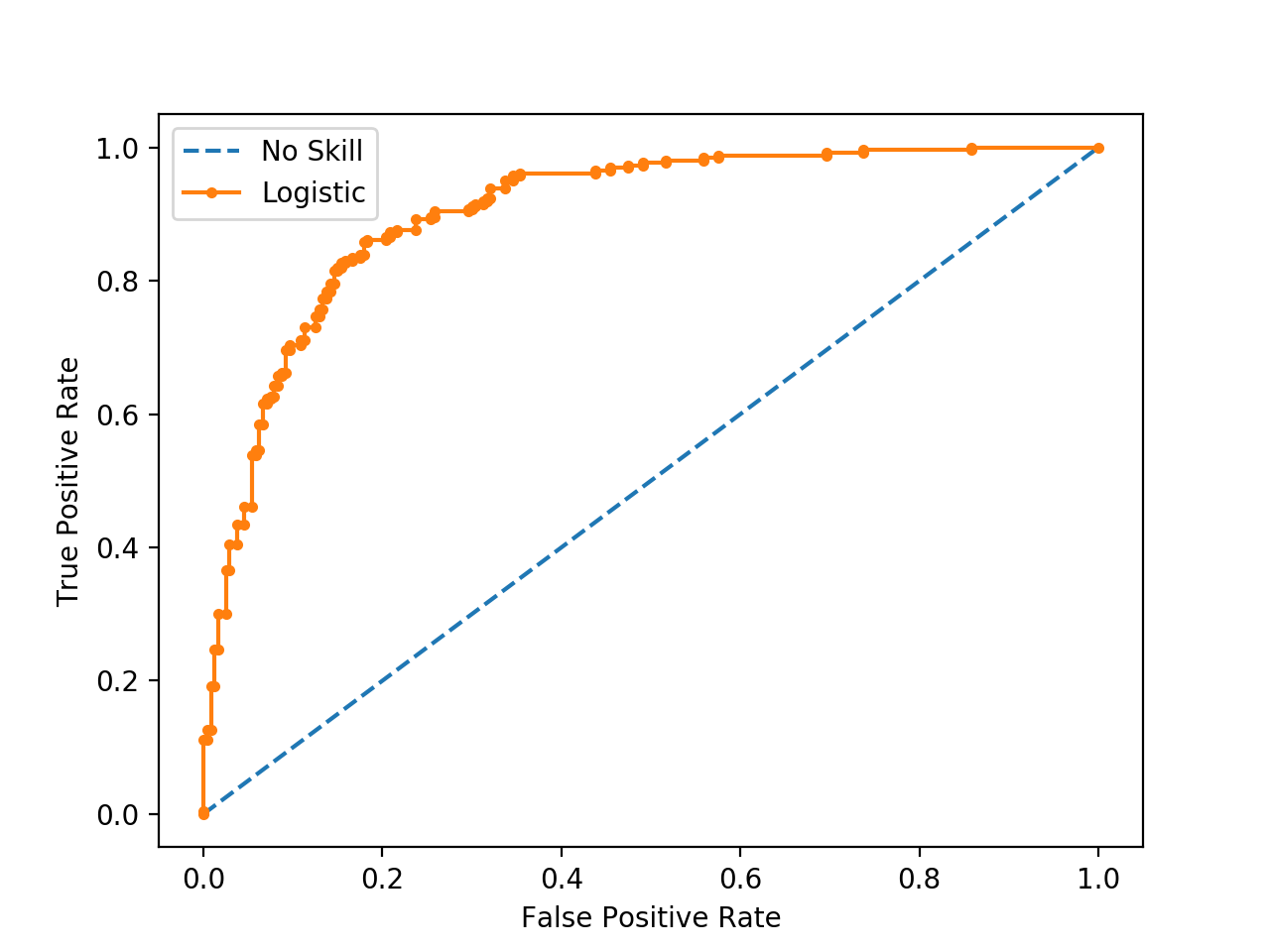
Curve의 면적이 1에 가까울수록 좋다는 것을 알 수 있습니다.
즉, Recall은 커야하고, Fall-out은 작아야 합니다.
여기서 한 가지 생각해 볼 점이 있습니다. Recall을 극단적으로 올리면 Fall-out은 어떻게 될까요?
날씨가 맑은 날에 대한 Recall을 높이는 방법은 극단적으로 모든 경우에 대해 맑다고 예측하는 것입니다.
그런데 이렇게 되면 Fall-out 또한 1로 수렴하게 됩니다.(모든 흐린날에 대해 맑다고 예측했으니까요) 즉, Recall(TPR)과 Fall-out(FPR)은 비례관계에 있습니다.
따라서 우리는 모델을 튜닝할 때 특정 기준(threshold)를 잘 설정해서 바꿔 가면서 Recall과 FPR을 측정해야 합니다.
AUC
AUC(Area Under Curve)는 ROC curve 아래의 면적을 뜻합니다.
앞서 말했듯, ROC의 면적이 1에 가까울수록 좋은 성능이라고 말씀드렸습니다. 이 지표를 통해 ROC curve에 기반해 모델 성능을 정량화하여 나타낼 수 있습니다.
ROC curve를 x축에 대해 적분하면 넓이를 구할 수 있습니다. 대부분의 ROC curve는 y=x위에 있기 때문에 일반적으로 AUC의 값은 0.5~1 사이의 값이 됩니다.
만약 ROC curve가 y=x아래에 있다면 모델의 예측 확률을 뒤집으면 더 좋은 성능의 모델을 얻을 수 있습니다.
Conclusion
우리는 각각의 모델을 단편적으로 평가하는 여러 방법들과 그 방법들을 결합한 P-R curve, ROC curve를 알아봤습니다.
마지막으로 P-R curve와 ROC curve를 비교해봅시다.
일반적으로 ROC curve는 postive, negative sample의 분포에 변화가 생겼을 때 기본적으로 변하지 않고 유지됩니다. 하지만, P-R curve는 급격한 변화를 보입니다.
만약 위의 날씨 데이터에서 Negative sample이 10배 늘어나면 어떻게 될까요?
FP와 TN의 파이가 엄청나게 커지고 이는 Precision을 낮추게 될 것 이고, 이는 P-R curve에서 y축이 낮은쪽으로 그래프가 형성될 것 입니다.
즉, ROC curve가 일반적으로 P-R curve 보다 다양한 테스트 세트를 만날 때 더 견고한 결과를 보여줍니다.
그런데 여기서 생각해볼 수 있는 점은, 불균형한 데이터 셋에 ROC curve를 사용해도 어느정도 예쁜 그래프를 보여준다는 말은 이런 케이스에서 ROC curve만 보고 모델을 평가하는게 굉장히 위험할 수 있을 것 같습니다. 오히려 불균형한 클래스 분포를 가진 데이터 셋에 대한 모델의 객관적인 성능 지표를 볼 때는 P-R curve가 나을지도..?
위의 예시 처럼 랭킹 모델을 얘기해보면 현실에서는 데이터의 positive, negative 비율이 굉장히 불균형합니다. 광고 영역에서 자주 사용되는 전환율 예측 모델에서 positive sample은 negative에 비해 굉장히 적습니다. 1/1,000 심지어 1/10,000인 경우도 많습니다.
ROC curve는 안정적으로 모델 자체의 성능을 반영할 수 있습니다.
하지만 주의해야 할 것은 P-R curve, ROC curve를 선택하느냐에 대한 문제는 해결하고자 하는 문제에 따라 달라집니다. 만약 모델이 특정 데이터 셋에서 어떤 성능을 내는지 알고 싶다면, P-R curve를 선택하는 것이 더 좋을 수도 있습니다.

Comments