sigmoid와 softmax의 차이점
26 Jul 2020 | Aisigmoid와 softmax의 차이점이 뭐에요?
단톡방에서 이 질문을 들었을 때 softmax는 확률 아웃풋이에요~ 라는 말 밖에 나오지 않았다.
생각해보니까 sigmoid도, softmax도 [0,1]사이의 값을 갖는 함수가 아니던가?
너무 기초적인 내용인데 이런 것도 제대로 대답하지 못해서 부끄러웠다.
그래서 오랜만에 기초적인 내용을 정리해보려한다.
일단 기본적으로 sigmoid가 어떻게 생겼는지 보고 가자.
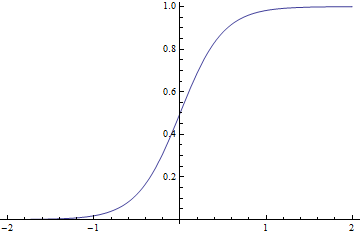
인공지능을 공부하면서 수 십번도 더 봤을 함수이다.
수식으론 다음과 같이 나타낸다.
\[sigmoid = \frac1{1+e^{-x}} \tag{1}\]softmax는 어떻게 생겼을까?
softmax는 일반적으로 각 인풋에 대해 정규화를 거친 뒤 확률값으로 아웃풋을 뱉어내는 함수이다.(따라서 인풋에 영향을 받기 때문에 일반화된 그래프는 보기 힘들다.)
수식으론 다음과 같이 나타낸다.
\[softmax = \frac{e^z_i}{\sum\limits_{j=1}^K e^{\beta z_j}} \tag{2}\]얼핏 봐서는 지수함수 형태의 변형이라는 것 말고는 비슷한 점을 잘 모르겠다.
한번 자세히 살펴보자.
우선 공통점으론 둘다 [0,1]사이의 값을 뱉어낸다는 것이다. 시그모이드의 경우 ‘S’형태의 커브를 띄는데, 통계에서 누적 분포 함수로도 쓰일 수 있고, 일반적으로 딥러닝에선 activation function으로 활용된다.(gradient vanishing은 TMI같으니까 여기선 언급 안하겠다.) 또한 둘다 ‘‘확률’‘로 해석할 수 있어서 분류 문제에 사용된다.
가장 큰 차이점은 softmax는 모든 [0,1]사이의 값을 다 더하면 1(확률)이 되지만 sigmoid는 모든 합(확률의 총 합)이 1이되진 않습니다. 그 말은 softmax의 output은 값 자체가 확률의 의미를 갖지만 sigmoid의 output은 그 클래스에 해당할 가능성을 나타낼 뿐 실제 확률값은 아니다.
결론부터 말하면 분류 문제에서 sigmoid의 일반화 버전을 softmax라고 얘기 할 수 있다.
그 예를 위해 binary case에 대해 두 함수를 전개해보자.
일반적인 logistic regression에서 특정 클래스{0,1}에 할당될 확률을 sigmoid를 통해 다음과 같이 나타낼 수 있다.
\[p(Y=1\vert X=\mathbf x) = \frac{1}{1+e^{-\beta^T \mathbf x}} \tag{3}\]softmax는 다음과 같다.
\[P(Y=K\vert X=\mathbf x) = \frac{exp(\beta^T_{Y_k})}{\sum_jexp(\beta^T_j \mathbf x)}\tag{4}\]이제 이 softmax식을 binary case에 대해 전개해보자.
\[p(Y=1\vert X=\mathbf x) = \frac1{\sum_{i=0}^1exp-(\beta_{Y_k}-\beta_j)^T\mathbf x}\] \[=\frac{1}{1+exp-(\beta_{Y_k}-\beta_j)^T\mathbf x}\] \[=\frac{1}{1+exp(-\beta^T)\mathbf x}\]이렇게 똑같은걸 볼 수 있다.

Comments