Logistic Regression

갑자기 로지스틱 회귀를 정리하게 될 일이 생겨서 정리하게 됐습니다.

유명하신 Ratsgo님과 Lovit님 블로그를 보고 정리했습니다.

두 블로그의 내용을 그대로 옮긴것과 다름 없기 때문에 아래의 출처에서 자세히 보시길 바랍니다.

로지스틱 회귀는 카테고리 변수를 예측하는 모델 입니다.

기존의 선형 회귀는 설명 변수 X와 연속형 숫자로 이뤄진 종속 변수 Y간의 관계를 Linear로 가정하고 이를 잘 표현하는 회귀계수를 데이터로부터 추정하는 모델입니다.

회귀계수는 모델의 Predict와 실제 값의 차이를 (보통 오차 제곱 합을 많이 사용함) 최소로 하는 값입니다.

이를 만족하는 최적의 계수는 회귀계수에 대해 미분한 식을 0으로 놓고 명시적인 해를 구합니다.(convex)

하지만 종속 변수 Y의 성질이 continuous가 아니라 categorical 이라면 어떨까요?

보시는 것 처럼 종속 변수가 카테고리형 변수이면 레이블의 값 자체가 의미를 가지지 않습니다.(레이블을 서로 바꿔도 별 의미가 없겠죠?)

이로 인해서 기존의 선형 회귀 모델을 그대로 사용할 수 없게 됩니다.

Sigmoid & Odds

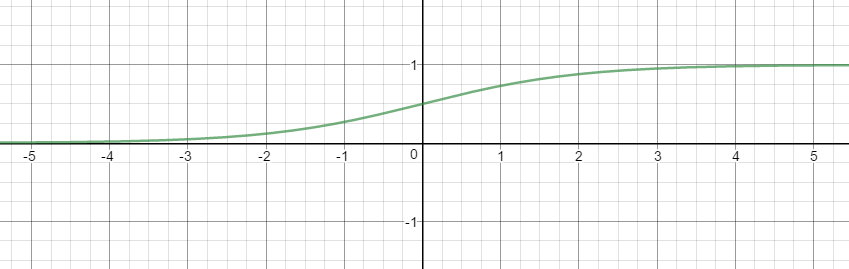
실제 세상에서는 특정 변수에 대한 확률 값이 선형이 아닌 S-커브 형태를 따르는 경우가 많다고 합니다.

이를 함수로 표현해낸 것이 시그모이드(로지스틱) 함수 입니다.

로지스틱 함수는 값으로 어떤 값이든 받을 수 있지만 출력 결과는 0~1입니다.

$y = \frac1{1+e^{-x}} \tag{1}$

Odds는 사건 A가 발생하지 않을 확률 대비 일어날 확률을 뜻하는 개념입니다.

$Odds = \frac{P(A)}{P(A^c)} \tag{2}$

왜 이런 얘기를 했을까요,

종속 변수가 카테고리형 일 때 각각의 레이블이 의미를 갖지 않는다고 말씀 드렸습니다.

그렇다면 각각의 레이블이 카테고리가 아니라 그 카테고리에 속할 확률이라고 생각해보는 것은 어떨까요?

그럼 문제를 다시 수식으로 풀어봅시다. (아래 식에서 우변은 일반적인 설명 변수로 표현한 회귀 식)

$P(Y=1\vert X=\mathbf x) = \beta_0 + \beta_1x_1 + \cdot\cdot\cdot + \beta_px_p = \mathbf \beta^T\mathbf x \tag{3}$

위 식의 좌변의 범위는 0~1 사이입니다.

하지만 좌변은 $(-\infty,\infty)$범위를 가지기 때문에 식이 성립하지 않는 경우가 존재합니다.

여기서 다시한번 식을 바꿔서 좌변을 Odds로 설정합니다.

$\frac{P(Y=1\vert X=\mathbf x)}{1-P(Y=1\vert x=\mathbf x)} = \beta^T\mathbf x \tag{4}$

하지만 이번에도 양 변의 범위가 맞지 않습니다.

Odds는 $(0,\infty)$의 범위를 갖습니다.

여기서 좌변에 로그를 취하는 기믹을 사용하면 양변의 범위가 맞춰집니다.

$log(\frac{P(Y=1\vert X=\mathbf x)}{1-P(Y=1\vert x=\mathbf x)}) = \beta^T\mathbf x \tag{4}$

이 식에서 회귀계수 벡터 $\beta$의 의미는 이렇습니다.

입력 벡터 $\mathbf x$의 첫번 째 요소인 $x_1$에 대응하는 회귀 계수 $\beta_1$이 학습 결과 2.5로 정해졌습니다.

그렇다면 $x_1$이 1 증가하면 레이블 “1”에 해당하는 로그 승산이 2.5 커집니다.

현재 가정은 레이블이 binary입니다. 레이블 = 0 or 1

위 식을 입력 벡터 $\mathbf x$가 주어졌을 때 레이블 “1”일 확률을 기준으로 정리해주면 다음과 같습니다.($x$가 주어졌을 때 레이블 1에 속할 확률을 $p(x)$, 위 식 우변을 a로 치환해서 정리)

$\frac{p(x)}{1-p(x)} = e^a$

$p(x) = e^a(1-p(x))$

$p(x)= e^a-e^ap(x)$

$p(x)(1+e^a) = e^a$

$p(x) = \frac1{1+e^{-a}}$

$p(Y=1\vert X=\mathbf x) = \frac1{1+e^{-\beta\mathbf x}}\tag{5}$

최종 도출 식이 sigmoid(logistic)와 비슷하죠?

그래서 로지스틱 회귀라는 이름이 붙었다고 합니다.

Geometric interpretation of logistic regression

바이너리 로지스틱 모델에 카테고리 정보를 모르는 입력 벡터 $\mathbf x$를 넣으면 범주 “1”에 속할 확률을 반환해준다고 했습니다.

그럼 그 확률값을 얼마나 되어야 “1”이라고 분류할 수 있을까요?

가장 간단한 방식은 아래와 같습니다.

$P(Y=1\vert X=\mathbf x) > P(Y=0\vert X=\mathbf x) \tag{6}$

레이블이 두 개 뿐이므로 아래와 같이 위 식을 정리할 수 있습니다.(위 식 좌변을 $p(x)$로 치환 )

$p(x)>1-p(x)$

$\frac{p(x)}{1-p(x)} >1$

$log(\frac{p(x)}{1-p(x)}) > 0$

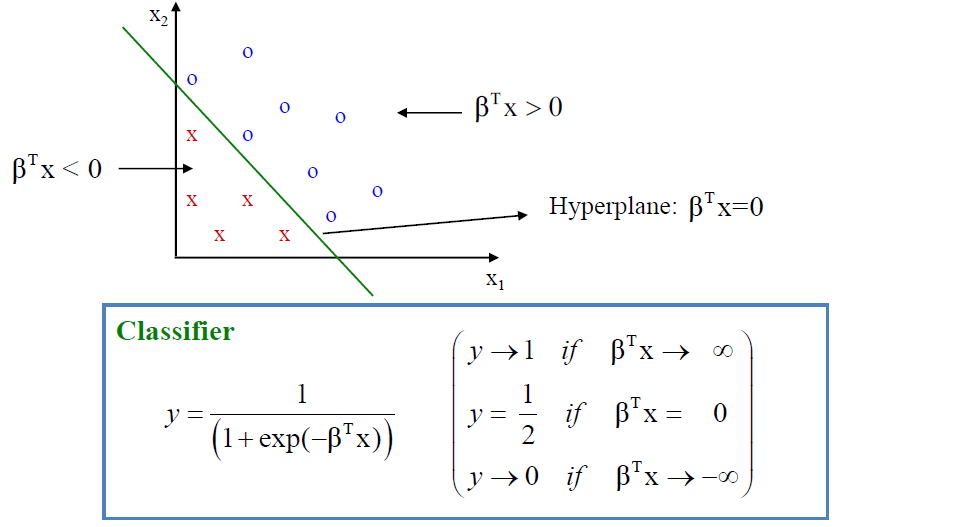
$\beta^T\mathbf x > 0$

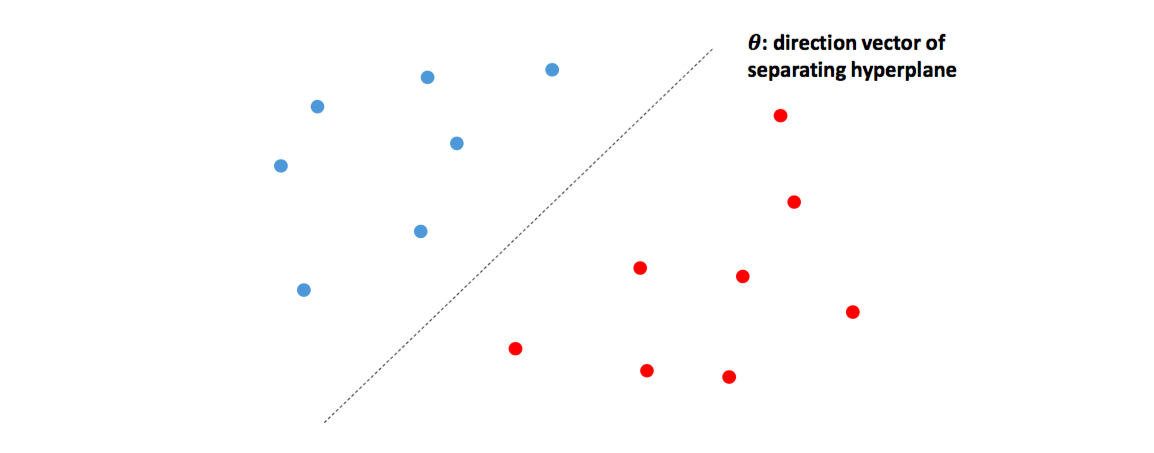
결국 로지스틱 회귀를 기하적으로 해석하면 $\beta^T \mathbf x$는 데이터가 분포된 공간을 나누는 결정 경계(decision boundary)입니다.

입력 벡터가 2차원인 경우 아래처럼 직선이 될테고 3차원이면 평면이 되겠죠?

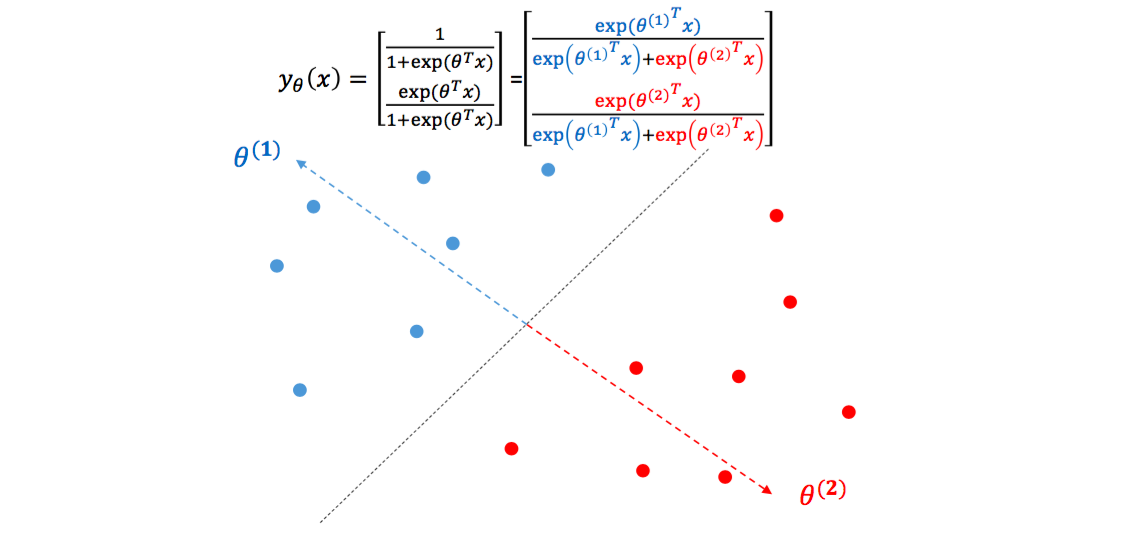
좀 더 들어가 봅시다 각각의 $\theta$는 일종의 클래스 대표 벡터가 됩니다.

$\theta_1$은 파란 점들의 대표 벡터, $\theta_2$는 빨간 점들의 대표 벡터입니다.

하나의 클래스당 하나의 대표 벡터를 가집니다.

만약 한 점 $x$가 $\theta_1$과 일치한다면, $e^{\theta^T_1x}$는 어느정도 큰 양수가, $e^{\theta^T_2x}$는 0에 가까운 값이 되기 때문에 $x$는 “1”에 해당할 확률이 1이 됩니다.

결론은 로지스틱 회귀는 각 점에 대하여 각 클래스 대표 벡터에 얼마나 가까운지를 학습하는 것입니다.

Reference

Ratsgo

Lovit