Word2Vec
02 Jul 2020 | NLPWord2Vec
토큰들을 확률로 나타내는 방법
직관적으로 생각해보자, 우리는 각각의 토큰들에 확률을 부여하기 위한 모델을 만들 필요가 있다.(언어 모델의 전통적인 접근 방식 관심이 있으면 아래의 링크를 살펴보자.)
좋은 언어 모델은 semantically & syntactivally 완전한 문장에 높은 확률을 부여할 것이다. 반대로 전혀 말이 안되는 문장에는 낮은 확률을 부여해야 한다.
수학적으로, n개의 단어로 이루어진 어떤 문장이라도 이런 확률을 부여할 수 있다.
\[P(w_1,w_2,....,w_n) \tag{1}\]단어들의 등장이 독립이라는 전제 하에 이런 확률들을 다음과 같이 분해할 수 있다.
\[P(w_1,w_2,...,w_n)=\prod_{i=1}^nP(w_i)\tag{2}\]사실 이건 굉장히 rough한 방법이다.
우리는 직관적으로 이전의 단어들의 묶음과 이후에 나올 단어의 상관관계가 매우 높은 것을 알 수 있다.
따라서 우리는 문장의 확률이 문장의 묶음과 이후에 나오는 단어 쌍의 확률에 의존하도록 하고 싶은 것이다.
이러한 방법을 biagram model이라고 부르고 다음과 같이 나타낸다.
\[P(w_1,w_2,...,w_n)=\prod_{i=2}^nP(w_i\vert w_{i-1})\tag{3}\]하지만 여전히 이 방법 또한 naive하다. 오직 이웃한 단어의 쌍만 고려하기 때문이다.
하지만 이런 표현은 우리가 모델링을 어느정도 진행했음을 보여준다.
컨텍스트의 크기를 1로한 word-word matrix를 이용해서, 이런 단어 쌍의 확률을 기초적으로 학습할 수 있다. 하지만 이런 방법은 또 다시 대규모 데이터 셋에 대한 global information을 계산하고 저장하는 과정이 필요하다.
Word2vec
word2vec의 특징은 input, hidden, output 3가지 레이어로도 워드 임베딩이 가능하다는 점이다.
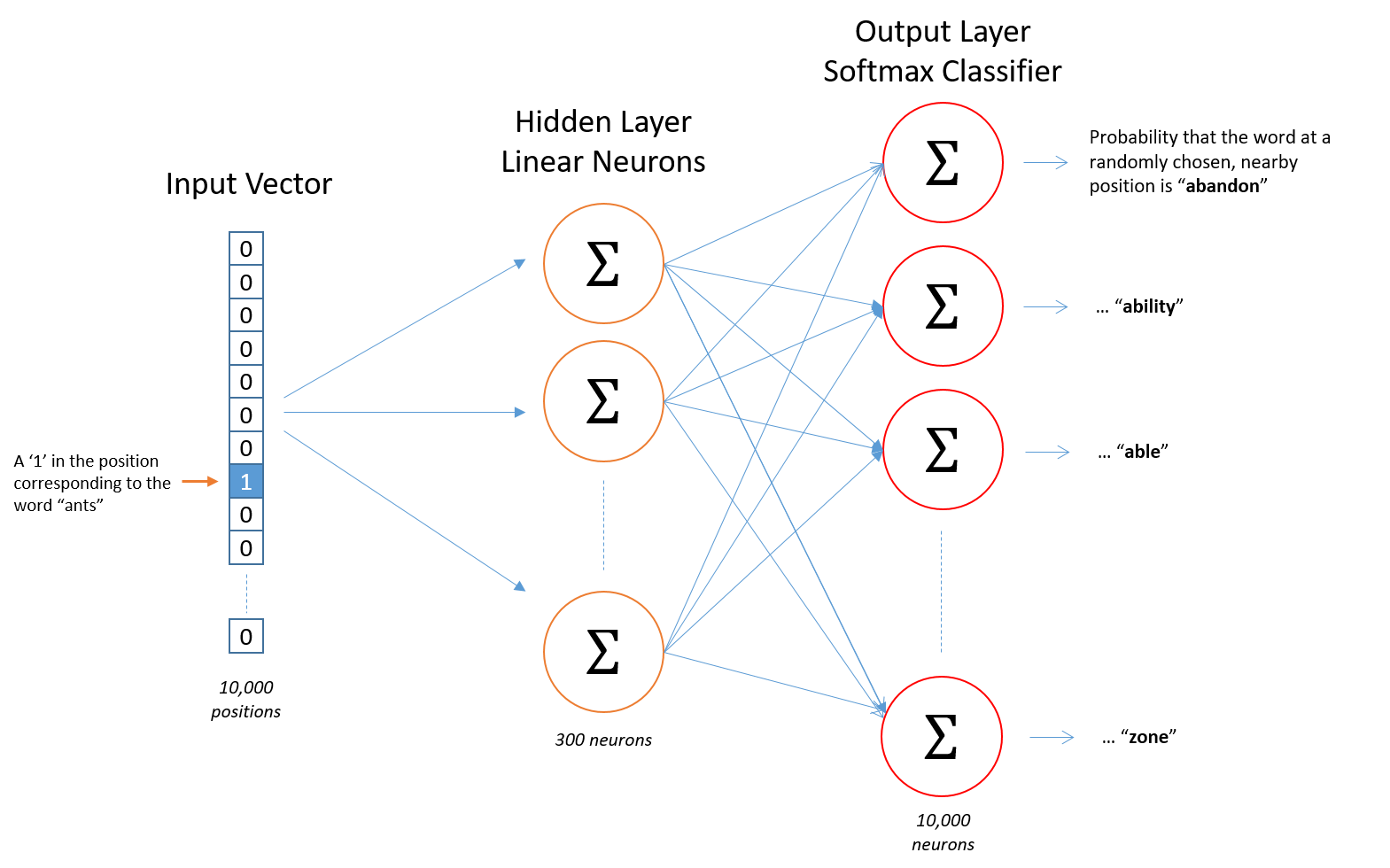
재밌는 사실은 인풋이 one-hot이기 때문에 W의 shape은 (input,hidden)이 될텐데 이 Weight 자체가 바로 word vector가 된다는 점이다.

학습된 파라미터 자체를 사용하기 때문에 lookup table처럼 사용 가능하고 word vector의 feature를 자신에 맞게 조절할 수 있다.
그렇지만 학습 완료된 모델에 새로운 단어를 인풋으로 사용할 수는 없다.
마치 이런점이 collaborative filtering의 새로운 유저에게 추천을 하지 못해주는 cold start와 같다.
애초에 유사도를 기반으로 분류해야하니까 cf기반 방식에 분류되는게 납득이 간다.
Skip-Gram Model
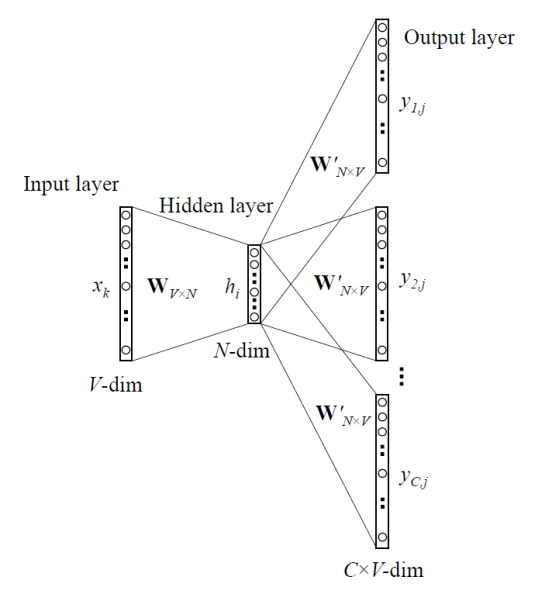
word2vec은 모델 구조에 따라 2가지로 나눌 수 있는데 CBOW와 Skip-Gram형식이다.
우린 그 중에서 성능이 더 좋다고 알려진 (위 그림) Skip-Gram형식에 대해서만 다뤄 보자.
Skip-Gram은 중심 단어를 통해 주변 단어를 예측한다.
즉, 주어진 중심 단어 “Jumped”를 이용해서 주변의 연관된 단어 “The”, “Cat”, “over”, “the”, “puddle”을 예측하는 것이다. 여기서 우리는 중심 단어 “Jumped”를 context 라고 부른다.
SKip-Gram의 학습 과정을 살펴보자.
- 중심 단어를 one-hot vector로 만들어 준다.
- $\mathbf W_{V \times N}$를 곱해줘서 embedded vector를 구한다.
- embedded vector에 $\mathbf W’$를 곱해서 scroe vector를 계산한다.
- 위에서 구한 각 score vector에 대해서 확률 값으로 만들어 준다.
Skip-Gram모델의 겨우 context의 주변 단어 모두를 예측하기 때문에 확률 값이 2m개가 나온다.
\[\hat y_{c-m},...,\hat y_{c-1},\hat y_{c+1},...,\hat y_{c+m}\tag{8}\]이제 구한 확률 값에 대해서 각 위치의 정답과 비교한다.
\[\hat y^{c-m},...,\hat y^{c-1},\hat y^{c+1},...,\hat y^{c+m}\tag{9}\]Object function
학습을 위해 Objective function을 다음과 같이 정의하고 최소화 한다.
CBOW와의 차이점은 각 단어에 대해 독립적이라고 가정하는 것이다.
다시 말해서 중심 단어에 대해서 모든 output 단어들은 완전히 독립적이다.(independent)
\[minimize J = -logP(w_{c-m},...,w_{c-1},w_{c+1},...,w_{c+m}\vert w_c)\tag{10}\] \[= -log \prod_{j=0,j \neq m}^{2m} P(w_{c-m+j} \vert w_c)\tag{11}\] \[= -log \prod_{j=0,j \neq m}^{2m} \frac{exp(u^T_{c-m+j}v_c)}{\sum_{k=1}^{\vert V\vert} exp(u^T_k v_c)}\tag{12}\] \[= - \sum_{j=0,j\neq m}^{2m} u^T_{c-m+j} v_c + 2mlog\sum_{k=1}^{\vert V\vert} exp(u^T_k v_c)\tag{13}\]복잡해보이는 softmax에 대한 부분만 조금 가져와보면,
\[P(o\vert c) = \frac {exp(u^T_ov_c)}{\sum_{w=1}^W exp(u^T_wv_c)}\tag{14}\]표기가 조금 다르긴 하지만 위 식과 동일하게 생각할 수 있다.
우선 $v$는 input-hidden을 잇는 $W$의 행 벡터, $u$는 hidden-output을 잇는 $W’$의 열벡터 이다.
우변 분자의 지수를 키운다는 것은 중심 단어 $c$에 해당하는 벡터와 주변단어 $o$에 해당하는 벡터의 내적값을 높인다는 뜻.
벡터 내적은 코사인 이므로 내적값을 높이는 것은 word vector간의 유사도를 높인다는 의미로 해석할 수 있다.
분모는 반대로 작아질수록 좋은데,
그 의미는 윈도우 크기 내에 등장하지 않는 단어들은 중심 단어와의 유사도를 감소시킨다 라고 해석할 수 있다.
이 목적 함수와 함께 우리는 각 iteration마다 Unknown 파라미터 들에 대한 gradients를 계산할 수 있고, SGD를 통해 파라미터를 업데이트 한다.
\[J = -\sum_{j=0,j\neq m}^{2m} logP(u_{c-m+j}\vert v_c)\tag{15}\] \[= \sum_{j=0,j\neq m}^{2m} H(\hat y,y_{c-m+j})\tag{16}\]위 식에서 $H$는 probability vector $\hat y$와 one-hot vector $y_{c-m+j}$간의 cross entropy이다.
Subsampling Frequent words
Skip-Gram모델은 중심 단어에 대해서 주변 단어를 예측하며 Update하기 때문에 CBOW모델보다 각 단어에 대해서 update 기회가 더 많다(SkipGram모델을 CBOW보다 많이 쓰는 이유이기도 하다.). 아래 그림을 보면 Skip-Gram이 학습을 진행하는 과정에 대해서 볼 수 있다.
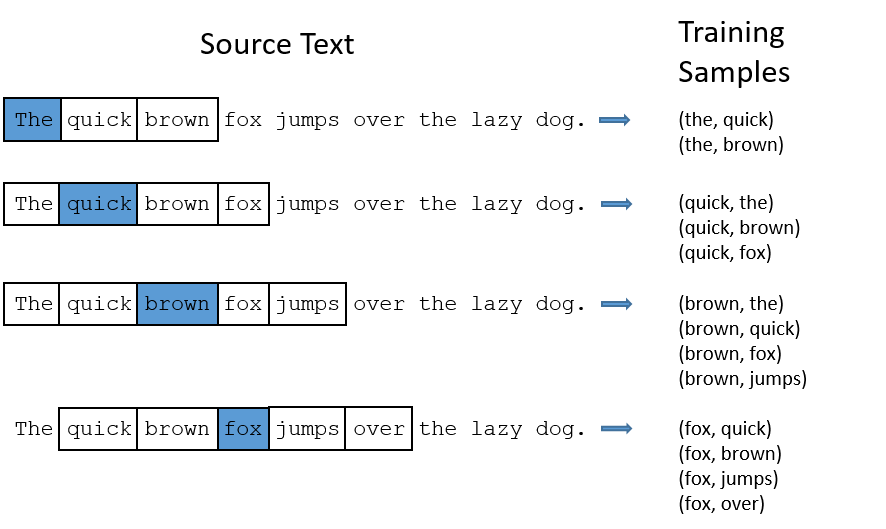
학습 과정을 보면 “the”와 다른 단어가 함께 training되는 경우가 많다는 것을 볼 수 있다.
이 그림은 한 문장에 대한 예시 이지만 전체 데이터에서 “the”라는 단어와 얼마나 많은 단어들이 매핑 될지 생각해보자. 단어의 특성상 데이터 안에서 매우 자주 등장할 것이고, 그 만큼 update되는 횟수도 많을 것이다. 하지만 “the”라는 단어는 그다지 의미적으로 중요하지는 않다.
이러한 경우 학습 시간만 증가시킬 뿐 학습 정확도에 크게 기여하지 않는다.
이런 문제를 해결하는 방법이 Subsampling Frequent words 이다.
Subsampling 방법은 학습 시에 단어들을 무작위로 제외 시키는 것이다.(보자마자 dropout 떠오름)
만약 자주 등장 하는 단어라면 더 자주 제외시켜야 한다.
단어별로 제외되는 확률은 다음과 같이 정의된다.
\[P(w_i) = 1 - \sqrt[2]\frac{t}{f(w_i)}\tag{17}\]위 식에서 $f()$는 각 단어의 전체 데이터에 출현하는 횟수이다.
즉 자주 등장하는 단어 일수록 확률 값이 줄어들게 된다. $t$는 하이퍼 파라미터로 논문에서는 $10^{-5}$를 추천한다.
Negative sampling
object function을 들여다 보기 위한 이전 단계로 넘어가 보자. $\vert V\vert$합을 계산하는 것은 계산량이 매우 많이 필요하다. ($\vert V\vert$는 전체 단어의 개수이다.)
이를 해결하기 위한 간단한 아이디어는 직접 계산하는 것이 아닌 근사 하는 방법이다.
매 training step마다 모든 단어에 접근하는 대신 몇몇의 부정적인 예제들(negative examples)을 샘플링 할 수 있다. 우리는 단어들의 빈도를 정렬한 noise distribution $(P_n(w))$으로 부터 “sample”할 수 있다.
즉 기존의 확률 계산에서는 모든 단어에 대해서 전체 경우를 구했지만, 여기서는 현재 window내에서 등장 하지 않는 단어를 특정 개수 만큼 뽑아서 확률을 계산하는 것이다.
예를 들면 window_size = 5 라면, window내에 등장 하지 않는 데이터 내의 다른 단어 5~25개 정도를 뽑아서 확률을 계산하는 것이다.
우리의 방법을 Negative sampling과 결합하기 위해서 필요한 일은 다음의 것들을 업데이트 하는 것이다.
- object function
- gradients
- update rules
Negative sampling이 Skip-Gram모델에 기반하고 있지만 사실 이는 다른 목적 함수를 최적화한다.
$(w,c)$의 단어와 컨텍스트 쌍을 고려해보자.
이 쌍이 트레이닝 데이터로 부터 왔는가?
$(w,c)$쌍이 코퍼스 데이터로 부터 추출 되었을 확률을 $P(D=1\vert w,c)$라고 표기하자.
반대로, 추출되지 않았을 확률은 $P(D=0\vert w,c)$로 표기할 수 있을 것이다.
첫 번째 확률을 시그모이드를 통해 모델링 해보자.
\[P(D=1\vert w,c,\theta) = \sigma(v^T_cv_w) = \frac1{1+e^{-v_c^Tv_w}}\tag{18}\]우리는 이제 word & context가 실제로 코퍼스 안에 존재하면 코퍼스에 있을 확률을 maximize하고, 코퍼스 안에 존재하지 않으면 코퍼스에 없을 확률을 maximize하는 새로운 object function을 만들면 된다.
우리는 이 두 확률에 대해 간단한 maximum likelihood 방법을 취할 수 있다.($\theta$를 모델의 파라미터로 설정할 것인데, 이 문제의 경우 이는 $V$와 $U$를 나타낸다.)
(이건 수식이 너무 길어서 생략.. reference에 달아 놓음)
likelihood 를 최대화 하는 문제는 전통적으로 머신러닝에서 $-log$를 붙여 최소화 하는 문제로 바꿀 수 있다.
\[J = -\sum_{(w,c)\in D}log\frac1{1+exp(-u^T_wv_c)} - \sum_{(w,c)\in \tilde D}log\frac1{1+exp(u^T_wv_c)}\tag{19}\]Skip-Gram에서 주어진 중심 단어 $c$로 부터 context 단어 $c-m+j$를 관찰하는 새로운 목적 함수는 다음과 같다.
\[-log\sigma(u^T_{c-m+j}\cdot v_c ) - \sum_{k=1}^Klog(-\tilde u^T_k \cdot v_c)\tag{20}\]위 수식에서 ${\tilde u_k \vert k=1,…,K}$는 $P_n(w)$로 부터 샘플링되었다.
이제 $P_n(w)$가 무엇인지 논의해보자.
무엇이 가장 좋은 근사인지에 대한 많은 논의가 있지만, 가장 좋아보이는 방법 3/4 제곱을 이용한 Unigram Modeldlek.
왜3/4? 이에 대한 직관적인 이해는 아래와 같다.
“is” : $0.9^{3/4} = 0.92$
“constitution” : $0.09^{3/4} = 0.16$
“bombastic” : $0.01^{3/4} = 0.032$
이제 “is”에 비해 “bombastic”은 3배 이상 자주 샘플링 될 것이다.
$P_n(w)$는 다음과 같이 표기할 수 있다.
\[P(w_i) = \frac{f(w_i)^{3/4}}{\sum_{j=0}^n(f(w_i)^{3/4})}\tag{21}\]
Comments